Определение окружности, круга. Радиус
Определение окружности, круга. Радиус
Окружность - геометрическое место точек плоскости, равноудаленных от одной ее точки (центра).
Равные отрезки, соединяющие центр с точками окружности, называются радиусами.
Круг - часть плоскости, лежащая внутри окружности.
Хорда, дуга, диаметр
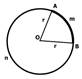
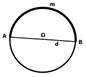
Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, - хордой. Хорда, проходящая через центр О, называется диаметром. Диаметр равен двум радиусам.
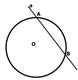
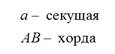
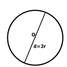
Часть окружности называется дугой.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
Касательная к окружности
Касательная - прямая, имеющая с окружностью только одну общую точку.
Теорема. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
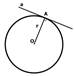
Обратная теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Окружность, описанная около треугольника
Определение. Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности.
При этом треугольник называется вписанным в окружность.
OA=OB=OC=R
Расстояние от любой вершины треугольника до центра описанной окружности равно радиусу этой окружности.
Окружность можно описать около любого треугольника.
Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника (то есть отрезков, перпендикулярных к сторонам треугольника и проходящих через середины этих сторон).
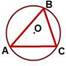
Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.
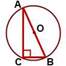
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
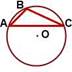
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника (напротив тупого угла, за большей стороной).
| Окружность, описанная около треугольника | ||
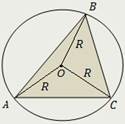 | Окружность называется описанной около треугольника, если она проходит через все его вершины. Радиус описанной окружности:  | |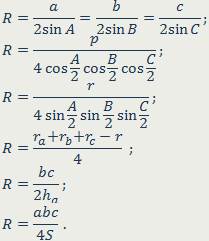
| Расположение центра описанной окружности | ||
 |  |  |
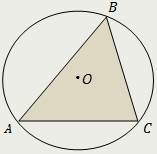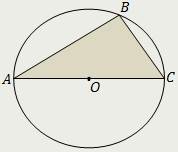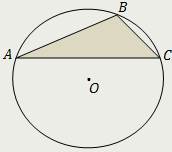| Центр описанной окружности остроугольного треугольника расположен внутри треугольника. | Центр описанной окружности прямоугольного треугольника совпадает с серединой его гипотенузы. | Центр описанной окружности тупоугольного треугольника расположен вне треугольника. |
Касательная к окружности
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.
| Окружность, вписанная в треугольник | |
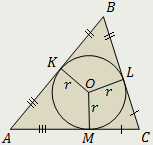 | Окружность называется вписанной в треугольник, если она касается всех его сторон. Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков: 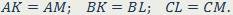 Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:  |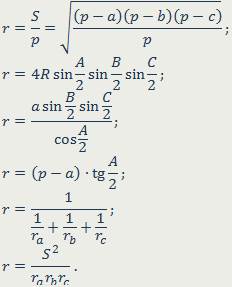
Вневписанная окружность
Ну вот, пора приступать к самому непонятному. Что же это за зверь такой: «вневписанная окружность»? Сначала посмотри на картинку:
Видишь, окружность тоже чего-то касается, но «сидит» как-то снаружи, вне треугольника? Вот поэтому и называется вневписанной.
| Окружность называется вневписанной для треугольника, если она касается ОДНОЙ стороны треугольника и продолжений двух других сторон. |
Касание окружностей
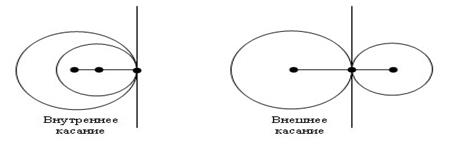
Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Через точку касания можно провести касательную к одной из окружностей, которая является одновременно и касательной к другой окружности. Касание окружностей бывает внутренним и внешним.
Касание называется внутренним, если центры окружностей лежат по одну сторону от касательной.
Касание называется внешним, если центры окружностей лежат по разные стороны от касательной
Углы, вписанные в круг
Угол разбивает плоскость на две части. Каждая из этих частей называется плоским углом. Плоские углы с общими сторонами называются доповняльними. Если плоский угол является частью полуплоскости, то его градусной мере, называется градусная мера обычного угла с теми же сторонами.
Центральным углом в окружности называется плоский угол с вершиной в центре круга.
Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу. Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, вершина которого лежит на окружности, а стороны пересекают это окружность, называется вписанным в окружность. Точки, в которых стороны вписанного угла пересекают окружность, разбивают окружность на две дуги. Центральный угол, что соответствует той из этих дуг, не содержит вершину угла, называется центральным углом, который соответствует данному вписанному углу.
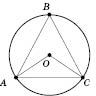
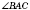- вписанный;
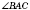- опирается на хорду BC;
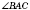- опирается на дугу BC;
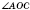- центральный угол, соответствующий вписанному углу АВС.
Рассмотрим, как находить их градусные меры.
Свойства вписанных углов
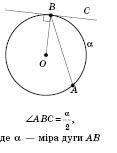
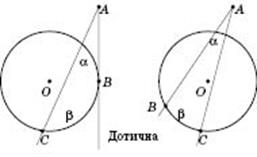
- Вписанный угол равен половине дуги, на которую он опирается.
- Вписанный угол равен половине центрального угла, опирающегося на ту же дугу:
- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на диаметр равен 90°.
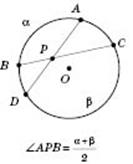
- Любая пара вписанных углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.
6. Центральный угол и вписанный угол
7. Угол с вершиной в центре окружности называется центральным углом.
8. Градусная мера центрального угла равна градусной мере соответствующей дуги окружности:
9. ∡AOB=∪AB.
10. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
11. Вписанный угол измеряется половиной дуги, на которую он опирается:
12. ∡ACB=12∪AB.
13. 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
14. 2. Вписанный угол, опирающийся на полуокружность, равен 90°.
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности: a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности: a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
| r = | a√3 |
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
| R = | a√3 |
5. Формула площади правильного треугольника через длину стороны:
| S = | a2√3 |
6. Формула площади правильного треугольника через радиус вписанной окружности: S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
| S = | R2 3√3 |
8. Угол между сторонами правильного треугольника: α = 60°
Правильный четырехугольнику - квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности: a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности: a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
| r = | a |
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
| R = | a√2 |
5. Формула площади правильного четырехугольника через длину стороны: S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности: S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности: S = 2 R2
8. Угол между сторонами правильного четырехугольника: α = 90°
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
| a = | 2√3 | r |
2. Формула стороны правильного шестиугольника через радиус описанной окружности: a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
| r = | a√3 |
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны: R = a
5. Формула площади правильного шестиугольника через длину стороны:
| S = | a2 3√3 |
6. Формула площади правильного шестиугольника через радиус вписанной окружности: S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
| S = | R2 3√3 |
8. Угол между сторонами правильного шестиугольника: α = 120°
Значение числа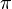
(произносится «пи») — математическая константа, равная отношению
длины окружности к длине её диаметра, оно выражается бесконечной десятичной дробью.
Обозначается буквой греческого алфавита «пи». Чему равно число пи? В простых случаях хватает знать первые 3 знака (3,14).
53. Найдем длину дуги окружности радиуса R, отвечающей центральному углу в n°
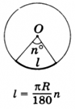
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.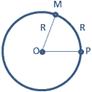 
Градусная мера угла в 1 радиан равна:
Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.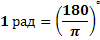 
И наоборот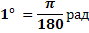 
Так как π = 3,14, то 1 рад = 57,3°
Если угол содержит a радиан, то его градусная мера равна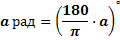 
И наоборот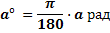 
Обычно при обозначении меры угла в радианах наименование «рад» опускают.
Например, 360° = 2π рад, пишут 360° = 2π
В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.
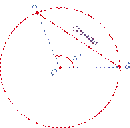
Круговой сегмент
Круговой сегмент - это часть круга, ограниченная дугой окружности и стягивающая ее хордой.
R - радиус круга;
a0 или a радиан - дуга сегмента (угол AOB).
Свойства сегмента
Свойство 1
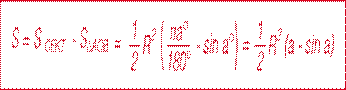
Свойство 2
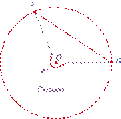
Свойство 3
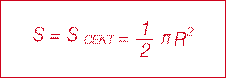
Прямая Эйлера это:
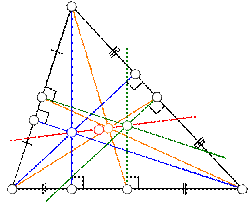
Прямая Эйлера (красная) проходит через центр описанной окружности треугольника, его ортоцентр, центр тяжести и центр окружности девяти точек
три высоты треугольника также пересекаются в одной точке, которая называется его ортоцентром.
Окружность Эйлера
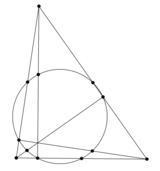
В геометрии треугольника окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника. Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек.
Окружность девяти точек получила такое название из-за следующей теоремы:
| Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности. |
Окружность девяти точек обладает ещё целым рядом свойств:
· Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.
· Радиус окружности девяти точек равен половине радиуса описанной окружности. Более того, описанная окружность есть образ окружности девяти точек относительно гомотетии с центром в ортоцентре и коэффициентом 2.
· (теорема Фейербаха) Окружность девяти точек произвольного треугольника касается вписанной и всех трёх вневписанных окружностей этого треугольника.
Окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника. Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек, окружностью Теркема, окружностью двенадцати точек, включая точки Фейербаха , окружностью n-точек, полуописанной окружностью.
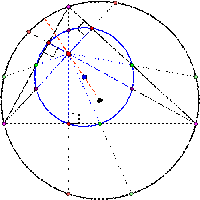
Треугольник, описанная вокруг него окружность (черная) и её центр (чёрный), высоты треугольника (часть высоты, расположенная внутри окружности Эйлера, синяя, а вне - её черная) и окружность девяти точек (синяя) и её центр (синий)
Окружность девяти точек получила такое название из-за следующей теоремы:
| Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности. |
Иначе говоря, окружность девяти точек является описанной окружностью для следующих трёх треугольников:
- ортотреугольник,
- дополнительный треугольник,
- треугольник Эйлера (или треугольник Фейербаха, треугольник Эйлера — Фейербаха) — треугольник, вершинами которого служат середины трёх отрезков, соединяющих ортоцентр и вершины.
Определение окружности, круга. Радиус
Окружность - геометрическое место точек плоскости, равноудаленных от одной ее точки (центра).
Равные отрезки, соединяющие центр с точками окружности, называются радиусами.
Круг - часть плоскости, лежащая внутри окружности.
Хорда, дуга, диаметр
Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, - хордой. Хорда, проходящая через центр О, называется диаметром. Диаметр равен двум радиусам.
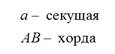
Часть окружности называется дугой.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
Касательная к окружности
Касательная - прямая, имеющая с окружностью только одну общую точку.
Теорема. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Обратная теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.