Решение прямой геодезической задачи на поверхности эллипсоида по формулам немецкого геодезиста Шрейбера

(выведены в 1878 г.)

Исходные данные: B₁, L₁, A_1,2, s (см. рис. 31).

Основные формулы:

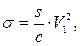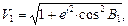
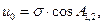
(128)

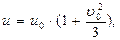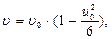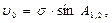
(129)

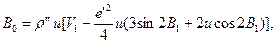
(130)

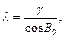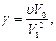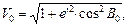(131)

- 59 -

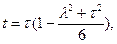
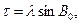
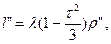(132)

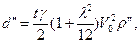
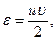
(133)

B₂ = B₀ - d", L₂ = L₁ + l", A_2,1 = A_1,2 + 180° + (t - ε)ρ". (134)

Пример 1.Заданы геодезические координаты пункта Q₁ (см. рис. 31):

широта В₁ = 60°, долгота L₁ = 10°, азимут А_1,2 = 45° геодезической линии Q₁Q₂ и её длина s = 60 000, 000 м.

Определить координаты пункта Q₂: широту В₂, долготу L₂; обратный азимут А_2,1.

Таблица 5

Решение прямой геодезической задачи по способу Шрейбера

B1	60°	γ	0,006 634 843
L1	10°	λ	0,013 424 515
A1	45°	τ	0,011 670 325
s	60 000,000 м	l"	46'08,8793"
V1	1,000 841 961	t	0,011 669 709
σ	0,009 391 235	d"	7,9985"
u	0,006 640 704	ε	0,000 022 049
υ	0,006 640 557	B2	60°22'42,8586"
B0	60°22'50,8587"	L2	10°46'08,8793"
V0	1,000 822 659	A2,1	225°40'02,50"

Решение обратной геодезической задачи на поверхности эллипсоида по формулам со средними аргументами

(способ К. Ф. Гаусса)

Исходные данные: B₁, L₁, B₂, L₂ (см. рис. 31 и 32).

Последовательность решения обратной геодезической задачи на малые расстояния (до 60 км)

1. Прежде всего, по заданным координатам B₁, L₁, B₂, L₂ находим:

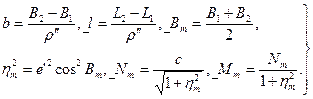
(135)

- 60 -

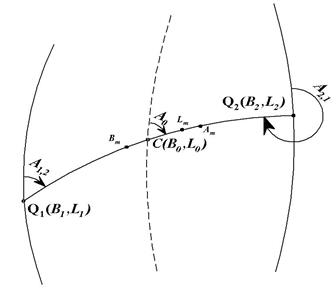
Рис. 32. Обратная геодезическая задача

(по формулам К. Ф. Гаусса)

2. С погрешностью на величину пятого порядка находим выражения:

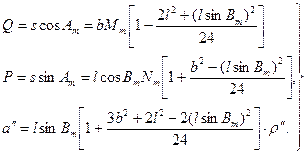(136)

3. 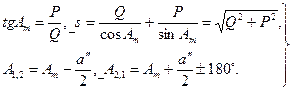Таким образом, решение задачи завершается применением следующих формул:

(137)

- 61 -

Пример 2.Заданы геодезические координаты пунктов Q₁ и Q₂ (см. рис. 31, 32): широты В₁ = 60°, В₂ = 60°22'42,8586", долготы L₁ = 10°, L₂ = 10°46'08,8792".

Определить: Прямой А_1,2 и обратный А_2,1 азимуты линии 1 - 2 и её длину S по формулам К. Ф. Гаусса.

Таблица 6

Решение обратной геодезической задачи по формулам К. Ф. Гаусса

Со средними аргументами

B1	60°	l ∙ sinBm	0, 11 647 553
B2	60°22'42,8586"	Q	42 178,607
L1	10°	P	42 672,768
L2	10°46'08,8792"	a"	2402,502"
b	0,006 607 325	Am	45°20'01,241"
l	0,013 423 905	A1,2	44°59'59,991"
Bm	60°11'21,4293"	A2,1	225°40'02,492"
Mm	6 383 745,14	S	60 000,000 м
Nm	6 394 376,55

Задание для студентов

По решению прямой и обратной геодезических задач

Каждый студент согласно варианту решает одну обратную и одну прямую геодезические задачи на поверхности эллипсоида Ф. Н. Красовского.

Номер варианта для решения обратной геодезической задачи соответствует номеру фамилии студента в списке группы (последняя цифра шифра в студенческой книжке - для студента заочной формы обучения). Исходные данные берутся из таблицы 7, согласно номеру варианта.

1. Студенты решают обратную геодезическую задачу.

2. На основе данных решения обратной геодезической задачи решают прямую геодезическую задачу - для контроля. В качестве исходных данных для решения прямой геодезической задачи принять:

- геодезические координаты пункта "Q₂ - Общий": B₂ = 53°22'18,91", L₂ = 58°59'17,87", значение длины стороны S и её азимут A_2,1;

- вычислить геодезические координаты B₁ и L₁ пункта Q₁, и прямой азимут A_1,2;

- результаты вычислений оформить в таблицах и сопроводить пояснениями по теории решения геодезических задач на поверхности эллипсоида вращения Ф. Н. Красовского.

- 62 -

Таблица 7

Варианты

для решения студентами обратной геодезической задачи