Вычисление длины дуги меридиана между двумя точками по формулам со средними аргументами
Контрольные вычисления
| Формулы | Результаты вычислений | Формулы | Результаты вычислений |
| a | 6 378 245,0 м | 0,25e2 sin2 Bср. | 0,000 909 66 |
| (1-e2) | 0,993 306 58 | 1,25e2sin2 Bср. | 0,004 548 32 |
| a(1-e2) | 6 335 552,717 | 1+0,25e2 sin2 Bср. | 1,000 909 66 |
| 1/6 ρ" | 8 080 228·10-13 | 1 - 1,25e2sin2 Bср. | 0,995 451 68 |
| B2 | 49°29'58,938" | 0,25e2 sin2 B'ср. | 0,000 938 67 |
| B1 | 45°30'17,221" | 1,25e2sin2 B'ср. | 0,004 693 36 |
| Bср. | 47°30' 08,079" | 1+0,25e2 sin2 B'ср. | 1,000 938 67 |
| B'ср. | 48°30' 03,508" | 1 - 1,25e2sin2 B'ср. | 0,995 306 64 |
| B"ср. | 46°30' 12,650" | 0,25e2 sin2 B"ср. | 0,000 880 57 |
| e2 | 0,006 693 42 | 1,25e2sin2 B"ср. | 0,004 402 84 |
| 0,25e2 | 0,001 673 36 | 1+0,25e2 sin2 B"ср. | 1,000 880 57 |
| 1,25e2 | 0,008 366 77 | 1 - 1,25e2sin2 B"ср. | 0,995 597 16 |
| sinBср. | 0,737 303 80 | Mср. | 6 370 290,021 |
| sinB'ср. | 0,748 966 99 | M'ср. | 6 371 402,932 |
| sinB"ср. | 0,725 416 58 | M"ср. | 6 369 174,032 |
| sin2 Bср | 0,543 616 89 | (B2 - Bср.)" | 7 190,859" |
| sin2 B'ср | 0,560 951 55 | (B2 - Bср.)"/6 ρ" | 0,005 810 378 |
| sin2 B"ср | 0,526 229 21 | (Mср. + 4М"ср. +М1) | 38 215 042,473 |
| (Bср. - B1)" | 7190,858 | X2 | 222 121,530 |
| (Bср. - B1)" /6 ρ" | 0,005 810 377 | X1 | 222 043,811 |
| M1 | 6 368 056,324 | X2 + X1 = S м | 444 165,341 м |
| M2 | 6 372 511,409 | ||
| (M2 + 4M'ср.+Мср.) | 3 822 8413,158 |
Пример 2. Вычисление длины дуги параллели между двумя точками, лежащими на этой параллели, если даны разность долгот точек l = L2 - L1 = 0°45'46,882" и широта параллели B = 54°32'19,354".
Схема решения
| Формулы | Результаты вычислений | Формулы | Результаты вычислений |
| l | 0°45'46,882" | 1-0,25e2 sin2 B | 0,99888986 |
| B | 54°32'19,354" | 1-0,75e2 sin2 B | 0,99666958 |
| a | 6 378 245 м | N | 6 392 453,854 м |
| 0,25e2 | 0,00167336 | cos B | 0,58015280 |
| 0,75e2 | 0,00502006 | l" | 2 746,882" |
| sin B | 0,81450766 | 1/ρ" | 4 848 137∙10-12 |
| sin2 B | 0,66342273 | N cos B | 3 708 600,002 |
| 0,25e2 sin2 B | 0,00111014 | l"/ρ" | 0,01331726 |
| 0,75e2 sin2 B | 0,00333042 | SП | 49 388,390 м |
- 37 -
Контрольные вычисления
| Формулы | Результаты вычислений | Формулы | Результаты вычислений |
| N cos B | 3 708 600,002 | Y1 | 32 363,641 |
| 1/ρ" | 4 848 137∙10-12 | Y2 | 81 752,029 |
| (l"+1800")/ρ" | 0,0220439060 | SП=Y2-Y1 | 49 388,388 м |
| 1800"/ρ" | 0,0087266466 |
Вычисление длин сторон и площади съёмочной трапеции
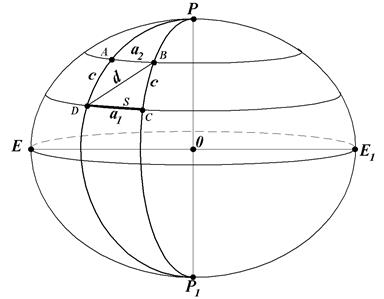 |
Рис. 22. Съёмочная трапеция
Съёмочная трапеция, строго говоря, представляет собой часть поверхности эллипсоида, ограниченную меридианами и параллелями
(рис. 22). Поэтому стороны трапеции равны длинам дуг меридианов и параллелей, вычисляемых по формулам (79) и (91). Северная и южная стороны рамки являются дугами параллелей a1 и а2, а восточная и западная - дугами меридианов с, равными между собой. Диагональ трапеции d.
- 38 -
Рабочие формулы:
(размеры в сантиметрах)
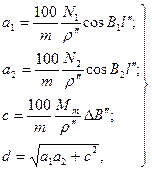 |
(98)
где m - знаменатель масштаба съёмки; l = LC - LD - разность долгот точек C и D; N1, N2 - радиусы кривизны первого вертикала в точках с широтами B1 и B2; Mm - радиус кривизны меридиана в точке с широтой
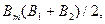 | 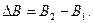 | ||
Стороны трапеции в формулах (98) получаются в сантиметрах.
Практически съёмка масштабов 1 : 1000 000 - 1 : 25 000 выполняется с использованием 6- градусной зоны, съёмка более крупного масштаба - с использованием 3 - градусной зоны. В указанных случаях искажения длин сторон рамок съёмочных трапеций в проекции Гаусса - Крюгера ничтожно малы и ими пренебрегают.
Пример 1. Рассчитать размеры трапеции масштаба 1:50000, ограниченной параллелями с широтами В1 = 50°00' и B2 = 50°10'. Интервал трапеции указанного масштаба по долготе будет l = 15' = 900". Величина ∆B = B2 - B1 = 10' = 600".
В таблице радиусы кривизны меридиана M и первого вертикала N вычисляются по формулам:
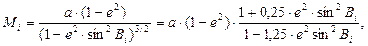 | |||
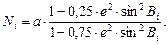 |
- 39 -
Схема решения
| Формулы | Результаты вычислений | Формулы | Результаты вычислений |
| a | 6 378 245 | 1-0,25e2sin2B1 | 0,99902 |
| a(1-e2) | 6 335 552 | 1-0,75e2sin2B1 | 0,99705 |
| e2 | 0,00669342 | 1-0,25e2sin2B2 | 0,99901 |
| 0,25e2 | 0,0016734 | 1-0,75e2sin2B2 | 0,99704 |
| 0,75e2 | 0,0050201 | 1+0,25e2sin2Bm | 1,00098 |
| 1,25e2 | 0,0083668 | 1-0,25e2sin2Bm | 0,99508 |
| B1 | 50°00'00" | N1 | 6 390 847 |
| B2 | 50°10'00" | N2 | 6 390 847 |
| Bm | 50°05'00" | Mm | 6 373 116 |
| sin B1 | 0,76604 | 1/ ρ" | 4 848 137∙10-12 |
| sin B2 | 0,76791 | N1 /ρ" | 30,984 |
| sin Bm | 0,76698 | N2 /ρ" | 30,984 |
| sin2 B1 | 0,58682 | Mm / ρ" | 30,898 |
| sin2 B2 | 0,58969 | a1 | 35,849 |
| sin2 Bm | 0,58826 | a2 | 35,725 |
| cos B1 | 0,64279 | c | 37,078 |
| cos B2 | 0,64056 | a1 a2 | 1280,70 |
| 100l/m | 9/5 = 1,8 | d2 | 2655,48 |
| 100∆B/m | 6/5 = 1,2 | d | 51,531 |
Пример 2. Вычисление на поверхности эллипсоида Красовского площади трапеции масштаба 1 : 100 000, ограниченной параллелями с широтами В1 = 50°00' и B2 = 50°20' с точностью до 0,001 км2. Разность долгот меридианов, ограничивающих лист карты этого масштаба равен
l = ∆L = L2 - L1 = 30' = 1800".
Основные формулы:
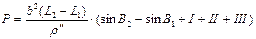 |
, (99)
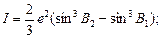 |
где
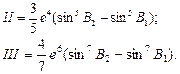 |
- 40 -
Схема решения
| Формулы | Результаты вычислений | Формулы | Результаты вычислений |
| b | 6 356,863 м | sin7 B1 | 0,15480242 |
| e2 | 0,00669342 | (2/3) e2 | 0,00446228 |
| 1/ ρ" | 4 848 137∙10-12 | (3/5) e4 | 0,00002688 |
| L2 - L1 | 1800" | (4/7) e6 | 0,00000017 |
| sin B2 | 0,76977104 | I | 0,00002942 |
| sin3 B2 | 0,45612587 | II | 0,00000017 |
| sin5 B2 | 0,27027622 | III | 0,00000000 |
| sin7 B2 | 0,16015148 | b2(L2 -L1)"/ ρ" | 352 641,9 км2 |
| sin B1 | 0,76604444 | b2 | 40 409 707,2 км2 |
| sin3 B1 | 0,44953332 | sinB2 -siB1+I+II+III | 0,00375619 |
| sin5 B1 | 0,26379698 | P | 1324,590 км2 |
