Кафедра Маркшейдерского дела, геологии и

Кафедра Маркшейдерского дела, геологии и

Обогащения полезных ископаемых

ВЫСШАЯ ГЕОДЕЗИЯ

Практикум

Часть I

Учебно - методическое пособие

по дисциплине "Высшая геодезия"

для студентов очной и заочной форм обучения

специализации 130402 - "Маркшейдерское дело",

специальности 130400 - "Горное дело"

Магнитогорск

Составитель В.Н. Хонякин

Высшая геодезия. Практикум. Часть I. Учебно-методическое пособие по дисциплине "Высшая геодезия" для студентов очной и заочной форм обучения специализации 130402 - "Маркшейдерское дело", специальности 130402 - "Горное дело",. Магнитогорск: МГТУ, 2015.

В учебно-методическом пособии рассмотрены вопросы, имеющие большое практико-теоретическое значение в деятельности маркшейдера. Пособие содержит 8 разделов: введение; форма и размеры Земли; основные системы координат, применяемые в геодезии; главные радиусы кривизны поверхности эллипсоида в данной точке; кривые на поверхности эллипсоида вращения; решение сфероидических (сферических) треугольников; вычисление геодезических широт, долгот и азимутов; система плоских прямоугольных координат в проекции Гаусса-Крюгера.

В разделе "Введение" даны сведения об основе предмета и основных понятиях высшей геодезии.

В разделе "Форма и размеры Земли" изложены сведения о уровенных поверхностях, геоиде, земном эллипсоиде.

В разделе "Основные системы координат, применяемых в геодезии" представлены системы координат, определяющих положение точек поверхности Земли и связь систем координат.

В разделе "Главные радиусы кривизны поверхности эллипсоида в данной точке" рассматриваются главные радиусы нормальных сечений поверхности эллипсоида, вычисление длин дуг меридианов и параллелей, вычисление длин сторон и площадей съёмочных трапеций, даётся понятие геодезической линии.

В разделах "Решение сфероидических (сферических) треугольников"; "Вычисление геодезических широт, долгот и азимутов" изложены способы решения главных геодезических задач на поверхности эллипсоида вращения.

В разделе "Система плоских прямоугольных координат в проекции Гаусса-Крюгера" излагается принцип проектирования точек поверхности Земли на горизонтальную плоскость и методы решения различных задач в данной проекции.

В пособии приведены примеры решения задач Высшей геодезии по всем разделам, что способствует закреплению знаний теоретического материала и даёт практический навык их решения.

Хонякин В.Н., 2015.

I. Введение

§ 1. Предмет и основные понятия высшей геодезии.

Высшая геодезия - наука, предметами изучения которой являются Земля и другие планеты солнечной системы: их форма, размеры и гравитационные поля. Задачи высшей геодезии делятся на научные и научно-технические (практические).

Главная научная задача состоит в изучении фигуры Земли. В настоящее время под фигурой Земли понимают физическое тело, ограниченное физической поверхностью Земли, т. е. поверхностью её твёрдой оболочки на суше и невозмущённой поверхностью вод морей и океанов. Задача изучения фигуры Земли разделяется на две части:

1) установление формы, размеров и положения в теле Земли некоторой достаточно простой геометрической фигуры - "фигуры относимости"; обычно в качестве такой фигуры принимают эллипсоид вращения;

2) определение отступлений поверхности действительной фигуры Земли от поверхности принятого эллипсоида. Обе задачи решают на основании результатов астрономических, геодезических и гравиметрических измерений.

Высшая геодезия располагает эффективными методами и средствами точных измерений и научной математической обработки их результатов, благодаря которым имеется возможность изучения таких проблем, как:

а) исследование структуры земной коры;

б) исследование деформаций земной коры (горизонтальных и вертикальных, периодических и непериодических);

в) определение уровней вод морей и океанов;

г) изучение движения земных полюсов и других явлений, обусловливаемых жизнью Земли в целом.

Важнейшей научно-технической задачей является научно обоснованное решение программных и методических вопросов построения и математической обработки государственных геодезических сетей. Эти сети необходимы для картографирования территории страны, для решения задач инженерной геодезии и для обороны страны.

Соответственно постановке этих задач в высшей геодезии изучаются программы и методы построения геодезических сетей: триангуляции, полигонометрии, трилатерации, комбинированных и нивелирных сетей, а также космических, создаваемых с использованием искусственных спутников Земли.

- 3 -

Изучаются технические средства (приборы и инструменты) для выполнения высокоточных геодезических измерений, а также методы математической обработки результатов измерений, выполняемых при развитии этих сетей.

II. Форма и размеры Земли

Рис. 1. К понятию о силе Рис. 2. Направления силы

тяжести Земли тяжести Земли

Геодезические измерения, выполняемые в любой точке физической поверхности Земли, связаны с направлением отвесной линии в этой точке. Например, при измерении горизонтального угла теодолитом, ось вращения его совмещают с отвесной линией, проходящей через вершину угла. Геометрическое нивелирование выполняют горизонтальным лучом визирования, т.е. перпендикулярным отвесной линии в точке установки нивелира. Измеренное расстояние между точками местности проектируют на горизонтальную плоскость при помощи отвесных линий в этих точках.

Простейший прибор - отвеспоказывает направление действия силы тяжести Земли; подвешенный на нити груз под действием силы тяжести натягивает нить, которая и указывает направление отвесной линии в данной точке.

- 4 -

Из курса физики известно, что сила тяжести G есть равнодействующая двух сил: силы притяжения ЗемлиF и центробежной силы P (рис. 1). Вектор силы F направлен приблизительно к центру Земли. Наибольшее значение силаF имеет на полюсах и наименьшее - на экваторе. Сила Pимеет максимальное значение на экваторе, где она составляет приблизительно 1:288 от величины F. На полюсах сила P равна нулю. Следовательно, сила G на земной поверхности непрерывно увеличивается от экватора к полюсам и на полюсах имеет максимальное значение. В свою очередь сила земного притяженияF есть равнодействующая притяжений всех масс, заключенных в теле Земли. Значит, величина и направление силы обусловлены распределением этих масс. Отсюда следует, что и направление отвесной линии тоже зависит от распределения масс в теле Земли.

Из курса физики известно, что в гравитационном поле Земли работа силы тяжести не зависит от формы пути MN (рис. 3), а зависит только от положения начальной и конечной точек этого пути. Поле, обладающее таким свойством, называется потенциальным. Во всяком потенциальном поле можно провести так называемые уровенныеповерхности, т.е. такие поверхности, при движении материальной точки по которым сила поля работы не совершает. Нетрудно доказать, что в гравитационном поле Земли расстояние между уровенными поверхностями убывает к полюсам.

Рис. 3. К понятию о Рис. 4. Не параллельность

работе силы тяжести уровенных поверхностей

Согласно сказанному выше о работе силы тяжести, можем написать выражения для работы по пути MaNи по пути MbN и приравнять их:

где ∆h₁ и ∆h₂ - расстояния между уровенными поверхностями.

- 5 -

Возьмём две точки M и N в плоскости земного меридиана, лежащие на разных, но близких одна к другой, уровенных поверхностях (рис. 4).

g₁ и g₂ - величины ускорений силы тяжести в точкахM и N. Сила тяжести G возрастает к полюсам, следовательно, g₂ >g₁ . Поэтому из равенства легко увидеть, что Δh₂< Δh₁ . Вывод: уровенные поверхности гравитационного поля Земли между собой непараллельны и расстояние между ними уменьшается к полюсам.

Рис. 5. Уровенные поверхности Рис. 6. Направление

и силовые линии гравитационного отвесной линии

поля Земли

Линии, нормальные к уровенным поверхностям, называются силовыми линиями (см. рис. 5). Касательная к силовой линии в данной точке есть отвесная линия в этой точке. Следовательно, отвесная линия является нормалью к уровенной поверхности (рис. 6). Поверхность воды в спокойном состоянии является одной из уровенных поверхностей. Можно провести бесчисленное множество уровенных поверхностей; каждая из них вблизи земной поверхности будет поверхностью неразрывной, замкнутой, без складок и рёбер. Вид уровенной поверхности зависит от распределения масс в теле Земли.

При равномерном распределении масс (см. рис. 7) эта поверхность будет занимать положение, показанное пунктиром.

При наличии массы M с преувеличенной плотностью уровенная поверхность будет иметь некоторый изгиб кверху.

- 6 -

.

Рис. 7. Вид уровенной поверхности

В данной точке

Радиус кривизны геодезического меридиана в данной точке равен

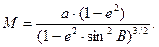(55)

Из (55) ясно, что М возрастает при изменении широты В от 0 до 90°.

- 26 -

Радиус кривизны меридианного эллипса в полюсах (при В = 90°) обозначим через с, тогда

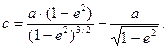(56)

Принимая во внимание, что

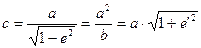
(57)

и обозначив

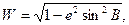(58)

напишем

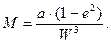(59)

Введём ещё функцию

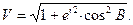(60)

Так как, согласно (13) и (14)

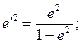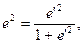то

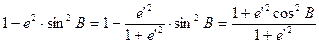
и

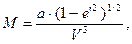(61)

- 27 -

или, согласно (57),

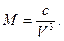(62)

W и V - соответственно называются первой и второй основными функциями геодезической широты В.

Заменяя в (55) первый эксцентриситет его выражением через полуоси эллипсоида и используя обозначения (52), формула (55) для М перепишется

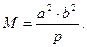
(63)

Для определения радиуса N первого вертикала заметим, что если сечение первого вертикала VMW (рис. 18) - нормальное, то параллель MQS - наклонное сечение, поскольку нормаль не лежит в плоскости этого сечения. Указанные два сечения в точке М имеют общую касательную. Для доказательства этого положения проведём в точке М касательную к параллели МТ; эта касательная, лежащая в плоскости MQSC, перпендикулярной к меридианной плоскости ME₁P₁, перпендикулярна к прямой МС, образованной пересечением этих плоскостей. Таким образом, касательная МТ перпендикулярна к плоскости меридиана РМЕ₁Р₁, поэтому плоскость первого вертикала будет содержать прямую МТ; если Mn - нормаль к поверхности эллипсоида в точке М, то угол TMn равен 90°, следовательно, МТ будет касательной и к кривой EMW.

Имея это в виду, воспользуемся теоремой: если через точку поверхности проведены два сечения - нормальное и наклонное, причём в рассматриваемой точке эти два сечения имеют общую касательную, то радиус кривизны наклонного сечения равен радиусу кривизны нормального сечения, умноженному на косинус угла между плоскостями этих двух сечений.

Из рис. 18 следует, что угол между плоскостями параллели и первого вертикала измеряется углом CMn = B. Поэтому радиус r параллели определится через радиус кривизны первого вертикала N по формуле

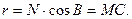(64)

Учитывая выражение (26) для радиуса параллели, получаем

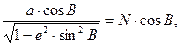(65)

- 28 -

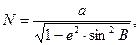откуда (66)

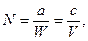или (67)

принимая во внимание обозначение (52), получим

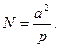(68)

Из рис. 18 следует, что

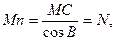(69)

т. е. длина отрезка нормали Mn равна радиусу кривизны первого вертикала.

Радиус кривизны меридиана М служит для вычисления длин дуг меридианов и разностей широт; радиус кривизны первого вертикала N -для вычисления длин дуг параллелей и разностей долгот и азимутов.

Значения радиусов кривизны М и N с ошибкой не более 0,00005 м вычисляются по формулам:

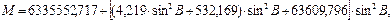(70)

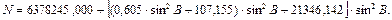(71)

С ошибкой менее 0,2 м главные радиусы кривизны эллипсоида вычисляются по формулам:

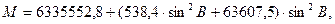(72)

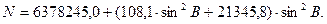(73)

Примеры

Схема решения

Формулы	Результаты вычислений	Формулы	Результаты вычислений
a e2	6 378 245,0 м 0,006 693 42	a e2	6 378 245,0 м 0,006 693 42
a(1-e2)	633 5552,717 м	1,25e2sin2 B1	0,004 257 10
1/6 ρ"	8 080 228·10-13	1,25e2sin2 B2	0,004 837 77
B2	49°29'58,938"	1,25e2sin2 Bср.	0,004 548 32
B1	45°30'17,221"	1+0,25e2 sin2 B1	1,000 851 42
Bср.	47 30 08,080	1+0,25e2 sin2 B2	1,000 967 56
0,25e2	0,001 673 36	1+0,25e2 sin2 Bср.	1,000 909 66
1,25e2	0,008 366 78	1 - 1,25e2 sin2 B1	0,995 742 90
sinB1	0,713 308 97	1 - 1,25e2 sin2 B2	0,995 162 23
sinB2	0,760 402 63	1 - 1,25e2sin2 Bср.	0,995 451 68
sinBср.	0,737 303 80	M1	6 368 056,324 м
sin2 B1	0,508 809 69	M2	6 372 511,409 м
sin2 B2	0,578 212 16	Mср.	6 370 290,021 м
sin2 Bср.	0,543 616 89	(B2 - B1)"	14 381,717"
0,25e2 sin2 B1	0,000 851 42	(B2 - B1)"/6 ρ"	0,011 620 755
0,25e2 sin2 B2	0,000 967 56	S, м	444 165,343 м
0,25e2 sin2 Bср.	0,000 909 66

- 36 -

Таблица 2

Контрольные вычисления

Формулы	Результаты вычислений	Формулы	Результаты вычислений
a	6 378 245,0 м	0,25e2 sin2 Bср.	0,000 909 66
(1-e2)	0,993 306 58	1,25e2sin2 Bср.	0,004 548 32
a(1-e2)	6 335 552,717	1+0,25e2 sin2 Bср.	1,000 909 66
1/6 ρ"	8 080 228·10-13	1 - 1,25e2sin2 Bср.	0,995 451 68
B2	49°29'58,938"	0,25e2 sin2 B'ср.	0,000 938 67
B1	45°30'17,221"	1,25e2sin2 B'ср.	0,004 693 36
Bср.	47°30' 08,079"	1+0,25e2 sin2 B'ср.	1,000 938 67
B'ср.	48°30' 03,508"	1 - 1,25e2sin2 B'ср.	0,995 306 64
B"ср.	46°30' 12,650"	0,25e2 sin2 B"ср.	0,000 880 57
e2	0,006 693 42	1,25e2sin2 B"ср.	0,004 402 84
0,25e2	0,001 673 36	1+0,25e2 sin2 B"ср.	1,000 880 57
1,25e2	0,008 366 77	1 - 1,25e2sin2 B"ср.	0,995 597 16
sinBср.	0,737 303 80	Mср.	6 370 290,021
sinB'ср.	0,748 966 99	M'ср.	6 371 402,932
sinB"ср.	0,725 416 58	M"ср.	6 369 174,032
sin2 Bср	0,543 616 89	(B2 - Bср.)"	7 190,859"
sin2 B'ср	0,560 951 55	(B2 - Bср.)"/6 ρ"	0,005 810 378
sin2 B"ср	0,526 229 21	(Mср. + 4М"ср. +М1)	38 215 042,473
(Bср. - B1)"	7190,858	X2	222 121,530
(Bср. - B1)" /6 ρ"	0,005 810 377	X1	222 043,811
M1	6 368 056,324	X2 + X1 = S м	444 165,341 м
M2	6 372 511,409
(M2 + 4M'ср.+Мср.)	3 822 8413,158

Пример 2. Вычисление длины дуги параллели между двумя точками, лежащими на этой параллели, если даны разность долгот точек l = L₂ - L₁ = 0°45'46,882" и широта параллели B = 54°32'19,354".

Схема решения

Формулы	Результаты вычислений	Формулы	Результаты вычислений
l	0°45'46,882"	1-0,25e2 sin2 B	0,99888986
B	54°32'19,354"	1-0,75e2 sin2 B	0,99666958
a	6 378 245 м	N	6 392 453,854 м
0,25e2	0,00167336	cos B	0,58015280
0,75e2	0,00502006	l"	2 746,882"
sin B	0,81450766	1/ρ"	4 848 137∙10-12
sin2 B	0,66342273	N cos B	3 708 600,002
0,25e2 sin2 B	0,00111014	l"/ρ"	0,01331726
0,75e2 sin2 B	0,00333042	SП	49 388,390 м

- 37 -

Контрольные вычисления

Формулы	Результаты вычислений	Формулы	Результаты вычислений
N cos B	3 708 600,002	Y1	32 363,641
1/ρ"	4 848 137∙10-12	Y2	81 752,029
(l"+1800")/ρ"	0,0220439060	SП=Y2-Y1	49 388,388 м
1800"/ρ"	0,0087266466

Схема решения

Формулы	Результаты вычислений	Формулы	Результаты вычислений
a	6 378 245	1-0,25e2sin2B1	0,99902
a(1-e2)	6 335 552	1-0,75e2sin2B1	0,99705
e2	0,00669342	1-0,25e2sin2B2	0,99901
0,25e2	0,0016734	1-0,75e2sin2B2	0,99704
0,75e2	0,0050201	1+0,25e2sin2Bm	1,00098
1,25e2	0,0083668	1-0,25e2sin2Bm	0,99508
B1	50°00'00"	N1	6 390 847
B2	50°10'00"	N2	6 390 847
Bm	50°05'00"	Mm	6 373 116
sin B1	0,76604	1/ ρ"	4 848 137∙10-12
sin B2	0,76791	N1 /ρ"	30,984
sin Bm	0,76698	N2 /ρ"	30,984
sin2 B1	0,58682	Mm / ρ"	30,898
sin2 B2	0,58969	a1	35,849
sin2 Bm	0,58826	a2	35,725
cos B1	0,64279	c	37,078
cos B2	0,64056	a1 a2	1280,70
100l/m	9/5 = 1,8	d2	2655,48
100∆B/m	6/5 = 1,2	d	51,531

Пример 2. Вычисление на поверхности эллипсоида Красовского площади трапеции масштаба 1 : 100 000, ограниченной параллелями с широтами В₁ = 50°00' и B₂ = 50°20' с точностью до 0,001 км². Разность долгот меридианов, ограничивающих лист карты этого масштаба равен

l = ∆L = L₂ - L₁ = 30' = 1800".

Основные формулы:

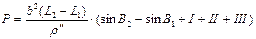, (99)

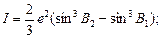где

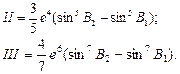- 40 -

Схема решения

Формулы	Результаты вычислений	Формулы	Результаты вычислений
b	6 356,863 м	sin7 B1	0,15480242
e2	0,00669342	(2/3) e2	0,00446228
1/ ρ"	4 848 137∙10-12	(3/5) e4	0,00002688
L2 - L1	1800"	(4/7) e6	0,00000017
sin B2	0,76977104	I	0,00002942
sin3 B2	0,45612587	II	0,00000017
sin5 B2	0,27027622	III	0,00000000
sin7 B2	0,16015148	b2(L2 -L1)"/ ρ"	352 641,9 км2
sin B1	0,76604444	b2	40 409 707,2 км2
sin3 B1	0,44953332	sinB2 -siB1+I+II+III	0,00375619
sin5 B1	0,26379698	P	1324,590 км2

Взаимные нормальные сечения

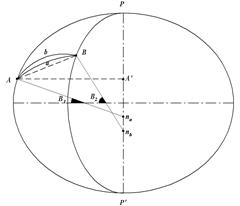Рис. 24. Нормальные сечения

В точках А и В поверхности эллипсоида (рис. 24) с широтами В₁ и В₂ (В₂>В₁) проведём нормали n_a и n_b к поверхности до их пересечения с осью вращения PP'. Нормальные плоскости AaBn_a и AbBn_b образуют с поверхностью эллипсоида кривые АaВ и ВbА, которые называются взаимно обратными нормальными сечениями.

Видно, что несовпадение прямых и обратных нормальных сечений

- 41 -

приводит к тому, что измеренные горизонтальные углы на трёх пунктах треугольника не образуют на поверхности эллипсоида замкнутого треугольника; фигура получается "разорванной". Эту неопределённость в образовании треугольников можно устранить, если вершины соединять геодезическими линиями.

Геодезическая линия

Между двумя точками на любой поверхности можно провести множество кривых.

В геодезии решение задач по определению взаимного положения точек земной поверхности основано на построении на ней определённых фигур (обычно треугольников) и вычислении числовых значений элементов этих фигур. Поэтому следует решить, какими кривыми соединять точки поверхности земного эллипсоида при вычислении элементов геодезических построений.

В сфероидической геодезии точки на поверхности эллипсоида соединяются г е о д е з и ч е с к и м и л и н и я м и, которые определяются как кратчайшие расстояния между ними.

Геодезическая линия на поверхности - такая кривая, в каждой точке которой соприкасающаяся плоскость проходит через нормаль к поверхности в той же точке. Если на поверхности эллипсоида взять три близкие точки M, N, K, через которые провести плоскость,то предельное положение плоскости при M → N и K → N носит название с о п р и -

к а с а ю щ е й с я п л о с к о с т и; касательная в точке N лежит в соприкасающейся плоскости; главная нормаль в точке N совпадает с нормалью к поверхности.

Из определения геодезической линии и понятия соприкасающейся плоскости можно представить следующий геометрический метод построения геодезической линии на поверхности земного эллипсоида.

Пусть РР₁ (рис. 26) - малая ось эллипсоида, An₁ - нормаль к поверхности эллипсоида в точке А. Установим в точке А теодолит так, чтобы его ось вращения совпала с нормалью к поверхности эллипсоида в данной точке.

После этого в заданном направлении отметим на поверхности эллипсоида точку а, близкую к точке А. Перенесём теодолит в точку а, совместим ось вращения его с нормалью an₂ к поверхности эллипсоида, наведём трубу на точку А, повернём алидаду горизонтального круга точно на 180° и отметим на поверхности эллипсоида к а точку b. Затем перенесём теодолит в точку b, установим его ось вращения по нормали bn₃, наведём трубу на точку а, повернём алидаду точно на 180° и в коллимационной плоскости наметим точку с, близкую к точке b.

- 44 -

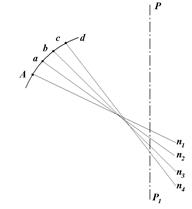- 44 -

Рис. 26. Пример построения геодезической линии

Поступая таким образом до тех пор, пока расстояние между начальной точкой А и соответствующей точкой i не сделается равным заданному, и предполагая, что указанные выше перестановки теодолита производились через бесконечно малые расстояния, получаем на поверхности эллипсоида

г е о д е з и ч е с к у ю линию (рис. 27).

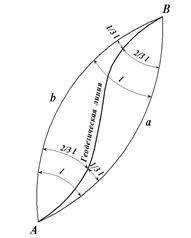Рис. 27. Вид геодезической линии:

AaB - прямое нормальное сечение в точке А; AbB - обратное нормальное сечение в точке А; BbA - прямое нормальное сечение в точке В; BaA - обратное нормальное сечение в точке В.

- 45 -

Геодезическая линия на поверхности эллипсоида (при азимутах, не близких к 90 или 270°) делит угол между взаимными нормальными сечениями в отношении 1:2 и располагается в данной точке ближе к прямому нормальному сечению.

Другими словами, угол между геодезической линией, соединяющей точки

А и В, и прямым нормальным сечением в каждой из этих точек равен 1/3 угла между прямым и обратным нормальными сечениями в данной точке. Эта зависимость используется для получения формулы поправки в направления за переход от прямого нормального сечения к геодезической линии.

Общие сведения

Редукционная проблема - совокупность задач по переходу от непосредственно измеренных величин на поверхности Земли к соответствующим им величинам на поверхности фигуры относимости - на поверхности эллипсоида вращения.

- 49 -

Треугольник, образованный геодезическими линиями на поверхности эллипсоида (сфероида), называется сфероидическим треугольником.

Решить треугольник - это значит определить все его элементы (стороны, углы), в то время как некоторые из них должны быть известны.

Сфероидический треугольник нельзя решить, используя элементарные функции. Сторона сфероидического треугольника, например, в триангуляции 1 класса, имеет длину от 20 до 60 км. В навигации, космической геодезии, при связи геодезических сетей разных стран и континентов стороны треугольников могут достигать сотен километров.

Теоретические расчёты показывают, что, если необходимо решить треугольник с относительной ошибкой в длинах его сторон 10^-8, то сфероидический треугольник можно рассматривать как сферический, если его стороны не превышают 240 км. Сумма внутренних углов сферического треугольника (А + В + С) равна 180° + ε, где ε - сферический избыток.

В связи с этим в геодезической практике применяют специальные методы решения этих треугольников: по теореме Лежандра и способу аддитаментов.

1. Решение сферического треугольника по теореме Лежандра

Рис. 30. Теорема Лежандра

Способ сферических избытков, предложенный А. Лежандром в 1787 г. (теорема Лежандра), состоит в следующем: каждый из углов сферического треугольника А, В и С уменьшают на одну треть сферического избытка ε. В результате этого получают углы плоского треугольника А₁, В₁ и С₁ и,

- 50 -

оставляя стороны a, b, c сферического треугольника без изменений, решают его как плоский по теореме синусов (рис. 30). Другими словами, от исходного сферического треугольника переходят к соответствующему плоскому треугольнику с теми же сторонами, но с исправленными углами.

Рабочие формулы

; ; ; (115)

(116)

(117)

(118)

- средний радиус кривизны эллипсоида для средней

широты B_m.

(119)

Пример 1.Решение сферического треугольника АВС звена триангуляции 1 класса, если даны измеренные, приведённые к центрам знаков и спроецированные на поверхность эллипсоида его углы

А = 50°20'19,41'', В = 62°12'44,54'', С = 67°26'58,43'' и

сторона b = 44 797,282 м. Средняя широта треугольника B_m =48°12'

(см. рис. 30).

Решение треугольника

Вершина	Измеренные углы сфери-ческого тре-угольника	По-прав-ки в углы - ω /3	Уравненные углы сфери- ческого треуголь- Ника	- ε/3	Углы плоского треугольника	Синусы уг- лов плоско- го треуголь- ника
В	69°12'44,54"	+0,57	69°12'45,11"	-1.36	69°12'43,75"	0,88467988
А	50 20 19,41	+0,57	50 20 19,98	-1.36	50 20 18,62	0,76982866
С	67 26 58,43	+0,57	67 26 59,00	-1.37	67 26 57,63	0,92354082
Σ	180°00'02,38"		180°00'04,09"		180°00'00,00"
ε	04,09
ω	-01,71

ω = Σ - (ε + 180°) - угловая невязка треугольника.

B 44 797.282 м c 46 765.073 м

- 52 -

По способу аддитаментов

В основе способа аддитаментов, предложенного И. Зольднером в 1820 г., лежит теорема синусов (см. рис. 30)

. (120)

Ввиду малости величин a/R, b/R, c/R, выражающих стороны сферического треугольника в радианной мере, по сравнению с радиусом Земли R, синусы этих величин можно разложить в ряд.

Ограничиваясь двумя первыми членами разложения, получим

. (121)

Идея способа аддитаментов заключается в том, что стороны сферического треугольника a, b, c исправляют поправками, в результате чего получают стороны плоского треугольника a' ,b', c' и неизвестные стороны сферического треугольника.

При этом, в логарифмическом варианте, аддитаментами называют поправки в логарифмы сторонA_a, A_b, A_c. В случае нелогарифмического решения, как видно из (121), аддитаментами являются величины

(122)

где - средний радиус кривизны эллипсоида для

района расположения треугольника.

П р и м е ч а н и е. Значение величин