Передача параметров в функции по значению и по ссылке

Список параметров, передаваемый в функции, состоит из имен параметров и указаний на их тип. Например, в заголовке:

double FSum(double x1, double x2, int a)

указано три параметра X1, Х2, A и определены их типы. Вызов такой процедуры может иметь вид:

Pr(Y, Х2, 5);

Это только один из способов передачи параметров в процедуру, называемый передачей по значению. Работает он так. В момент вызова функции в памяти соз­даются временные переменные с именами X1, Х2, А, и в них копируются значе­ния аргументов Y, Х2 и константы 5. На этом связь между аргументами и пере­менными X1, Х2, А разрывается. Вы можете изменять внутри процедуры значе­ния X1, Х2 и А, но это никак не отразится на значениях аргументов. Аргументы при этом надежно защищены от непреднамеренного изменения своих значений вызванной функцией. Это предотвращает случайные побочные эффекты, которые так сильно мешают иногда созданию корректного и надежного программного обес­печения.

К недостаткам такой передачи параметров по значению относятся затраты времени на копирование значений и затраты памяти для хранения копии. Если речь идет о какой-то переменной простого типа, это, конечно, не существенно. Но если, например, аргумент — массив из тысяч элементов, то соображения затрат времени и памяти могут стать существенными.

Еще одним недостатком передачи параметров по значению является невоз­можность из функций изменять значения некоторых аргументов, что во многих случаях очень желательно.

Возможен и другой способ передачи параметров — вызов по ссылке. В случае вызова по ссылке оператор вызова дает вызываемой функции возможность прямо­го доступа к передаваемым данным, а также возможность изменения этих данных. Вызов по ссылке хорош в смысле производительности, потому что он исключает накладные расходы на копирование больших объемов данных; в то же время он может ослабить защищенность, потому что вызываемая функция может испортить передаваемые в нее данные.

Вызов по ссылке можно осуществить двумя способами: с помощью ссылочных параметров и с помощью указателей. Ссылочный параметр — это псевдоним соот­ветствующего аргумента. Чтобы показать, что параметр функции передан по ссыл­ке, после типа параметра в прототипе функции ставится символ амперсанда (&); такое же обозначение используется в списке типов параметров в заголовке функ­ции. Перед амперсандом и после него могут вставляться пробельные символы. Например, идентичные объявления:

int &count

int & count

int& count

в списке параметров заголовка функции могут читаться как «count является ссыл­кой на int». В вызове такой функции достаточно указать имя переменной и она бу­дет передана по ссылке. Реально в функцию передается не сама переменная, а ее адрес, полученный операцией адресации (&). Тогда упоминание в теле вызываемой функции переменной по имени ее параметра в действительности является обраще­нием к исходной переменной в вызывающей функции и эта исходная переменная может быть изменена непосредственно вызываемой функцией.

Например:

void square(int &); // Прототип функции вычисления квадрата

void square(int &a) // Заголовок функции

{

a *= a; // Изменение значения параметра

}

Вызываться подобная функция может обычным способом передачей в нее име­ни аргумента. Например:

int х1 = 2;

square(xl);

В результате подобного вызова переменная xl получит значение 4.

Поскольку ссылочные параметры упоминаются в теле вызываемой функции просто по имени, программист может нечаянно принять ссылочный параметр за параметр, переданный по значению. Это может привести к неприятным ошибкам, если исходные значения переменных изменяются вызывающей функцией.

Альтернативной формой передачи параметра по ссылке является использова­ние указателей. Тогда адрес переменной передается в функ­цию не операцией адресации (&), а операцией косвенной адресации (*). В списке параметров подобной функции перед именем переменной указывается символ, свидетельствуя о том, что передается не сама переменная, а указатель на нее. В теле функции тоже перед именем параметра ставится символ операции разыме­нования *, чтобы получить доступ через указатель к значению переменной. А при вызове функции в нее в качестве аргумента должна передаваться не сама переменная, а ее адрес, получаемый с помощью операции адресации &.

Приведем пример той же рассмотренной ранее функции square, но с переда­чей параметра по ссылке с помощью указателя:

void square(int *); // Прототип функции вычисления квадрата

void square(int *а) // Заголовок функции

{

*а *= *а; // Изменение значения параметра

}

Вызов подобной функции может осуществляться, например, следующим образом:

int xl = 2;
square(&х1);

Задания для лабораторной работы №1.

Разработайте алгоритм, интерфейс пользователя, позволяющего вводить именованные исходные данные и вывод результатов, и программу решения задачи:

Вариант 1. Площади треугольника со сторонами a, b, c по формуле Герона.

,

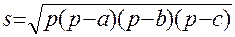где p = (a+ b + c)/2

Вариант 2. Площади поверхности усеченного конуса для заданных R, r,l.

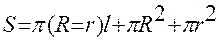
Вариант 3. Объема усеченного конуса для заданных R, r, h.

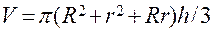
Вариант 4. Координаты центра тяжести трех материальных точек с массами m1, m2, m3 и координатами ( x1,y1), (x2,y2), (x3,y3).

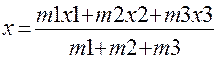
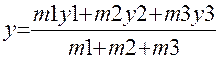
Вариант 5. Площади трапеции: где а и b — длины оснований; h — высота трапеции.

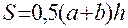
Вариант 6. Площади поверхности и объема цилиндра, где r – радиус основания, h – высота цилиндра.

; .

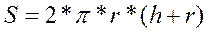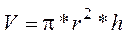Вариант 7. Объема и площади поверхности шара радиуса r.

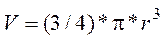
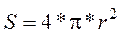
Вариант 8.. Объема полого цилиндра:

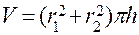
где 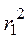радиус цилиндра, 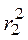радиус отверстия, h высота цилиндра.

Вариант 9. Объема конуса высотой h и основанием радиуса r

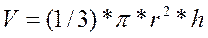
Вариант 10.Величину тока, протекающего через цепь из двух параллельно соединенных сопротивлений r₁ и r₂ ом при напряжении 5 вольт.

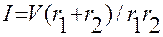
Вариант 11.Площадь треугольника, если известны координаты вершин его углов: a = x₁,y₁; b = x₂,y₂; c = x₃,y₃.

Вариант 12.Величину дохода по вкладу. Процентная ставка a% годовых и время хранения t дней задаются во время работы программы.

Вариант 13.Стоимость поездки на автомобиле на дачу (туда и обратно). Исходными данными являются: расстояние до дачи L км; количество бензина, которое потребляет автомобиль на 100 км пробега –v литров; цена одного литра бензина с – руб.

Вариант 14.Величину тока через цепь из двух последовательно соединенных сопротивлений.R₁ ,R₂ и напряжении сети - v в.

Вариант 15. Программу пересчета веса из фунтов в килограммы (один фунт — это 405,9 грамма).

Вариант 16. Программу пересчета расстояния из километров в версты (одна верста — это 1066,8 м).

Вариант 17. В треугольнике (см. рис.1.10, а) заданы две стороны а и b и угол между ними С. Вычислить сторону с, углы А и В и площадь треугольника.

Вариант 18. В треугольнике (см. рис.1.10, а) заданы сторона а и прилегающие к ней углы В и С. Вычислить стороны b, c угол A треугольника.

Вариант 19. В треугольнике (см. рис.1.10, а) заданы три стороны a, b и с. Вычислить величины углов A, B, C треугольника.

Вариант 20. В треугольнике (см. рис.1.10, а) заданы две стороны а, b и площадь S. Вычислить сторону c, углы A, B, C треугольника.

Вариант 21. В треугольнике (см. рис.1.10, а) заданы сторона а, угол С и площадь S. Вычислить стороны b, c и углы A, и B треугольника.

Вариант 22. В треугольнике (см. рис.1.10, а) заданы сторона b, угол А и радиус описанной окружности R. Вычислить стороны a, c и углы B и C треугольника.

Вариант 23. В треугольнике (см. рис.1.10, а) заданы углы А, В и радиус описанной окружности R. Вычислить стороны a, b, c и угол C треугольника.

Вариант 24. В треугольнике (см. рис.1.10, а) заданы стороны a, b и радиус описанной окружности R. Вычислить сторону c, и углы A, B, C треугольника.

Вариант 25. В треугольнике (см. рис.1.10, а) заданы стороны a, b и половина периметра р. Вычислить сторону c и углы A, B, C треугольника.

Вариант 26. В треугольнике (см. рис.1.10, а) заданы углы А, С и высота hb. Вычислить стороны a, b, c и угол B треугольника.

Вариант 27. В треугольнике (см. рис.1.10, а) заданы стороны а, с и высота hb. Вычислить сторону b и углы A, B, C треугольника.

Вариант 28. В треугольнике (см. рис.1.10, а) заданы угол А, сторона с и высота hb. Вычислить стороны a, b и углы B, C треугольника.

Вариант 29. В ромбе (см. рис.1.10, б) заданы координаты вершин ха, уа, хь, уь, хс, ус и xd, yd Вычислить стороны и диагонали ромба треугольника.

Вариант 30. В ромбе (см. рис.1.10, б) заданы сторона а и угол А. Вычислить диагонали и угол B ромба.

Дополнительный материал.

В формулах для треугольников (рис.1.10, а) используются следующие обозначения: a, b, c — стороны треугольника; А, В, С — углы треугольника, противолежащие соответствующим сторонам; ha, hb, hc — высоты треугольника, опущенные соответственно на стороны a, b и с; р, S —половина периметра и площадь треугольника; r, R — радиусы вписанной и описанной окружностей.

В формулах и заданиях для ромба (рис.1.10, б) используются следующие обозначения: а — сторона ромба; А, В, С, D — углы ромба; d1,d2 — диагонали ромба; р,S—периметр и площадь ромба.

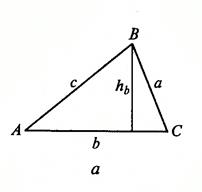
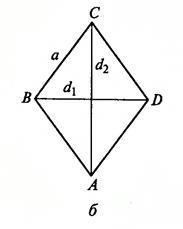
Рис.1.10. Обозначения элементов геометрических фигур к вариантам лабораторной работы №1: а — треугольник; б — ромб;

Приведем основные теоремы и формулы, необходимые для решения задач с треугольниками:

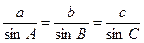- теорема синусов;

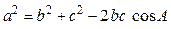- теорема косинусов;

;

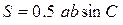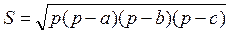- формула Герона;

;

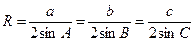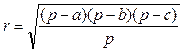
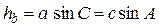
При расчете элементов трапеции кроме приведенных для треугольников соотношений используются формулы:

A+B=C+D=180 град; S = 0.5 (b+d)h.

Приложение 1

Математические функции

При работе с математическими функциями надо иметь ввиду, что файлы math.h и Math.hpp в C++ Bilderавтоматически не подключаются к модулю приложения. Поэтому для использования описанных в этих файлах функций необходимо вручную вводить директивы в раздел, предшествующий разделу описания классов заголовочного файла

# include <math.h>

# include <Math.hpp>.