Тепловой баланс парового котла

Тепловым балансом называют равенство между тепло­той, поступающей в котел в единицу времени, и теплотой, расхо­дуемой в нем на получение пара и тепловые потери. Тепловой баланс является частным случаем закона сохранения энергии.

Составим тепловой баланс для котла, не имеющего воздухо­подогревателя (Рис. 3.1). В топку котла поступает В, кг/с, топ­лива с теплотой сгорания , МДж/кг. Следовательно, при го­рении топлива в топке в еди­ницу времени будет выде­ляться , МДж/с (МВт), теплоты.

Для горения топлива необ­ходим воздух. Пусть энталь­пия холодного воздуха, требуе­мого для сжигания 1 кг топ­лива, составляет = , МДж/кг, где 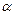– коэффициент избытка воз­духа; 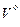– теоретически необ­ходимое количество воздуха для сжигания 1 кг топлива, м³/кг; – теплоемкость

Рис. К составлению теплового баланса

влажного воздуха, МДж/(м³Х Х°С); – температура хо­лодного воздуха, °С. Таким образом, с воздухом в топку вносится , МВт теплоты.

Топливо вводится в топку нагретым. Пусть энтальпия 1 кг нагретого топлива = МДж/кг, где – теплоемкость топлива, МДж/кг; – температура нагретого топлива, °С. Сле­довательно, нагретое топливо вносит в топку в единицу времени , МВт, теплоты.

Если топливо распыливается паромеханическими форсун­ками, то пар вносит добавочную теплоту , МВт, где – теплота пара, участвующего в распыливании топлива, МДж/кг.

Теперь рассмотрим расход теплоты в котле в единицу вре­мени. Пусть на подогрев воды и получение пара при сжигании 1 кг топлива затрачивается полезно используемая в котле теп­лота в количестве , МДж/кг. Ее полное количество составляет , МВт

В процессе работы котла имеются также тепловые потери. Самая большая из них – потеря теплоты с уходящими газами , где – эптальпия уходящих из котла газов при темпе­ратуре h °С. Другие потери теплоты: от химического недожога ( – потеря теплоты от неполноты горения углерода топ­лива, МДж/кг); от механической неполноты горения (механи­ческого недожога); , где – потеря теплоты от механиче­ской неполноты горения (зашлаковывания, уноса топлива и др.), МДж/кг; в окружающую среду ( – потеря теплоты на­гретыми стенками котла в окружающую среду, МДж/кг).

Если приравнять теплоту, поступающую в топку в единицу времени, теплоте, расходуемой за это же время полезно и в виде потерь, то получим уравнение теплового баланса, МВт,

.

(3.1)

На рис. 3.1 стрелками показаны составляющие уравнения (3.1). Это выражение можно представить в другом виде. Пере­несем энтальпию в правую часть уравнения и разделим обе части на В. Кроме того, условимся, что при сжигании жидко­го распыленного топлива потеря теплоты от меха­нической неполноты горе­ния = 0. Тогда фор­мула (3.1) получит вид, МДж/кг,

.

(3.2)

Рис. 3.2. Графическое изображение тепло­вого баланса котла, не имеющего возду­хоподогревателя

В этой формуле выражение – называют потерей теп­лоты с уходящими из котла дымовыми газами и обозначают , то есть

.

(3.3)

С учетом сказанного уравнение теплового баланса может быть представлено в следующем виде

.

(3.4)

Левую часть уравнения (3.4) называют располагаемой теп­лотой 1 кг рабочей массы топлива и обозначают . Оконча­тельно уравнение теплового баланса записывается так

.

(3.5)

На рис. 3.2 дано графическое изображение теплового ба­ланса парового котла.

Выражение (3.5) получено для парового котла, не имеющего воздухоподогревателя, однако оно остается справедливым и для котла, оборудованного газовым воздухоподогревателем. Для того чтобы пользоваться уравнением (3.5), надо рассчитать ве­личины, входящие в это уравнение.

Определение величин, входящих в левую часть, с учетом изло­женного ранее, не вызывает затруднений: . Для мазутов МДж/кг; ; поскольку МДж/(кг∙°С), а , то МДж/кг. Величина очень мала, поэтому ею можно пренебречь. Таким образом, для мазута среднего состава = 40,6 МДж/кг.

Далее рассмотрим определение величин, входящих в пра­вую часть уравнения (3.5), начиная с полезно используемой теп­лоты .