Средняя линия треугольника (определение).
 |
2.ДОКАЖИТЕ, ЧТО У РАВНОБОКОЙ ТРАПЕЦИИ УГЛЫ ПРИ ОСНОВАНИИ РАВНЫ.
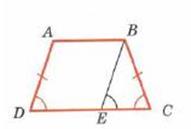 | Дано: ΔАВСД-данная трапеция |
| Док-ть ∟D=∟C | |
Доказательство  |
‘
Билет№15.
1. ОПРЕДЕЛЕНИЕ ТРАПЕЦИИ. ВИДЫ ТРАПЕЦИИ.
 Все трапеции можно разделить на три вида: - равнобедренные трапеции; - прямоугольные трапеции; - произвольные трапеции. Равнобедренные трапеции — это трапеции, у которых боковые стороны равны. Прямоугольные трапеции — это трапеции, у которых одна боковая сторона перпендикулярна основаниям. Произвольные трапеции — все остальные трапеции, которые не являются ни равнобедренными, ни прямоугольными. Схематически виды трапеций можно изобразить так: Все трапеции можно разделить на три вида: - равнобедренные трапеции; - прямоугольные трапеции; - произвольные трапеции. Равнобедренные трапеции — это трапеции, у которых боковые стороны равны. Прямоугольные трапеции — это трапеции, у которых одна боковая сторона перпендикулярна основаниям. Произвольные трапеции — все остальные трапеции, которые не являются ни равнобедренными, ни прямоугольными. Схематически виды трапеций можно изобразить так:  |
ДОКАЖИТЕ, ЧТО ЛЮБЫЕ ДВЕ МЕДИАНЫ ТРЕУГОЛЬНИКА В ТОЧКЕ ПЕРЕСЕЧЕНИЯ ДЕЛЯТСЯ В ОТНОШЕНИИ 2:1,СЧИТАЯ ОТ ВЕРШИНЫ.
И ВСЕ ТРИ МЕДИАНЫ ТРЕУГОЛЬНИКА ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ.
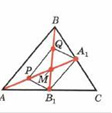 | Дано: ΔАВС-треугольник АА1, ВВ1-медианы треугольника АА1∩ВВ1=М |
| Док-ть АМ:МА1=2:1 | |
 Доказательство Доказательство |
Билет№16.
1. ОПРЕДЕЛЕНИЕ КВАДРАТА. СВОЙСТВА КВАДРАТА.
 |
2.ТЕОРЕМА ПИФАГОРА (ДОКАЗАТЕЛЬСТВО).
Теорема:  | |
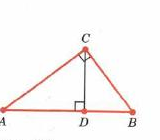 | Дано: ΔАВС-прямоугольный треугольник ∟С= 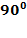 |
Док-ть 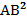 = = 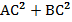 | |
Доказательство  |
Билет№17.
1. ОПРЕДЕЛЕНИЕ РОМБА. СВОЙСТВА РОМБА.
  |
2.НЕРАВЕНСТВО ТРЕУГОЛЬНИКА (ДОКАЗАТЬ ТЕОРЕМУ).
Теорема:  | |
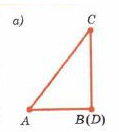 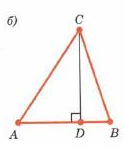 | Дано: А,В,С-данные точки |
Док-ть 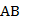 < < 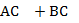 | |
Доказательство   |
Билет№18.
ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНИКА. СВОЙСТВА ПРЯМОУГОЛЬНИКА.
  |
2. ВЫВОД ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ УГЛОВ 30º ,45º, 60º.
Для любого острого угла а sin (90° — а)=cos а, cos (90° — а)=sin а. Доказательство. Пусть ABC — прямоугольный треугольник с острым углом а при вершине А (рис. 160). Тогда острый угол при вершине В равен 90° — а. По определению 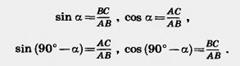 Из второго и третьего равенств получаем sin (90° — а) = cos а. Из первого и четвертого равенств получаем cos (90° — a) = sin а. Теорема доказана. Из второго и третьего равенств получаем sin (90° — а) = cos а. Из первого и четвертого равенств получаем cos (90° — a) = sin а. Теорема доказана. 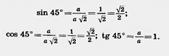 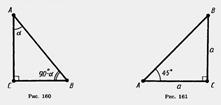 Найдем синус, косинус и тангенс угла 45°. Для этого построим прямоугольный треугольник с острым углом 45° (рис. 161). Второй его острый угол тоже равен 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны а. По теореме Пифагора гипотенуза будет Найдем синус, косинус и тангенс угла 45°. Для этого построим прямоугольный треугольник с острым углом 45° (рис. 161). Второй его острый угол тоже равен 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны а. По теореме Пифагора гипотенуза будет 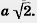 . Находим: . Находим: 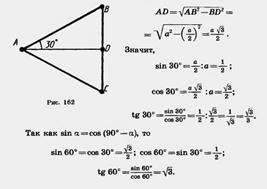 Найдем синус, косинус и тангенс угла 30°. Возьмем равносторонний треугольник ABC (рис. 162). Проведем в нем медиану AD. Она будет биссектрисой и высотой. Поэтому треугольник ABD прямоугольный с острым углом при вершине А, равным 30°. Пусть а — сторона равностороннего треугольника. Тогда BD= Найдем синус, косинус и тангенс угла 30°. Возьмем равносторонний треугольник ABC (рис. 162). Проведем в нем медиану AD. Она будет биссектрисой и высотой. Поэтому треугольник ABD прямоугольный с острым углом при вершине А, равным 30°. Пусть а — сторона равностороннего треугольника. Тогда BD= 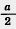 . По теореме Пифагора . По теореме Пифагора |
Билет№19.
1 .ОПРЕДЕЛЕНИЕ ЧЕТЫРЕХУГОЛЬНИКА.
 |
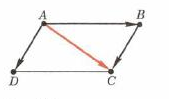
2.СЛОЖЕНИЕ ВЕКТОРОВ (ДОКАЗАТЕЛЬСТВО).ПРАВИЛО ТРЕУГОЛЬНИКА И ПРАВИЛО ПАРАЛЛЕЛОГРАММА (РАССМОТРЕТЬ СПОСОБЫ ПОСТРОЕНИЯ).


Билет№20.
1.ОПРЕДЕЛЕНИЕ И СВОЙСТВА ПАРАЛЛЕЛОГРАММА.
   |
 2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ (ОПРЕДЕЛЕНИЕ). ДОКАЗАТЬ ТЕОРЕМУ О СКАЛЯРНОМ ПРОИЗВЕДЕНИИ ВЕКТОРОВ.
2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ (ОПРЕДЕЛЕНИЕ). ДОКАЗАТЬ ТЕОРЕМУ О СКАЛЯРНОМ ПРОИЗВЕДЕНИИ ВЕКТОРОВ.

