Пересечение прямой и окружности.
Пересечение прямой с окружностью Рассмотрим вопрос о пересечении прямой с окружностью. Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось х (рис. 179). Тогда уравнением окружности будет x'2 + y2=R2, а уравнением прямой x = d. Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений x'2 + y2=R2, x = d имела решение. И обратно: всякое решение этой системы дает координаты X, у точки пересечения прямой с окружностью. Решая нашу систему, получим:   Из выражения для у видно, что система имеет два решения, т. е. окружность и прямая имеют две точки пересечения, если R>d (рис. 179,а). Система имеет одно решение, если R=d (рис. 179,в). В этом случае прямая и окружность касаются. Система не имеет решения, т. е. прямая и окружность не пересекаются, если R<.d (рис. 179, в). Из выражения для у видно, что система имеет два решения, т. е. окружность и прямая имеют две точки пересечения, если R>d (рис. 179,а). Система имеет одно решение, если R=d (рис. 179,в). В этом случае прямая и окружность касаются. Система не имеет решения, т. е. прямая и окружность не пересекаются, если R<.d (рис. 179, в). |
2.ДОКАЖИТЕ, ЧТО ЕСЛИ У ПАРАЛЛЕЛОГРАММА ДИАГОНАЛИ ПЕРПЕНДИКУЛЯРНЫ, ТО ОН ЯВЛЯЕТСЯ РОМБОМ.
 | Дано: АВСD-параллелограмм АС┴BD |
| Док-ть: АВСD-ромб | |
Доказательство:  |
БИЛЕТ№9.
1.ЗНАЧЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА НЕКОТОРЫХ УГЛОВ (45°, 30°,60°).
Для любого острого угла а sin (90° — а)=cos а, cos (90° — а)=sin а. Доказательство. Пусть ABC — прямоугольный треугольник с острым углом а при вершине А (рис. 160). Тогда острый угол при вершине В равен 90° — а. По определению 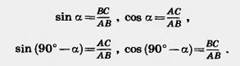 Из второго и третьего равенств получаем sin (90° — а) = cos а. Из первого и четвертого равенств получаем cos (90° — a) = sin а. Теорема доказана. Из второго и третьего равенств получаем sin (90° — а) = cos а. Из первого и четвертого равенств получаем cos (90° — a) = sin а. Теорема доказана. 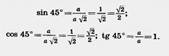 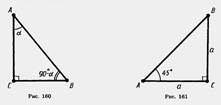 Найдем синус, косинус и тангенс угла 45°. Для этого построим прямоугольный треугольник с острым углом 45° (рис. 161). Второй его острый угол тоже равен 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны а. По теореме Пифагора гипотенуза будет Найдем синус, косинус и тангенс угла 45°. Для этого построим прямоугольный треугольник с острым углом 45° (рис. 161). Второй его острый угол тоже равен 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны а. По теореме Пифагора гипотенуза будет 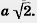 . Находим: . Находим: 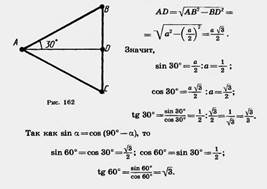 Найдем синус, косинус и тангенс угла 30°. Возьмем равносторонний треугольник ABC (рис. 162). Проведем в нем медиану AD. Она будет биссектрисой и высотой. Поэтому треугольник ABD прямоугольный с острым углом при вершине А, равным 30°. Пусть а — сторона равностороннего треугольника. Тогда BD= Найдем синус, косинус и тангенс угла 30°. Возьмем равносторонний треугольник ABC (рис. 162). Проведем в нем медиану AD. Она будет биссектрисой и высотой. Поэтому треугольник ABD прямоугольный с острым углом при вершине А, равным 30°. Пусть а — сторона равностороннего треугольника. Тогда BD= 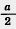 . По теореме Пифагора . По теореме Пифагора |
2.ДОКАЖИТЕ, ЧТО ЕСЛИ ДИАГОНАЛИ ПРЯМОУГОЛЬНИКА ПЕРЕСЕКАЮТСЯ ПОД ПРЯМЫМ УГЛОМ, ТО ОН ЯВЛЯЕТСЯ КВАДРАТОМ.
 | Дано: АВСD-прямоугольник АС┴BD |
| Док-ть АВСD-квадрат | |
Доказательство  |
БИЛЕТ№10.
1.ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА.
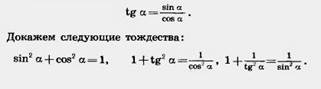 Одно тождество мы уже знаем: Одно тождество мы уже знаем: 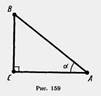 Возьмем любой прямоугольный треугольник ABC с углом при вершине А, равным а. По теореме Пифагора ВС2 + АС2 = АВ2. Разделим обе части равенства на АВ2. Получим: Возьмем любой прямоугольный треугольник ABC с углом при вершине А, равным а. По теореме Пифагора ВС2 + АС2 = АВ2. Разделим обе части равенства на АВ2. Получим: 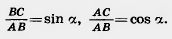 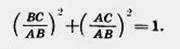 Но . Таким образом,sin2a + cos2 а = 1. Это равенство есть тождество. Оно верно для любого острого угла а. Чтобы получить второе тождество, разделим обе части полученного тождества на cos2 а. Получим: Но . Таким образом,sin2a + cos2 а = 1. Это равенство есть тождество. Оно верно для любого острого угла а. Чтобы получить второе тождество, разделим обе части полученного тождества на cos2 а. Получим: 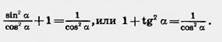 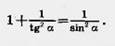 Если обе части тождества sin2 а + cos2а = 1 разделить на sin2а, то получим третье тождество : Значение этих тождеств заключается в том, что они позволяют, зная одну из величин sin а, cos а или tg а, найти две другие. Если обе части тождества sin2 а + cos2а = 1 разделить на sin2а, то получим третье тождество : Значение этих тождеств заключается в том, что они позволяют, зная одну из величин sin а, cos а или tg а, найти две другие. |
ТЕОРЕМА ФАЛЕСА.
| Теорема: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне. | |
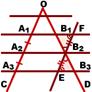 | Дано: ∟COD A1B1 ∥ A2B2 ∥ A3B3, A1, A2, A3 ∈ OC, B1, B2, B3 ∈ OD, A1A2=A2A3. |
| Док-ть B1B2=B2B3. | |
| Доказательство 1) Через точку B2 проведем прямую EF, EF ∥ A1A3. 2) Рассмотрим четырехугольник A1FB2A2. - A1F ∥ A2B2 (по условию), - A1A2 ∥ FB2 (по построению).Следовательно, A1FB2A2 — параллелограмм (по определению). По свойству противолежащих сторон параллелограмма, A1A2=FB2. 3) Аналогично доказываем, что A2B2EA3 — параллелограмм и A2A3=B2E. 4) Так как A1A2=A2A3 (по условию), то FB2=B2E. 5) Рассмотрим треугольники B2B1F и B2B3E. - FB2=B2E (по доказанному), - ∠B1B2F=∠B2EB3 (как вертикальные), - ∠B2FB1=∠B2EB3 (как внутренние накрест лежащие при A1B1 ∥ A3B3 и секущей EF). Следовательно, треугольники B2B1F и B2B3E равны (по стороне и двум прилежащим к ней углам). Из равенства треугольников следует равенство соответствующих сторон: B1B2=B2B3. Что и требовалось доказать. |
Билет№11.
1.СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И УГЛАМИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ (ОПРЕДЕЛЕНИЕ).
 |
2.ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРАПЕЦИИ.
Теорема:  | |
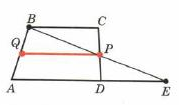 | Дано: ΔАВСД-данная трапеция QP-средняя линия |
| Док-ть QP║ BC, QP║AD QP =1/2 (BC+ AD) | |
Доказательство   |
Билет№12.
1.ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ (ОПРЕДЕЛЕНИЕ).
 |
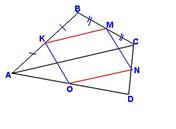
2. ДОКАЖИТЕ,ЧТО СЕРЕДИНЫ СТОРОН ЧЕТЫРЕХУГОЛЬНИКА ЯВЛЯЮТСЯ ВЕРШИНАМИ ПАРАЛЛЕЛОГРАММА.
 | Дано: ΔАВС-треугольник ЕД-средняя линия |
| Док-ть ЕД║АВ,ЕД=1/2АВ | |
| Доказательство: Проведем диагональ АС в четырехугольнике АВСД.АС разбивает четырехугольник на 2 треугольника АВС и АДС. Проведем средние линии в треугольниках КМ и ОN. КМ - средняя линия ΔАВС(по определению), тогда КМ = АС/2 и КМ ║ АС. ON- средняя линия ΔADC, значит ON = AC/2 и ON ║АС Получаем, что KM=ON и KM параллельна ON(это признак!) Если две стороны четырехуг. равны и параллельны, то четырехуг. - параллелограмм. Значит KMNO параллелограм. |
Билет№13.
1.СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА (ОПРЕДЕЛЕНИЕ).
 |
2.ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРЕУГОЛЬНИКА.
Теорема:  | |
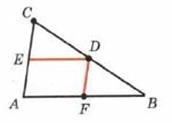 | Дано: ΔАВС-треугольник ЕД-средняя линия |
| Док-ть ЕД║АВ,ЕД=1/2АВ | |
Доказательство  |
Билет№14.
