Взаимное расположение двух прямых в пространстве
Если две прямые пересекаются или параллельны, то они лежат в одной плоскости. Однако в пространстве две прямые могут быть расположены так, что они не лежат в одной плоскости, то есть не существует такой плоскости, которая проходит через обе эти прямые. Ясно, что такие прямые не пересекаются и не параллельны.
В пространстве рассматриваются три случая возможного расположения двух прямых. Две прямые в пространстве могут:
1. Лежать в одной плоскости и иметь общую точку;
2. Лежать в одной плоскости и не иметь общих точек;
Не лежать в одной плоскости и, следовательно, не иметь общих точек.
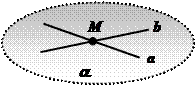Определение: Две прямые называются пересекающимися, если они имеют общую точку.
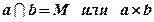
Определение: Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек или совпадают.
 |
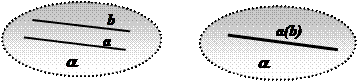Теоремы:
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Если две прямые параллельны третьей прямой, то они параллельны.
Замечание: Теоремы о параллельных прямых в пространстве примем без доказательства.
 |
Определение: Две прямые называются скрещивающимися, если они не пересекаются и не параллельны (не лежат в одной плоскости).
Обозначение: a · b
ПРИЗНАК СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ
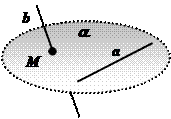
Теорема: Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые скрещиваются.
Дано: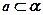 
; 
; 
.
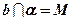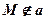Доказать: a · b
Доказательство: (методом от противного)
Предположим противоположное тому, что требуется доказать, то есть, что данные прямые пересекаются или параллельны: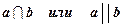 
.
Через две пересекающиеся или параллельные прямые можно провести единственную плоскость, следовательно, существует некоторая плоскость, в которой лежат данные прямые: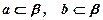 
.
По условию теоремы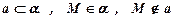 
.
По предположению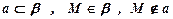 
.
Из условия теоремы и из предположения следует, что обе плоскости проходят через прямую «а» и не принадлежащую ей точку М. А так как через прямую и не принадлежащую ей точку можно провести одну и только одну плоскость, следовательно, плоскости совпадают.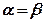 
.
По предположению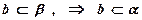 
.
По условию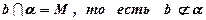 
.
Получили противоречие с условием теоремы, следовательно, предположение не верно, а верно то, что требовалось доказать, то есть прямые скрещиваются: a · b.
Вывод:
1. Через скрещивающиеся прямые нельзя провести плоскость.
2. Чтобы доказать, что две данные прямые скрещиваются, надо назвать (задать) плоскость, которой одна из этих прямых принадлежит, а другая прямая её пересекает в точке, не принадлежащей первой прямой.
 |
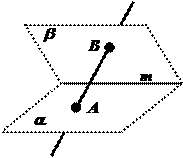Пример: Известно, что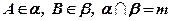 
. Возможны ли какие-либо случаи взаимного расположения прямых АВ и т, кроме случая, изображенного на рисунке?
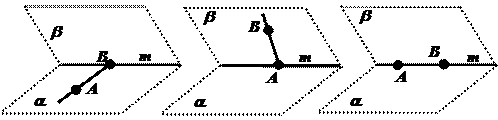
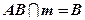
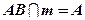
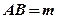
Упражнения: