Величины для различных случаев посадки судна

Для определения посадки судна с использованием системы уравнений (2.1) необходимо иметь значения погруженного объема (V) и координат центра величины (x_с, z_с). Эти показатели относятся к элементам теоретического чертежа (рис. 1.10); их также принято называть – основные элементы плавучести.

2.4.1. Определение V, x_c, z_c при посадке судна прямо и на ровный киль

Расчет V при заданной осадке(Т), может быть выполнен с использованием:

– ординат теоретического чертежа корпуса судна;

– строевой по шпангоутам (рис. 1.11);

– строевой по ватерлиниям (см. зависимость S = f(z) на рис. 1.10).

Расчет V с использованием ординат теоретического чертежа и строевых выполняется по форме табл. 1.3.

Координаты x_с и z_с центра величины рассчитываются по форме табл. 1.4 (см. п.1.3 пособия).

При решении производственной задачи определения водоизмещения по осадке или наоборот – осадки по водоизмещению, используют кривую объемного водоизмещения (V) (рис. 2.9).

Для значительной части морских судов и смешанного (река-море) плавания кривая V, при малых осадках, расположена почти вертикально, а затем постепенно отходит от вертикальной оси. Это обусловлено тем, что площадь нулевой ватерлинии у этих судов равна нулю, либо мала (см. рис. 2.9). На участке, где судно имеет вертикальные борта, S практически не зависит от осадки и кривая V приближается к наклонной прямой линии.

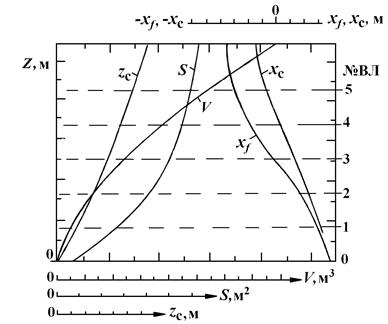Рис. 2.9. Кривые плавучести

В эксплуатационной практике широко используется график – «грузовой размер».

Грузовой размер – это графическая зависимость массового водоизмещения (D) от осадки (рис. 2.10). соотношение между V и D определяется формулой 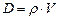, где r – плотность воды.

Если судно эксплуатируется в пресной и морской воде, то для него рассчитываются кривые 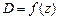, соответствующие этим условиям.

Грузовой размер позволяет, например, определить изменение осадки (DТ_гр) в результате приема груза массой Р_гр или изменение осадки (DТ) судна, имеющего массовое водоизмещение D_гр, при его переходе из реки в море (см. рис. 2.10)

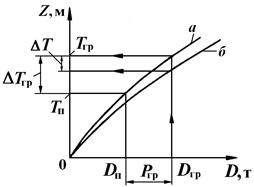Рис. 2.10. Грузовой размер:

а) – пресная вода; б) – морская вода

Наряду с грузовым размером на судне пользуются грузовой шкалой (рис. 2.11).

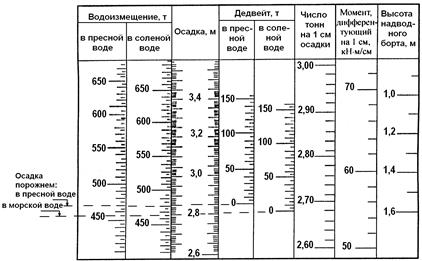Рис. 2.11. Грузовая шкала

Она содержит шкалы взаимосоответствующих значений следующих показателей по судну: осадки; массового водоизмещения; дедвейта (полной грузоподъемности); количества тонн, изменяющих осадку на 1 см; момента создающего дифферент в 1 см; высоты надводного борта.

Грузовая шкала в судовых условиях широко используется для определения массы принятого или снятого груза.

Грузовой размер и грузовая шкала рассчитываются для посадки судна прямо и на ровный киль; такая посадка определяется одним показателем – Т.

Посадка судна в процессе его эксплуатации (необходимая для последующего решения задач по грузовому размеру и грузовой шкале), определяется с использованием шкал углубления, которые наносятся на обоих бортах на носу, корме и в районе миделя (рис. 2.12).

В носовой оконечности шкала углубления изображается по обводу форштевня, а в корме – вертикально; средняя шкала наносится вблизи миделя. На схеме также показываются носовой (НП) и кормовой (КП) перпендикуляры.

Высота наносимых цифр – 10 см; число на шкале указывает углубление в дециметрах. Число соответствует углублению по нижний уровень его записи на шкале.

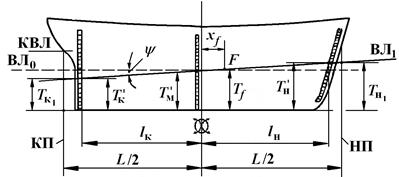Рис. 2.12. Шкалы углубления:

НП – носовой перпендикуляр; КП – кормовой перпендикуляр

Шкалы углубления дают габаритное погружение, т.е. учитывают конструкции, закрепленные на корпусе и выступающие за основную плоскость. На большинстве водоизмещающих судов такие конструкции отсутствуют; на этих судах шкалы углубления показывают осадку судна, т.е. отстояние основной плоскости от поверхности воды, например, в районе миделя ( 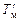, см. рис. 2.12).

Если судно имеет крен, то осадку (углубление) следует принимать как среднее по значениям, снятым (считанным) со шкал на обоих бортах. Угол крена может быть определен по разности осадок на правом 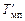и левом 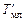бортах, считанных на миделе

,

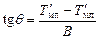где В – ширина корпуса в месте расположения шкал углубления.

Схема размещения шкал углубления имеется в «Информации об остойчивости и непотопляемости судна», которая выдается на судно [6] [7].

С использованием грузового размера и грузовой шкалы в эксплуатационной практике решаются задачи, как при прямой посадке судна, так и при малых значениях дифферента (y < 3°).

При наличии дифферента со шкал углубления судна снимаются значения 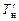, 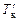и осадка на миделе ( 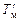); со схемы размещения шкал снимаются отстояния чисел на шкалах углубления от миделя (l_н, l_к, см. рис. 2.12). С использованием считанных показателей 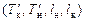рассчитывается осадка Т_f по шпангоуту, в плоскости которого находится поперечная ось вращения судна при продольном наклонении. Эта ось проходит через центр тяжести площади ватерлинии ВЛ₀ (т. F, см. рис. 2.12). Исходя из геометрического посыла, нетрудно получить формулу

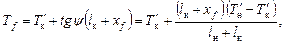(2.2)

где

xf

–

абсцисса центра тяжести площади ватерлинии ВЛ0; определяется по графику рис. 2.8 с использованием снятого значения осадки на миделе .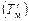

По полученному значению Т_f с использованием грузового размера или грузовой шкалы определяется значение D, а затем V.

В тех случаях, когда требуется определить водоизмещение с возможно меньшей погрешностью, к его значению, снятому с грузовой шкалы или грузового размера, вводят поправку. Последняя учитывает следующее обстоятельство. Грузовая шкала и грузовой размер строятся в предположении, что корпус судна является абсолютно жестким телом. Однако, в частности, при проведении погрузки (выгрузки) судна он может деформироваться.

Поправка на изгиб корпуса приближенно определяется выражением

,

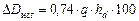где	q	–	число тонн, изменяющих осадку на 1 см (рис. 2.11);
	hd	–	стрелка кривизны корпуса на миделе, м.

Последняя рассчитывается по формуле

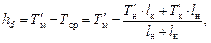(2.3)

где		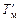–	осадка корпуса на миделе, снятая по миделевой шкале осадок;
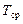		–	средняя осадка на миделе, получаемая расчетом, исходя из осадок, считанных с носовой и кормовой шкал (см. формулу (2.3);
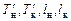	–	геометрические характеристики, представленные на рис. 2.12.

Окончательное водоизмещение (D_пол) судна

,

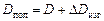где	D	–	водоизмещение по грузовой шкале при Т = Тf (см. формулу (2.2);
	DDизг	–	добавка на влияние изгиба корпуса.

Координаты центра величины (x_с, z_с) для судна, имеющего посадку прямо и на ровный киль определяются при известном значении V или Т по графику рис. 2.9.

2.4.2. Определение V, x_с, z_с при посадке судна с креном и дифферентом

Выше рассмотрен случай посадки судна прямо и на ровный киль, когда положение судна определяется одним параметром – осадкой (Т). Зависимостями, представленными на рис. 2.9, 2.10 и 2.11, пользуются для решения задач, как при посадке прямо и на ровный киль, так и при малых значениях дифферента (y < 3°).

Рассмотрим определение основных элементов плавучести при посадке судна с большим дифферентом.

Посадка судна прямо и с дифферентом

В этом случае для выполнения расчетов используется масштаб Бонжана (рис. 2.13).

Такой график представляет собой совокупность кривых, каждая из которых определяет зависимость погруженной площади шпангоута (при q = 0) от его углубления. Масштаб Бонжана строится для 21 теоретического шпангоута; на рис. 2.13, для упрощения, кривые погруженных площадей показаны только для четных шпангоутов (0, 2, 4 и т.д.).

Масштаб Бонжана позволяет вычислять V, х_с, z_c при посадке с любым дифферентом.

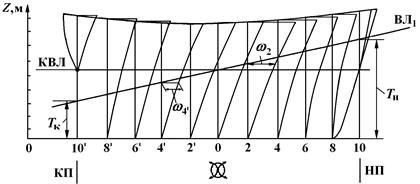Рис. 2.13. Масштаб Бонжана

Ватерлиния на масштаб Бонжана наносится в виде прямой по заданным осадкам носом Т_н и кормой Т_к, которые откладываются на носовом (НП) и кормовом (КП) перпендикулярах (см. рис. 2.13).

Точки пересечения этой прямой с вертикалями определяют уровень погружения каждого из шпангоутов. Измеряя по горизонтали на уровне этих точек отрезки до соответствующих кривых, получают, с учетом шкалы соответствия линейного размера и площади, погруженные площади шпангоутов ( 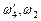на рис. 2.13). Найденные площади являются ординатами строевой по шпангоутам (см. рис. 1.11); с их использованием рассчитывают V (см. табл. 1.3) и x_с (см. формулу (1.29).

Масштаб Бонжана позволяет определить и аппликату центра величины (z_с); такой расчет, ввиду его сложности, в пособии не представлен.

Систематические вычисления на основе масштаба Бонжана выполняют еще в процессе проектирования судна; по их результатам строят диаграммы (рис. 2.14 и 2.15).

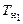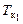На диаграмме Фирсова (см. рис. 2.14) изображают два семейства кривых: постоянного водоизмещения (V) и постоянного значения абсциссы центра величины (x_с). На координатных осях даются значения осадки носом (Т_н) и кормой (Т_к) на перпендикулярах (НП и КП, см. рис. 2.13). Диаграмма Фирсова позволяет по осадкам и без каких-либо дополнительных вычислений определить соответствующие V и x_c (см. рис. 2.14, т.А). по диаграмме аппликат (рис. 2.14) аналогично можно определить значение z_c.

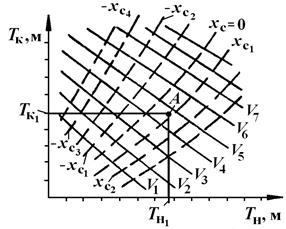Рис. 2.14. Диаграмма Г.А. Фирсова

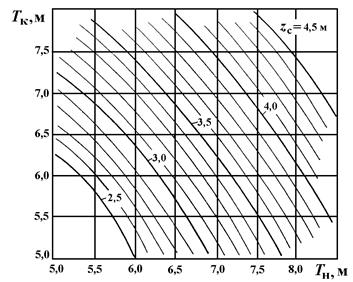Рис. 2.15. Диаграмма аппликат центра величины

Если, в итоге загрузки (разгрузки) судна, со шкал углубления считаны осадк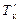и и 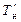, то, затем, по диаграмме Фирсова можно определить соответствующие значения V и x_c, а по диаграмме аппликат (см. рис. 2.15) – значение z_c. Для «входа» в эти диаграммы, исходя из 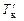и 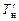выполняется расчет осадки судна по носовому перпендикуляру ( 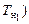и по кормовому ( 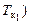с использованием формул

,

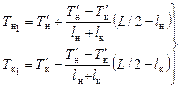(2.4)

где		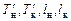–	геометрические показатели представленные на рис. 2.12;
	L	–	длина корпуса между носовым и кормовым перпендикулярами (длина КВЛ).

В эксплуатационной практике нередко решается задача об определении осадки носом и кормой после загрузки или разгрузки судна. Для этого выполняется расчет ожидаемой массы судна D¢ и абсциссы его центра тяжести 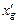по форме табл. 2.1. затем с диаграммы Фирсова (см. рис. 2.14) по точке А, удовлетворяющей условиям 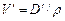и 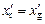, где r – плотность воды, снимаются приближенные значения осадки носом и кормой на перпендикулярах ( ).

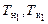Посадка судна с креном и дифферентом

В этом случае для вычисления водоизмещения V и координат центра величины (x_c, z_c) используют интегральные кривые Власова (рис. 2.16).

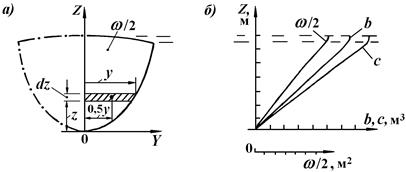Рис. 2.16. Полушпангоут (а) и интегральные кривые Власова (б)

По каждому шпангоуту, для половины его площади (см. рис. 2.16, а), определяются: площадь погружной части (w/2), а также статический момент этой площади относительно оси 0z (обозначение момента – «b») и статический момент площади относительно оси 0У (обозначение – «с») (см. рис. 2.16, б). Зависимости показателей w/2, b, c от координат У и z шпангоута имеют вид

.

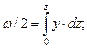
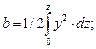
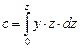Значения показателей w/2, b, c используются для последующего определения, с учетом крена и дифферента, полной погруженной площади шпангоута (w_i), статического момента этой площади относительно оси 0z (обозначение – В_i) и статического момента площади шпангоута относительно оси 0У (c_i).

В итоге, для судна имеющего крен и дифферент, расчет V выполняется с использованием строевой по шпангоутам (ряд w_i) (см. рис. 1.11 и формулу (1.27); для расчета х_с используются w_i и формула (1.29); для расчета у_с используются значения В_i, а расчета z_c – с_i.

Ввиду сложности, расчет V, х_с, z_c на основе кривых Власова здесь не представлен; подробнее об этом см. [ ].

Установлено [3], что влияние угла крена на V, z_c, х_с мало, поэтому диаграммой Фирсова (рис. 2.14) и диаграммой аппликат центра величины, которые рассчитываются при q = 0, можно пользоваться при посадке судна с креном (q < 10°) и дифферентом.