Основные свойства числовых неравенств

1) Если a>b, то b<a.

2) Если a>b и b>c, то a>c (свойство транзитивности).

3) Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство: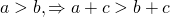

4) Если обе части верного неравенства умножить на одно и то же положительное число, то получится верное неравенство:

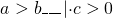
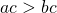
Если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство:

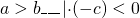
5) Если a>b и c>d, то a+c>b+d. Неравенства одного смысла можно складывать.

6) Если a,b,c,d — положительные числа и a>b,c>d, то ac>bd.

При умножении неравенств одного смысла, у которых левые и правые части — положительные числа, получается неравенство того же смысла.

7) Если a и b — неотрицательные числа и a<b то aⁿ<bⁿ, где n — натуральное число.

Если обе части неравенства — неотрицательные числа, то их можно возвести в одну и ту же натуральную степень, при этом получается неравенство того же смысла.

Линейным неравенством называется неравенство, которое дано или преобразуемо в формуax>bилиax<b, так жеax≥bилиax≤b,
гдеa,b— числа иx— переменная.

Пример:

a−5>0 a>5 Ответ:a∈(5;+∞)

−2y−100<0 −2y<100|:(−2) (знак неравенства меняется на противоположный) y>100:(−2) y>−50 Ответ:y∈(−50;+∞)

−3c≥−15|:(−3) (знак неравенства меняется на противоположный) c≤−15:(−3)c≤5Ответ:c∈(−∞;5]

Обрати внимание!

Решая линейные, да и не только линейные, неравенства, следует помнить, что при умножении или делении неравенства на положительное число знак неравенства сохраняется, а при умножении или делении неравенства на отрицательное число знак неравенства меняется на противоположный.

Решением неравенства с переменной называют значение переменной, которое обращает неравенство с переменной в верное числовое неравенство.

Решить неравенство — это значит найти все его решения или доказать, что их нет.

Дополнительно:

Билет № 12. Вопрос 2.

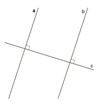Две прямые a и b на плоскости, которые не пересекаются, называются параллельными и обозначаются a∥b.

Один из признаков параллельности прямых в плоскости гласит:

1. Признак. Если две прямые на плоскости перпендикулярные одной и той же прямой, то они параллельны.

Для рассмотрения других признаков надо ознакомиться с некоторыми видами углов:

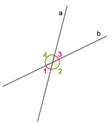1) Вспомним, что нам известны названия и свойства углов, которые образуют две пересекающиеся прямые

Вертикальные углы равны:∡1=∡3;∡2=∡4

Сумма смежных углов1800:∡1+∡2=∡2+∡3=∡3+∡4=∡4+∡1=1800

2) Если две прямые пересекает третья прямая, то углы называются так:

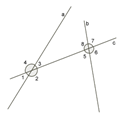
Накрест лежащие углы ∡3 и ∡5;∡2 и ∡8

Соответственные углы ∡1 и ∡5;∡4 и ∡8;∡2 и ∡6;∡3 и ∡7

Односторонние углы∡3и∡8;∡2и∡5

Эти углы помогут определить параллельность прямых a и b.

2. Признак. Если при пересечении двух прямых третьей секущей:

накрест лежащие углы равны, или

соответственные углы равны, или

сумма односторонних углов равна 180°, то прямые параллельны.

Признак параллельных прямых действует и как свойство параллельных прямых.

При пересечении двух параллельных прямых третьей секущей:

- накрест лежащие углы равны,

- соответственные углы равны,

- сумма односторонних углов равна 180°.

Признак - это некоторый факт, благодаря которому мы устанавливаем справедливость интересующего нас суждения о некотором объекте.

Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две прямые параллельны.

Свойство - если мы уверены в справедливости суждения, мы формулируем свойство объекта.

Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.

Аксиома, в свою очередь, такая истина, которую не надо доказывать. В каждой науке есть свои аксиомы, на справедливость которых строят все дальнейшие суждения и их доказательства.

Аксиома параллельных прямых.

В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.

Иногда эту аксиому называют как одно из свойств параллельных прямых, но на справедливости этой аксиомы строятся многие доказательства в геометрии.

Другие свойства параллельных прямых.

1. Если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.

2. Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.