Теоремы о площади треугольника
Билет № 1. Вопрос 1.
Необходимость появления обыкновенных дробей обусловлена тем, что операция деления над натуральными числами была выполнима не всегда.
Так, например, 5:2 = 2,5. Число 2, 5 – не является ни натуральным, ни целым.
Обыкновенной дробью называется число вида  где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем.
где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем.
Если n = 1, то дробь имеет вид  и её часто записывают просто m. Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.
и её часто записывают просто m. Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.
| Основное свойство дроби Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной. |
С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например,  (здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например,
(здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например,  – несократимая дробь.
– несократимая дробь.
Справедливо следующее утверждение:
Обыкновенная дробь  называется правильной, если её числитель меньше её знаменателя, то есть m < n. Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m > n.
называется правильной, если её числитель меньше её знаменателя, то есть m < n. Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m > n.
Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.  |
Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например,  Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например,
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например,  Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.
Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть
 |
Если знаменатели данных дробей разные, то дроби нужно сначала привести к общему знаменателю, а потом поступить, как описано выше.
Вычитание. Если две дроби имеют одинаковые знаменатели, то
 |
Если знаменатели данных дробей различны, то сперва приводят дроби к общему знаменателю, а потом вычитают их по вышеприведённой формуле.
Умножение. Произведение двух дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению их знаменателей, то есть
 |
Деление. Деление дробей осуществляют следующим образом:
 |
В случае умножения и деления смешанных чисел всегда удобно переходить к неправильным дробям.
Билет № 1. Вопрос 2.
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Свойства параллелограмма
 1. Противоположные стороны параллелограмма попарно равны
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
 3.Сумма смежных (соседних) углов параллелограмма равна 180 градусов
3.Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
 5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
 6.Биссектриса отсекает от параллелограмма равнобедренный треугольник
6.Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны:
2.Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
4.Противоположные стороны равны и параллельны
Билет № 2. Вопрос 1.
Дробь, знаменатель которой равен 10, 100, 1000 и вообще  , может быть записана в виде десятичной дроби.
, может быть записана в виде десятичной дроби.
Например,  Аналогично можно записывать неправильную дробь и смешанное число, например
Аналогично можно записывать неправильную дробь и смешанное число, например  По сути, десятичное число – просто удобная форма записи дроби с указанными знаменателями.
По сути, десятичное число – просто удобная форма записи дроби с указанными знаменателями.
Рассмотрим десятичную дробь 3,1415. Имеем:
 |
Таким образом, в десятичной дроби 3,1415 содержится 3 единицы, 1 десятая, 4 сотых, 1 тысячная, 5 десятитысячных. Вообще, в десятичной дроби может быть сколько угодно разрядов: десятые, сотые, тысячные, десятитысячные, стотысячные и т. д.
Рассмотренную дробь можно записать так:
 |
Но  а
а  Таким образом, десятичная дробь не изменится, если к ней справа приписать любое количество нулей.
Таким образом, десятичная дробь не изменится, если к ней справа приписать любое количество нулей.
Ясно, что верно и обратное: десятичная дробь не изменится, если отбросить нули, стоящие справа в конце неё. Например,  (нули, не стоящие в конце числа, отбрасывать нельзя).
(нули, не стоящие в конце числа, отбрасывать нельзя).
Перечислим, как с десятичными числами можно проводить известные нам арифметические операции.
Сложение и вычитание. Сложение и вычитание десятичных чисел производится точно так же, как сложение и вычитание целых чисел, нужно только записывать одноимённые разряды один под одним. Например,

Умножение. Умножение десятичных дробей проводится следующим образом. Перемножаем данные числа, как целые, не обращая внимания на запятые. Затем ставим в произведении запятую по следующему правилу: число знаков после запятой в произведении равно сумме чисел знаков после запятой во всех сомножителях. Заметим, что до постановки запятой отбрасывать знаки нельзя.
Деление. Для того чтобы разделить десятичную дробь (или целое число) на десятичное дробь, нужно отбросить запятую в делителе; в делимом же переносим запятую вправо на столько знаков, сколько их было в дробной части делителя (в случае необходимости в конце делимого приписывают нули). После чего делим полученное число на натуральное.
Разделить 9,43 : 0,23.
 Итак, 9,43 : 0,23 = 41.
Итак, 9,43 : 0,23 = 41.
Билет № 2. Вопрос 2.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства:
· Все свойства параллелограмма.
· Диагонали прямоугольника равны:  .
.
· Вокруг прямоугольника всегда можно описать окружность.

Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Квадрат – параллелограмм, у которого все стороны равны и все углы — прямые; или прямоугольник, у которого все стороны равны; или ромб, у которого все углы — прямые. 
Свойства:
· Все свойства прямоугольника и ромба.
Свойства ромба:
· Все свойства параллелограмма.
· Диагонали ромба взаимно перпендикулярны.
· Диагонали ромба являются биссектрисами углов.
Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3.Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
6.Биссектриса отсекает от параллелограмма равнобедренный треугольник
Билет № 3. Вопрос 1.
Если числа а отлично от нуля, а n- целое отрицательное число, то  и
и  , Число a называется основанием степени, число n − показателем степени.
, Число a называется основанием степени, число n − показателем степени.
Примеры. Вычислить:

Решение.

Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:

Примеры. Вычислить: 
Решение.

Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Свойства
· а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
· а1=а Любое число в первой степени равно самому себе.
· am∙an=am+n При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
· am:an=am— n При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
· (am)n=amn При возведении степени в степень основание оставляют прежним, а показатели перемножают
· (a∙b)n=an∙bn При возведении произведения в степень возводят в эту степень каждый из множителей.
· (a/b)n=an/bn При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.
Примеры Упростить:

Решение.

При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем:  и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .

В примере 9) представим 73 как 72∙7, а степень 45 как 43∙42, а затем сократим дробь на (72∙43).
 В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).
В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).
Билет № 3. Вопрос 2.
Ромб — параллелограмм, у которого все стороны равны.

Свойства:
· Все свойства параллелограмма.
· Диагонали ромба взаимно перпендикулярны.
· Диагонали ромба являются биссектрисами углов.
· В ромб всегда можно вписать окружность.
Признаки ромба:
· Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.
· Если в параллелограмме диагонали являются биссектрисами углов, то этот параллелограмм — ромб.
Свойства параллелограмма
· 1. Противоположные стороны параллелограмма попарно равны
· 2. Противоположные углы параллелограмма попарно равны
· 3.Сумма смежных (соседних) углов параллелограмма равна 180 градусов
· 4. Сумма всех углов равна 360°
· 5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
· 6.Биссектриса отсекает от параллелограмма равнобедренный треугольник
Билет № 4. Вопрос 1.
Уравнением называют равенство, содержащее переменную, значение которой нужно найти.
Значения неизвестных, при которых уравнение обращается в истинное равенство, называются решениями (корнями) уравнения. Решить уравнение – это значит найти все его корни или убедиться, что корней нет.
Линейное уравнение — такое, в котором присутствует лишь одна переменная, причём исключительно в первой степени.
Под простейшим уравнением подразумевается уравнение вида:
ax+b=0
Все остальные линейные уравнения сводятся к простейшим с помощью алгоритма:
1. Раскрыть скобки, если они есть;
2. Перенести слагаемые, содержащие переменную, в одну сторону от знака равенства, а слагаемые без переменной — в другую;
3. Привести подобные слагаемые слева и справа от знака равенства;
4. Разделить полученное уравнение на коэффициент при переменной x
Если a = b = 0, то решением уравнения ax + b = 0 является любое число.
Если a = 0 и b ≠ 0, то уравнение корней не имеет.
Если a ≠ 0, то уравнение ax + b = 0 называется линейным и имеет ровно одно решение 
Пример 1
Решите уравнение x = 1.
Решение
| Корнем этого уравнения является число 1, поскольку при подстановке вместо x этого числа получается верное числовое равенство. Ответ. 1. |
Пример 2
Решите уравнение 0 ∙ x + 1 = 0.
Решение
Имеем:  Это уравнение не имеет решений, поскольку ни при каких значениях переменной (которая, очевидно, явно не входит в уравнение) равенство 1 = 0 не имеет место. Ответ. Нет решений. Это уравнение не имеет решений, поскольку ни при каких значениях переменной (которая, очевидно, явно не входит в уравнение) равенство 1 = 0 не имеет место. Ответ. Нет решений. |
Пример 3
Решите уравнение 0 ∙ x + 1 = 1.
Решение
Имеем  Решением этого уравнения является любое действительное число. В самом деле, при любом значении переменной равенство 1 = 1 является верным. Ответ. x − любое число. Решением этого уравнения является любое действительное число. В самом деле, при любом значении переменной равенство 1 = 1 является верным. Ответ. x − любое число. |
Билет № 4. Вопрос 2.
У геометрической фигуры — треугольника 3стороны и 3 вершины. Треугольник получается, если три точки, которые не лежат на одной прямой, соединить отрезками.
Сторона треугольника — отрезок, соединяющий две его вершины.
Неравенство треугольника — в любом треугольнике сумма длин двух сторон больше длины третьей стороны:  ,
,  ,
,  .
.
Угол — часть плоскости, ограниченная двумя лучами, выходящими из вершины.
Теорема. Сумма углов треугольника равна  :
:  .
.
Следствие: В треугольнике не может быть более одного тупого или прямого угла.
 Внешний угол — угол, смежный с каким-нибудь углом треугольника.
Внешний угол — угол, смежный с каким-нибудь углом треугольника.
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Биссектриса угла — прямая, делящая угол на две равные части.
Биссектриса угла треугольника —отрезок биссектрисы угла, лежащий внутри треугольника.
Теорема. Если точка лежит на биссектрисе треугольника, то она равноудалена от сторон угла.
Верно и обратное утверждение: если точка равноудалена от сторон угла, то она лежит на биссектрисе угла этого треугольника.
Медиана — это отрезок, соединяющий какую-либо вершину треугольника с серединой противоположной стороны.
Высота — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
Высоты треугольника пересекаются в одной точке, медианы треугольника пересекаются в одной точке и биссектрисы треугольника пересекаются в одной точке.
 Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
Теорема. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине:  ,
,  .
.
Билет № 5. Вопрос 1.


 ВЫНЕСЕНИЕ МНОЖИТЕЛЯ ИЗ-ПОД ЗНАКА КОРНЯ
ВЫНЕСЕНИЕ МНОЖИТЕЛЯ ИЗ-ПОД ЗНАКА КОРНЯ
1) Представим подкоренное выражение в виде произведения таких множителей, чтобы из одного можно было бы извлечь квадратный корень.
2) Применим теорему о корне из произведения.
3) Извлечь корень
Пример.


Запишем данное преобразование и в буквенном виде:
Если а 
ВНЕСЕНИЕ МНОЖИТЕЛЯ ПОД ЗНАК КОРНЯ
1) Представим произведение в виде арифметического квадратного корня.
2) Преобразуем произведение квадратных корней в квадратный корень из произведения подкоренных выражений..
3) Выполним умножение под знаком корня.
Пример.

Запишем данное преобразование в буквенном виде:
Если 
При сравнении квадратных корней необходимо помнить, что чем больше число под знаком корня, тем больше сам корень.
Билет № 5. Вопрос 2.
Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.
Свойства площадей:
1. Равные многоугольники имеют равные площади.
2. Если многоугольник состоит из нескольких многоугольников (которые не перекрываются), то его площадь равна сумме площадей этих многоугольников.
3. Площадь квадрата равна квадрату его стороны.
Рассмотрим площади четырехугольников.
Площадь параллелограмма
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону.

Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
 Формулы площади квадрата
Формулы площади квадрата
Формулы площади трапеции
 Площадь трапеции равна произведению полусуммы ее оснований на высоту
Площадь трапеции равна произведению полусуммы ее оснований на высоту
| S = | (a + b) · h | |
где S - Площадь трапеции,
a, b - длины основ трапеции,
c, d - длины боковых сторон трапеции,
Билет № 6. Вопрос 1.

Корнем квадратного уравнения ax2+bx+c=0 называют всякое значение переменной x, при котором квадратный трехчлен ax2+bx+c обращается в нуль; такое значение переменной x называют также корнем квадратного трёхчлена.
Можно сказать и так: корень квадратного уравнения ax2+bx+c=0 — это такое значение x, подстановка которого в уравнение обращает уравнение в верное числовое равенство 0=0.
Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.
Алгоритм решения неполных квадратных уравнений.

Примеры

Билет № 6. Вопрос 2.
 Треугольник называется прямоугольным, если один из его углов - прямой.
Треугольник называется прямоугольным, если один из его углов - прямой.
 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2=a2+b2.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2=a2+b2.
Известны очень многие доказательства теоремы с разными математическими методами, но одни из самых наглядных связаны с площадями.
1. Построим квадрат, сторона которого равна сумме катетов данного треугольника a+b. Площадь квадрата равна 2  (a+b):
(a+b):
 2. Если провести гипотенузы c, очевидно, что они образовали квадрат внутри построенного квадрата.
2. Если провести гипотенузы c, очевидно, что они образовали квадрат внутри построенного квадрата.
 Стороны четырёхугольника равны c, а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают 90°, то угол четырёхугольника также равен 90°, потому что вместе все три угла дают 180°.
Стороны четырёхугольника равны c, а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают 90°, то угол четырёхугольника также равен 90°, потому что вместе все три угла дают 180°.
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников 4⋅  =2ab и площади квадрата c2, образованного гипотенузами: S=c2+2аb
=2ab и площади квадрата c2, образованного гипотенузами: S=c2+2аb
3. На двух сторонах квадрата поменяем местами отрезки a и b, при этом длина стороны квадрата не меняется.
Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами a и b a2+b2 и двух площадей прямоугольников аb + аb: S=a2+b2+2ab
4. Из этого следуют выводы: S=c2+2аb и S=a2+b2+2ab
Площадь четырех треугольников составляет и c2=a2+b2, что и является одним из доказательств теоремы Пифагора.
Обрати внимание!
Обратная теорема используется как признак прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Пример:
- Является ли треугольник со сторонами 6 см, 7 см и 9 см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
92=62+72;81≠36+49, значит, этот треугольник не прямоугольный.
- Является ли треугольник со сторонами 5 см, 12 см и 13 см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
132=122+52;169=144+25, значит, этот треугольник прямоугольный.
 Билет № 7. Вопрос 1.
Билет № 7. Вопрос 1.
Для построения графика функции  дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение
дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение  не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня.
не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня.
Итак, мы составили таблицу значений функции:
| x | 6,25 | ||||
| y | 2,5 |
Построим найденные точки (0; 0), (1;1), (4; 2), (6,25; 2,5), (0;3) на координатной плоскости. Они располагаются некоторой линии, начертим ее. Получили график функции  . Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции
. Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции  , ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
, ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
 Свойства функции
Свойства функции 
Описывая свойства этой функции, мы, как обычно, будем опираться на ее геометрическую модель — ветвь параболы (на рисунок).
1. Область определения функции — луч [0, +оо).
2. у = 0 при х = 0; поэтому начало координат принадлежит графику функции.
3. у > 0 при х > 0, график расположен в первой координатной четверти
4. Большему значению аргумента, соответствует большее значение функции, чем больше х, тем больше у.
5. Функция ограничена снизу, но не ограничена сверху. Т.к. вообще, какое бы положительное число ни взять, всегда найдется такое х, что будет выполняться неравенство  > m
> m
Функция  , ее свойства и график
, ее свойства и график
Коэффициент k может принимать любые значения, кроме k=0. Рассмотрим сначала случай, когда k=1; таким образом, сначала речь пойдёт о функции y= 
Чтобы построить график функции y=  , дадим независимой переменной x несколько конкретных значений и вычислим (по формулe y=
, дадим независимой переменной x несколько конкретных значений и вычислим (по формулe y=  ) соответствующие значения зависимой переменной y. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные.
) соответствующие значения зависимой переменной y. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные.
Первый этап. Если x=1, то y=1 (напомним, что мы пользуемся формулой y=  );
);


Второй этап. Рассмотрим отрицательные значения




1. Область определения функции состоит из всех чисел, кроме x=0.
2. y>0 при x>0; y<0 при x<0.
3. Функция убывает на промежутках (−∞;0) и (0;+∞);
4. Функция не ограничена ни снизу, ни сверху.
5. Функция непрерывна на промежутках (−∞;0) и (0;+∞) и претерпевает разрыв при x=0.
6. Область значений функции — объединение двух открытых лучей (−∞;0)∪(0;+∞).
1. Область определения функции состоит из всех чисел, кроме x=0.
2. y>0 при x<0; y<0 при x>0.
3. Функция возрастает на промежутках (−∞;0) и (0;+∞);
4. Функция не ограничена ни снизу, ни сверху.
5. Функция непрерывна на промежутках (−∞;0) и (0;+∞) и претерпевает разрыв при x=0.
6. Область значений функции — объединение двух открытых лучей (−∞;0)∪(0;+∞).
Билет № 7. Вопрос 2.

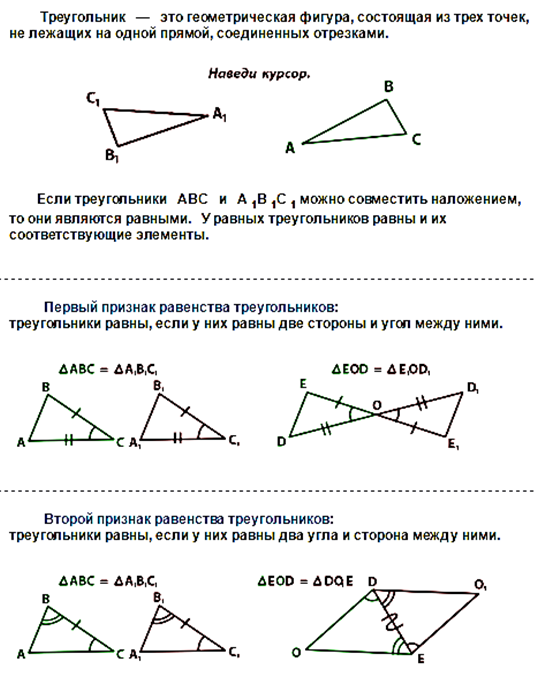
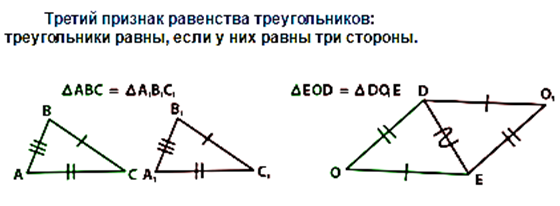
 Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
 Признаки подобия треугольников
Признаки подобия треугольников
Билет № 8. Вопрос 1.
Алгебраическое выражение − это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и скобок. Простейшим алгебраическим выражением является одночлен.
Одночленом называется выражение, которое содержит числа, натуральные степени переменных и их произведения, и при этом не содержит никаких других действий с этими числами и переменными. Например, 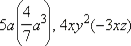 − одночлены, а выражения
− одночлены, а выражения 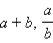 − не одночлены.
− не одночлены.
Одночлен называется представленным в стандартном виде, если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных. Числовой множитель у одночлена стандартного вида называется коэффициентом одночлена, сумму показателей степени переменных называют степенью одночлена. Ясно, что произведение одночленов также будет одночленом; ясно также, что одночлен в некоторой натуральной степени также является одночленом. Результаты таких действий (умножение одночленов и возведение одночлена в степень) обычно приводят к стандартному виду.
Пример 1
Привести к стандартному виду одночлены: 1) 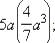 2)
2) 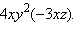
Решение 1)  2) 4xy2(–3xz) = –12x2y2z.
2) 4xy2(–3xz) = –12x2y2z.
Два одночлена, приведённых к стандартному виду, называются подобными, если они совпадают или же отличаются только числовым коэффициентом. Сложение и вычитание подобных одночленов называется приведением подобных слагаемых.
Многочленом называется сумма одночленов. Если все одночлены в многочлене приведены к стандартному виду, то говорят, что это многочлен стандартного вида. Алгебраическое выражение, не содержащее операции деления и извлечения корня (такое выражение называется целым), всегда может быть приведено к многочлену стандартного вида. Степенью многочлена называется наибольшая из степеней его слагаемых.
Пример 3
Привести к многочлену стандартного вида (a – b)(a + b).
Решение
| Имеем (a – b)(a + b) = (a – b) · a + (a – b) · b = a2 – ba + ba – b2 = a2 – b2. |
Пример 4
Привести к многочлену стандартного вида (a2 – ab) – (3ab – 2a2 – 5b(a + b2)).
Решение
| (a2 – ab) – (3ab – 2a2 – 5b(a + b2)) = a2 – ab – 3ab + 2a2 + 5ba + 5b3 = 3a2 + ab + 5b3. Часто бывает полезно преобразовать многочлен так, чтобы он был представлен в виде произведения нескольких сомножителей. Такое тождественное преобразование называется разложением многочлена на множители. 1. Вынесение множителя за скобку. Из распределительного закона непосредственно следует, что ac + bc = c(a + b). Этим можно воспользоваться для вынесения множителя за скобки. 2. Использование формул сокращённого умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения. a2 – b2 = (a + b)(a – b) , (a + b)2 = a2 + 2ab + b2, (a – b)2 = a2 – 2ab + b2, a3 + b3 = (a + b)(a2 – ab + b2), a3 – b3 = (a – b)(a2 + ab + b2), (a + b)3 = a3 + 3a2b + 3ab2 + b3, (a – b)3 = a3 – 3a2b + 3ab2 – b3 3. Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения. |
Билет № 8. Вопрос 2.
Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R . Центр окружности обозначают буквой O.
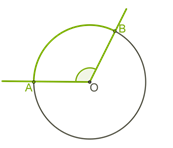 Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет окружность на две полуокружности и равен двум радиусам.
Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет окружность на две полуокружности и равен двум радиусам.

Билет № 9. Вопрос 1.





Билет № 9. Вопрос 2.
Билет № 10. Вопрос 1.
Дробное выражение - это математическое выражение, которое помимо действий сложения, вычитания и умножения, выполненных с числами и буквенными переменными, а также деления на число не равное нулю, содержит также деление на выражения с буквенными переменными.
Рациональные выражения - это все целые и дробные выражения. Рациональные уравнения - это уравнения, у которых левая и правые части являются рациональными выражениями. Если в рациональном уравнении левая и правая части будут являться целыми выражениями, то такое рациональное уравнение называется целым.
Если в рациональном уравнении левая или правая части будут являться дробными выражениями, то такое рациональное уравнение называется дробным.
Чтобы решить дробное уравнение, необходимо:
1. найти общий знаменатель дробей, входящих в уравнение;
2. умножить обе части уравнения на общий знаменатель;
3. решить получившееся целое уравнение;
4. исключить из его корней те, которые обращают в ноль общий знаменатель.
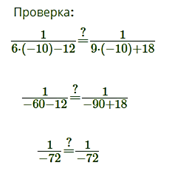


Билет № 10. Вопрос 2.
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается 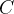 . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается
. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается 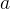 .
.
Угол 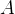 обозначается соответствующей греческой буквой
обозначается соответствующей греческой буквой 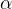 .
.
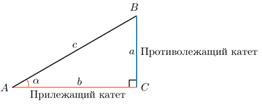
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет 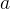 , лежащий напротив угла
, лежащий напротив угла 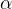 , называется противолежащим (по отношению к углу
, называется противолежащим (по отношению к углу 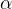 ). Другой катет
). Другой катет 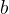 , который лежит на одной из сторон угла
, который лежит на одной из сторон угла 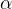 , называется прилежащим.
, называется прилежащим.
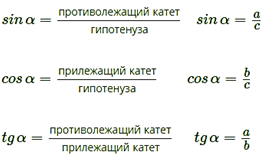
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
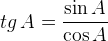
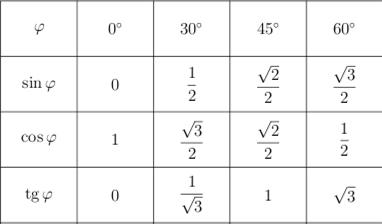
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

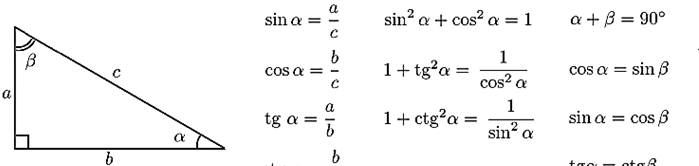
таблица значений синуса, косинуса, тангенса
Билет № 11. Вопрос 1.


Билет № 11. Вопрос 2.
 В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь
В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь
