Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.)

3. Сумма углов треугольника равна 180 ° (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60 °).

4. Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ.

5. Любая сторона треугольника меньше суммы двух других сторон и больше их разности:

• a < b + c,
• a > b – c;
• b < a + c,
• b > a – c;
• c < a + b,
• c > a – b.

Билет №17

1, Простые числа. Разложение числа на простые множители

Про­стым на­зы­ва­ют число, ко­то­рое имеет ровно два раз­лич­ных де­ли­те­ля.

Раз­ло­жить на­ту­раль­ное число на мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния на­ту­раль­ных чисел.

Раз­ло­жить на­ту­раль­ное число на про­стые мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния про­стых чисел.

Всякое составное число можно разложить на простые множители.

При любом способе получается одно и то же разложение,

если не учитывать порядка записи множителей.

Последовательность действий при разложении на простые множители:

1. Проверяем, не является ли предложенное число простым.

2. Если нет, то подбираем, руководствуясь признаками деления

делитель,

из простых чисел начиная с наименьшего (2, 3, 5 …).

3. Повторяем это действие до тех пор, пока частное не окажется

простым числом.

Разложим на простые множители число 27 :

27 не является простым.

27 на 2 не делится.

27 делится на 3, получаем 27 : 3 = 9 .

9 на 2 не делится.

9 делится на 3, 9 : 3 = 3.

3 простое число.

Результат: 27 = 3 • 3 • 3.

27 3

9 3

3 3

Разложим на простые множители число 378 :

378 2

189 3

63 3

21 3

7 7

378 не является простым.

378 делится на 2,

так как оканчивается на четное число ( 8 ).

378 : 2 = 189 .

189 делится на 3,

потому что сумма его цифр делится на 3,

получаем 189 : 3 = 63 .

63 так же делится на 3, получаем 63 : 3 = 21 .

21 так же делится на 3, получаем 21 : 3 =7

7 простое число.

Вертикальные углы

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

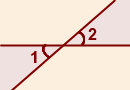∠1 и ∠2 — вертикальные углы

При пересечении двух прямых образуется две пары вертикальных углов:

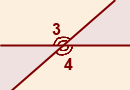∠3 и ∠4 — вертикальные углы

Свойство вертикальных углов.

Вертикальные углы равны. При пересечении двух прямых образуется две пары равных межу собой углов.

Билет №18

1. Наибольший делитель.

Наибольший общий делитель (НОД) двух и более чисел — это
самое большее натуральное число, на которое эти числа делятся
без остатка.

Например:

у чисел 12 и 8 наибольший общий делитель (НОД) равен 4,

а у чисел 20 и 35 (НОД) равен 5

Если у нескольких чисел нет общих делителей кроме единицы, то эти
числа называются взаимно простыми.

Например:

у чисел 5 и 8 , 11 и 18 , 16 и 27 (НОД) равен 1 .

Для нахождения наибольшего общего делителя двух или более чисел,
например 36 и 24 , надо:

1) разложить их на простые множители;

36 = 2 • 2 • 3 • 3 ; 24 = 2 • 2 • 2 • 3 .

2) в группах множителей ( 2 • 2 • 3 • 3 ) и ( 2 • 2 • 2 • 3 ) , входящих в
разложение этих чисел, оставляем только совпадающие множители;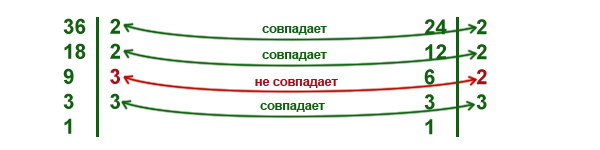

( 2 • 2 • 3 ) и ( 2 • 2 • 3 )

3) найти произведение оставшихся множителей. 2 • 2 • 3 = 12

Наибольший общий делитель чисел 36 и 24 равен 12 .

Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.

Например: у чисел 12 , 36 и 48 НОД = 12 .

1. Площадь треугольника

Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.

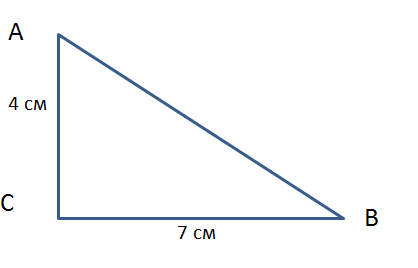
В нашем примере стороны равны 7 см и 4 см. Формула для расчета площади треугольника записывается так:
S _{прямоугольного треугольника АВС} = ВС * СА : 2

Подставим в формулу наши данные и получим:
S _{прямоугольного треугольника АВС} = 7 см * 4 см : 2 = 14 см²

Теперь рассмотрим произвольный треугольник.

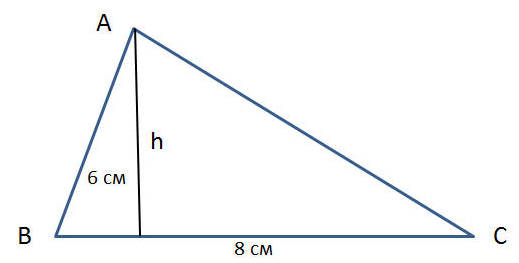
Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см. Как и в предыдущем примере, рассчитываем площадь по формуле:
S _{произвольного треугольника АВС} = ВС * h : 2.

Подставим в формулу наши данные и получим:
S _{произвольного треугольника АВС} = 8 см * 6 см : 2 = 24 см².

Билет №19

1. Наименьшее общее кратное

Наименьшим общим кратным натуральных чисел a и b называют
наименьшее натуральное число, которое кратно и a , и b .

Чтобы найти наименьшее общее кратное нескольких натуральных
чисел, например 6 и 8 , надо:

1) разложить их на простые множители;

6 = 2 • 3 ;

8 = • 2 • 2 ;

2 есть в разложении числа 6 ( вычеркиваем ее );

2) выписать множители, входящие в разложение одного из чисел;

2 • 3 ;

3) домножить их на недостающие множители из разложений
остальных чисел;

2 • 3 • 2 • 2 ;

4) найти произведение получившихся множителей.

2 • 3 • 2 • 2 = 24;

НОК ( 6 и 8 ) = 24 .

Найдем наименьшее общее кратное чисел 24 и 36:

1) разложим их на простые множители;

24 = 2 • 2 • 2 • 3 ;

36 = • 3 ;

2 , 2 и 3 есть в разложении числа 24 ( вычеркиваем их );

2) выпишем множители, входящие в разложение числа 24 ;

2 • 2 • 2 • 3 ;

3) домножим их на недостающий множитель из разложения числа 36 ;

2 • 2 • 2 • 3 • 3 ;

4) найти произведение получившихся множителей.

2 • 2 • 2 • 3 • 3 = 72;

НОК ( 24 и 36 ) = 72 .

Найдем наименьшее общее кратное чисел 30 и 42: 1) разложим их на простые множители; 30 = 2 • 3 • 5 ; 42 = • 7 ; 2 и 3 есть в разложении числа 30 ( вычеркиваем их ); 2) выпишем множители, входящие в разложение числа 30 ; 2 • 3 • 5 ; 3) домножим их на недостающий множитель из разложения числа 42 ; 2 • 3 • 5 • 7 ; 4) найти произведение получившихся множителей. 2 • 3 • 5 • 7 = 210; НОК ( 30 и 42 ) = 210 .

Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел. Например: у чисел 12 , 6 и 4 НОК = 12 .

1. Диаграммы

Диаграммы являются графическим изображением данных (цифры, факты и пр.) с целью их наглядного представления. Диаграмма – чертеж, на котором статистические данные изображаются с помощью геометрических фигур или рисунков.

Основная задача при работе с диаграммой – сопоставление, сравнение числовых величин, выработка умения объяснить полученные соотношения, делать выводы. Выбор типа диаграммы зависит от тех задач, для решения которых она предназначена. Диаграмма должна быть достаточно простой и наглядной.

Билет №20

1. Признаки делимости натуральных чисел

Для упрощения деления натуральных чисел были выведены правила деления на числа первого десятка и числа 11, 25, которые объединены в раздел признаков делимости натуральных чисел.

Натуральные числа, имеющие в первом разряде цифры (оканчивающиеся на) 2,4,6,8,0, называются четными.

На 2 делятся все четные натуральные числа, например: 172, 94,67 838, 1670.

На 3 делятся все натуральные числа, сумма цифр которых кратна 3. Например:
39 (3 + 9 = 12; 12 : 3 = 4);

16 734 (1 + 6 + 7 + 3 + 4 = 21; 21:3 = 7).

На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4. Например:
124 (24 : 4 = 6);
103 456 (56 : 4 = 14).

На 5 делятся все натуральные числа, оканчивающиеся на 5 или 0. Например: 125; 10 720.

На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно (все четные числа, которые делятся на 3). Например: 126 (б — четное, 1 + 2 + 6 = 9, 9 : 3 = 3).

На 9 делятся те натуральные числа, сумма цифр которых кратна 9. Например:
1179 (1 + 1 + 7 + 9 = 18, 18 : 9 = 2).

На 10 делятся все натуральные числа, оканчивающиеся на 0. Например: 30; 980; 1 200; 1 570.

На 11 делятся только те натуральные числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11. Например:
105787 (1 + 5 + 8 = 14 и 0 + 7 + 7 = 14);
9 163 627 (9 + 6 + б + 7 = 28 и 1 + 3 + 2 = 6);
28 — 6 = 22; 22 : 11 = 2).

На 25 делятся те натуральные числа, две последние цифры которых — нули или составляют число, кратное 25. Например:
2 300; 650 ( 50 : 25 = 2);

1 475 (75 : 25 = 3).

На разрядную единицу делятся те натуральные числа, у которых количество нулей больше или равно количеству нулей разрядной единицы. Например: 12 000 делится на 10, 100 и 1000.

1. Свойства углов треугольника

Треугольник — фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.
Точки называют вершинами треугольника, а отрезки — сторонами треугольника.

Сумма углов треугольника равна 180​∘​​.

У любого треугольника хотя бы два угла острые.

Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.