Для касательной и секущей к окружности, проведённых из одной точки, квадрат расстояния от этой точки до точки касания равен произведению длины секущей на длину её внешней части.

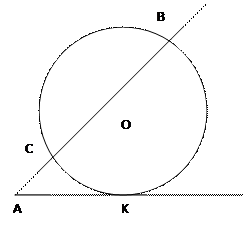Дано: . (O;R), AK — касательная, AB — секущая, (O;R)∩AK=K, (O;R)∩AB=B, C

Доказать: АК²=АВ*АС

Доказательство: Проведём хорды BK и CK.

Рассмотрим треугольники ABK и AKC.

У них ∠A — общий.

∟АКС=1/2UСК (как угол между хордой и касательной)

∟АВК=1/2UСК (как вписанный угол, опирающийся на дугу CK). Следовательно, ∠ABK=∠AKC. Значит, треугольники ABK и AKC подобны (по двум углам).

Из подобия треугольников следует пропорциональность их соответствующих сторон:

АВ/АК=АК/АС По основному свойству пропорции:

АК²=АВ*АС ч.т.д.

№ 6.2 (из учебника Л.С. Атанасяна №659)

Градусные меры дуг окружности, заключённых между параллельными хордами, равны.

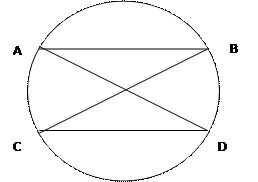
Дано: АВ и СD – хорды, АВ‖СD

Доказать: дуга АС = дуге ВD

Доказательство: ∟ВСD=∟ACD (как накрест лежащий, при АВ ‖ǁ СDи АD–секущей); ∟ВСDи ∟ADC–вписанные углы, значит, ∟ВСD=1/2 дуги ВD=∟ADC=1/2 дуги АС → дуга ВD = дуге АС ч.т.д.

№ 6.3 (из учебника Л.С. Атанасяна №696

Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.

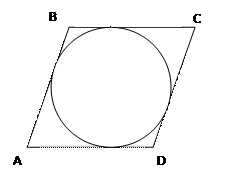Дано: АВСD –парал-мм., (О;r) – вписанная окружность

Доказать: АВСD – ромб

Доказательство: т.к. окружность вписанная, то ВС+АD=AB+CDили 2ВС=2АВ, ВС=АВ=СD=AD → ABCD–ромб ч.т.д.

№ 6.4 (из учебника Л.С. Атанасяна №710)

Если около трапеции можно описать окружность, то эта трапеция равнобедренная.

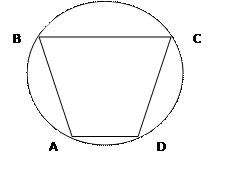Дано: АВСD – трапеция, (О;R) – описанная окружность

Доказать: АВСD – равнобедренная трапеция

Доказательство: т.к. окружность описанная, то ∟А+∟С=180 ͦ и ∟В+∟D=180 ͦ; ∟А+∟В=180 ͦ и ∟С+∟D=180 ͦ(как односторонние), значит, ∟А+∟С=180 ͦ=∟А+∟В → ∟В=∟С и ∟В+∟D=180 ͦ=∟B+∟A→∟A=∟D.

Значит, углы при основании равны → АВСD–равнобедренная трапеция ч.т.д.

№ 6.5 (из учебника Л.С. Атанасяна №719)

Через точку, лежащую вне окружности, проведены 2 секущие. Угол между ними измеряется полуразностью дуг, заключённых внутри угла.

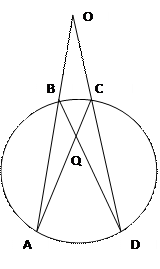Дано: (O;R) – окружность, точка О ɇ (О;R), ОА и ОD– секущие

Доказать: ∟АОD=1/2(дуга АD ─ дуга ВС)

Доказательство: Рассмотрим ∆АОС: ∟О=180 ͦ─∟А─∟С

∟С=180 ͦ─∟АСD; ∟АСD – вписанный, значит, ∟АСD=1/2дугиАD; ∟А – вписанный → ∟А=1/2 дуги ВС

∟АОD=180 ͦ─1/2дуги ВС─180 ͦ+1/2 дуги АD=1/2(дуга АD─ дуга ВС) ч.т.д.

№ 6.6 (из учебника Л.С. Атанасяна №892)

Площадь прямоугольной трапеции, описанной около окружности, равна произведению её оснований.

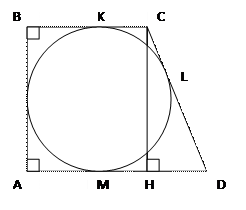Дано: (О;r) – вписанная окружность, АВСD–прямоугольная трапеция

Доказать: SABCD=BC*AD

Доказательство: проведём высоту СН. Рассмотрим ∆СНDв нём: СН=2r=d, НD=AD─BC, (ВС=r+(BC─r), (ВС─r)=KC, КС=СL (как отрезки касательных), значит, СL=BC─r; AD=r+(AD─r) (AD─r)=MD, МD=LD (как отрезки касательных) → LD=AD─r). Имеем: СD=(BC─r)+(AD─r)=BC+AD─2r.

Значит, по Т.Пифагора: (ВС+AD─2r)²=4r²+AD²─2BC*AD+BC²

Выразим rи получим, что r=BC*AD/BC+AD

SABCD=1/2СН*(BC+AD)=1/2*2r(BC+AD)=BC*AD* *(BC+AD)/BC+AD=BC*AD ч.т.д.

№ 6.7 (из учебника Л.С. Атанасяна №893)

В любом четырёхугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон.

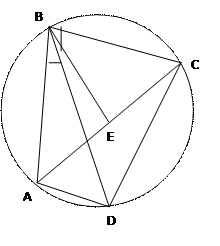Дано:АВСD – четырёхугольник, (О;R) – описанная окружность, BDи АС – диагонали

Доказать: BD*AC=BC*AD+AB*DC

Доказательство: Отметим точку Е такую, что ∟АВD=∟CBE. ∟ADB=∟BCE, т.к. они вписанные и опираются на одну дугу → ∆ABD~∆CBE по 2 углам, значит, ВС/ЕС=ВD/ADили BC*AD=EC*BD.

Рассмотрим ∆АВЕ и ∆BDC в них: ∟ВАС=∟BDC, т.к. они вписанные и опираются на одну дугу, ∟АВЕ=∟DBC, т.к. ∟ABD=∟EBC→∆ABE~∆BDC, значит, АВ/АЕ=ВD/СD или АВ*CD=AE*BD.

Имеем: ВС*АD+AB*CD=AE*BD+EC*BD; ВС*AD+AB*CD=(AE+EC)*BD; AE+EC=AC

BC*AD+AB*CD=BD*AC ч.т.д.

Подобие

№ 7.1 (из учебника Л.С. Атанасяна №267)

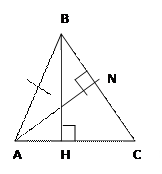Два остроугольных треугольника равны, если сторона и высоты, проведённые из концов этой стороны, одного треугольника соответственно равны стороне и высотам, проведённым из концов этой стороны, другого треугольника.

Дано: АВ=А₁В₁, ВН=В₁Н₁, АN=A₁N₁; AN, BH, B₁H₁ и А₁N₁ - высоты

Доказать: ∆АВС=∆А₁В₁С₁

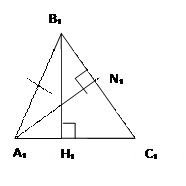Доказательство: рассмотрим ∆АВН и ∆А₁В₁Н₁ в них: АВ=А₁В₁ и ВН=В₁Н₁ (по условию), а также ∆ прямоугольные, значит, они равны по гипотенузе и катету → ∟А=∟А₁.

Рассмотрим ∆АВN и ∆А₁В₁N₁ в них: А₁N₁=ANAB=A₁B₁ (по условию) и ∆ прямоугольные, значит, они равны по гипотенузе и катету → ∟В=∟В₁. Имеем: АВ=А₁В₁, ∟А=∟А₁ и ∟В=∟В₁ → ∆АВС=∆А₁В₁С₁ по II ПРТ ч.т.д.

№ 7.2 (из учебника Л.С. Атанасяна№547)

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

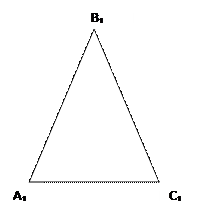Дано: ∆АВС~∆А₁В₁С₁

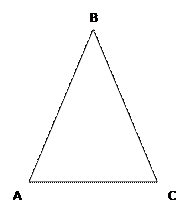Доказать: P∆ABC/P∆А₁В₁С₁=k

Доказательство: P∆ABC/P∆А₁В₁С₁=АВ+ВС+АС/А₁В₁+В₁С₁+А₁С₁

АВ/А₁В₁=k; АВ=А₁В₁k; ВС и АС (аналогично).

Значит, P∆ABC/P∆А₁В₁С₁=А₁В₁*k+В₁С₁*k+А₁С₁*k/А₁В₁+В₁С₁+А₁С₁=

=k(A₁B₁+B₁C₁+A₁C₁)/А₁В₁+В₁С₁+А₁С₁=k ч.т.д.