Тень, падающая от одной фигуры на другую

.

7.3. Тень, падающая от одной фигуры на другую

Метод обратных лучей

Метод обратных лучей успешно применяется при построении теней, падающих от одной геометрической фигуры на другую, и характеризуется следующими построениями:

а) строятся тени, падающие от обеих заданных фигур на какую-либо плоскость;

б) выявляются точки пересечения теней от двух линий, из которых одна принадлежит контуру первой фигуры, а другая — контуру второй;

в) при помощи обратных лучей (то есть лучей, параллельных лучам света, но имеющих обратное направление) “возвращаются” эти точки в пространство (на соответствующие контурные линии фигур);

г) с помощью полученных точек определяется искомая тень, падающая от одной фигуры на другую.

ПРИМЕР.

На рис. 86 показано применение метода обратных лучей на

примере построения падающей тени от прямой на плоскость треугольника.

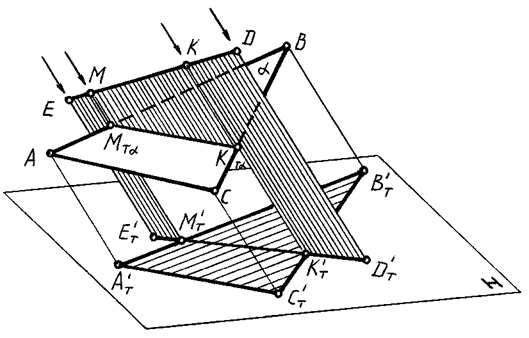
Рис. 86

Построены падающие тени от треугольника АВС и от прямой ED на плоскость Н. Через точки М_T' и М_T', общие теням прямой ED и сторонам АВ и ВС, проведены обратные лучи, пересекающие указанные прямые соответственно в точках М', М'', К' и K''. Точки М' и K' представляют собой тени от точек M'' и K'' прямой ЕD на стороны АВ и ВС. Искомая же тень будет определена точками M'K'.

На рис. 87 приведено решение этой задачи в ортогональных проекциях.

.

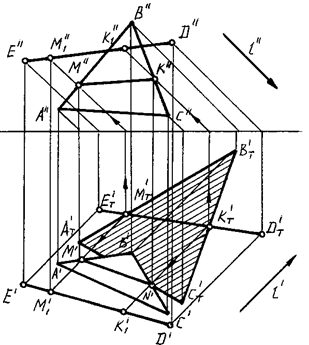
Рис. 87

2. Метод следа светового луча
(метод сечения лучевой плоскостью)

Метод следа луча основан на том, что тень, падающая от точки, есть след проведенного через нее луча.

На рисунке 88 приведено решение задачи на построение тени от прямой АВ на плоскость Q (CDEF) в ортогональных проекциях методом следа луча (или сечения лучевой плоскости).

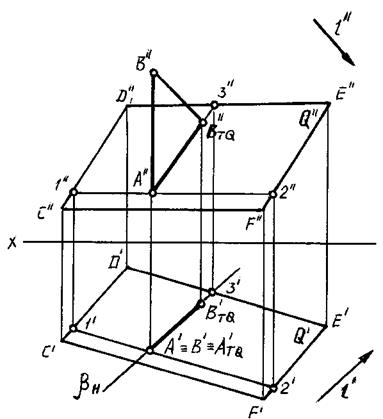
Рис. 88

В данном случае тень от прямой АВ на плоскость Q построена с помощью двух точек А_TQ(А_TQ',А_TQ'') и В_TQ(В_TQ',В_TQ''), в которых пересекаются с плоскостью Q(CDEF) соответственно данная прямая и световой луч, проходящий через точку В.

Плоскость b ^ H является лучевой плоскостью, которая проводится через луч ВВ_TQ для определения точки В_TQ(В_TQ',В_TQ'').

Тени геометрических тел

Выше говорилось, что тени делятся на собственные и падающие. Определение собственной тени сводится к нахождению ее контуров, то есть линий, отделяющих освещенную часть поверхности от неосвещенной.

Контур падающей тени можно рассматривать как тень, падающую от контура собственной тени.

Тени многогранников

На рисунке 89, 90 построены собственная и падающая тени прямой пятиугольной призмы.

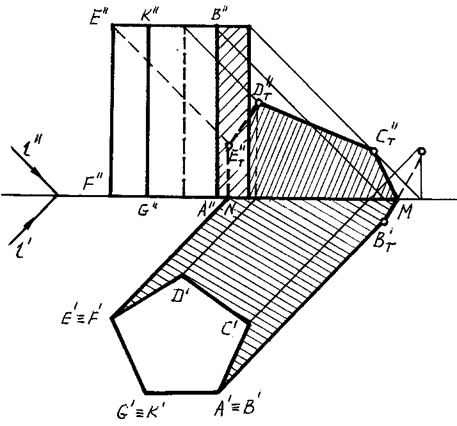
Рис. 89

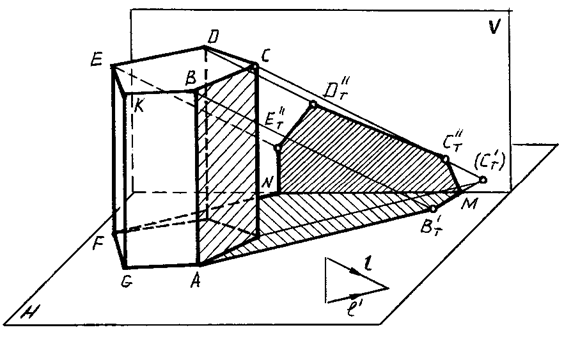
Рис. 90

Для определения контура собственной тени призмы необходимо установить освещенность ее граней. Так как боковые грани призмы перпендикулярны к плоскости Н, то их освещенность легко определить на горизонтальной проекции, где видно, что обращены к свету две грани: EFGK и KGAB.

Освещено также верхнее основание призмы.

Таким образом, контуром собственной тени является ломаная ABCDEFGA, от которой построена тень, падающая на плоскости H и V по правилам, изложенным в предыдущей теме.

На рисунке 91,92 приведен пример построения собственной и падающей теней правильной пятиугольной пирамиды SABCDE.

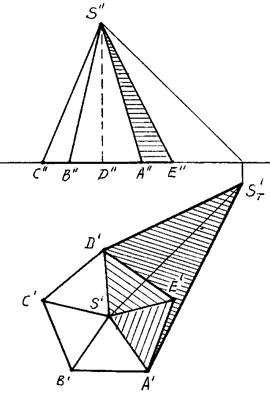
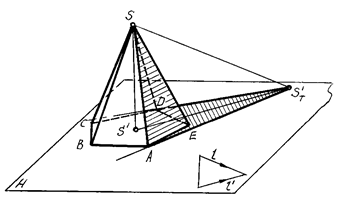
Рис. 91 Рис. 92

В отличие от прямой призмы, боковые грани пирамиды не являются горизонтально-проецирующими плоскостями, поэтому определить их освещенность непосредственно по горизонтальной проекции не всегда возможно.

Строим падающую тень S_T' от вершины S на плоскость Н и определяем падающие тени от боковых ребер пирамиды. Линиями контура падающей тени пирамиды оказались прямые S_T'А и S_T'D. Следовательно, контур собственной тени пройдет вдоль ребер SA и SD. Таким образом, в собственной тени будут находиться грани SAE, SDE и основание пирамиды.

Тени цилиндра

Чтобы построить контур собственной тени цилиндрической поверхности, необходимо провести к этой поверхности касательные лучевые плоскости, параллельные направлению лучей света, и найти линии касания (образующие цилиндра). Вдоль этих образующих пройдет контур собственной тени.

На рисунке 93 приведен пример построения собственной и падающей теней вертикально расположенного прямого кругового цилиндра. Контур собственной тени цилиндра проходит вдоль образующих АВ и CD и замыкается сверху полуокружностью АМС верхнего основания, а снизу — полуокружностью BND нижнего основания.

Контур падающей тени от цилиндра состоит из падающих теней от образующих АВ и СD и падающих теней от полуокружностей АМС и BND.

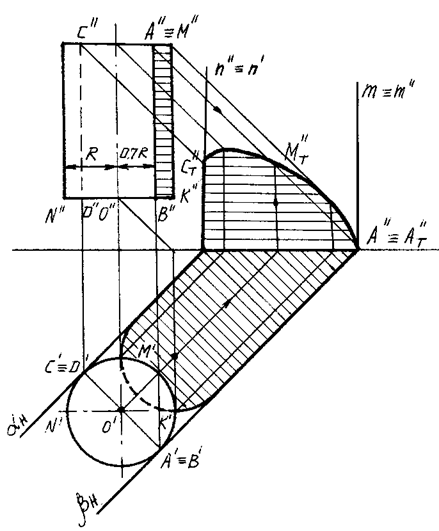
Рис. 93

Падающие тени от образующих АВ и СD определяются с помощью следов a_H, m, b_H и n, касательных лучевых плоскостей a и b. Тени, падающие от полуокружностей АМС и BND, определяются как в примерах предыдущей темы (рис. 85).

Собственную тень на вертикальном круговом цилиндре в ортогональных проекциях можно построить, не имея горизонтальной проекции цилиндра, так как известно, что расстояние от фронтальных проекций образующих АВ и CD до фронтальной проекции оси цилиндра равно радиусу цилиндр, умноженному на косинус 45^о, то есть:

O'B' = O'D' = 0,707 O''K'' (рис. 93).

Графическим путем проекции В'' и D'' точек B и D можно найти следующим образом (рис. 93): из точек O'' и K'' проводим под углом 45 градусов к отрезку O''K'' прямые — катеты прямоугольного треугольника O''1 K''. Из точки O'' радиусом O''1 проводим полуокружность, пересекающую прямую N''K'' в искомых точках B'' и D''.

Тени конуса

На рис. 94, 95 выполнены построения собственной и падающей теней конуса.

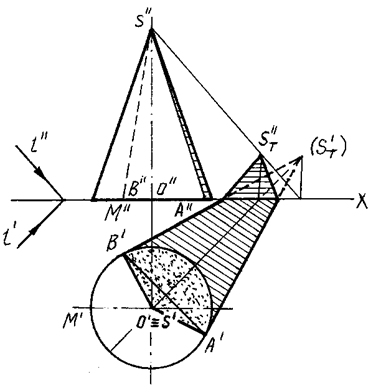
Рис. 94

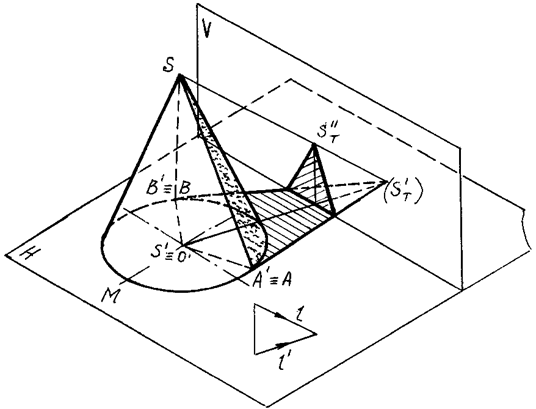
Рис. 95

Вначале определяется тень S_T' (мнимая), падающая от вершины S конуса на плоскость его основания Н; из полученной точки проводятся прямые, касательные к основанию конуса, и определяются точки касания А и В. Через эти точки проводятся образующие SA и SB, которые вместе с дугой основания АМВ образуют контур собственной тени.

Касательные S_T'A' и S_T'B' к основанию на рис. 94, 95 являются линиями контура падающей тени конуса. Однако, это справедливо лишь в том случае, если конус стоит на плоскости, на которую падает тень. На рисунке падающая тень имеет точки изломов на оси ОХ.

7.4. Тени геометрических тел

Выше говорилось, что тени делятся на собственные и падающие. Определение собственной тени сводится к нахождению ее контуров, то есть линий, отделяющих освещенную часть поверхности от неосвещенной.

Контур падающей тени можно рассматривать как тень, падающую от контура собственной тени.

Тени многогранников

На рисунке 89, 90 построены собственная и падающая тени прямой пятиугольной призмы.

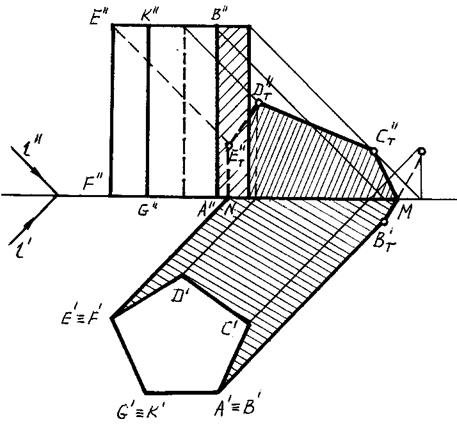
Рис. 89

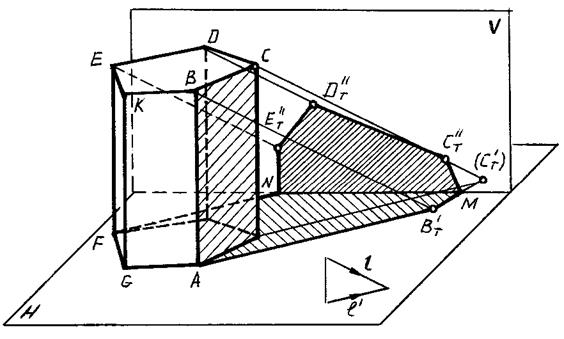
Рис. 90

Для определения контура собственной тени призмы необходимо установить освещенность ее граней. Так как боковые грани призмы перпендикулярны к плоскости Н, то их освещенность легко определить на горизонтальной проекции, где видно, что обращены к свету две грани: EFGK и KGAB.

Освещено также верхнее основание призмы.

Таким образом, контуром собственной тени является ломаная ABCDEFGA, от которой построена тень, падающая на плоскости H и V по правилам, изложенным в предыдущей теме.

На рисунке 91,92 приведен пример построения собственной и падающей теней правильной пятиугольной пирамиды SABCDE.

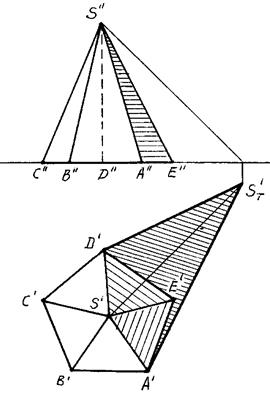
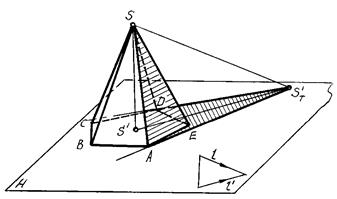
Рис. 91 Рис. 92

В отличие от прямой призмы, боковые грани пирамиды не являются горизонтально-проецирующими плоскостями, поэтому определить их освещенность непосредственно по горизонтальной проекции не всегда возможно.

Строим падающую тень S_T' от вершины S на плоскость Н и определяем падающие тени от боковых ребер пирамиды. Линиями контура падающей тени пирамиды оказались прямые S_T'А и S_T'D. Следовательно, контур собственной тени пройдет вдоль ребер SA и SD. Таким образом, в собственной тени будут находиться грани SAE, SDE и основание пирамиды.

Тени цилиндра

Чтобы построить контур собственной тени цилиндрической поверхности, необходимо провести к этой поверхности касательные лучевые плоскости, параллельные направлению лучей света, и найти линии касания (образующие цилиндра). Вдоль этих образующих пройдет контур собственной тени.

На рисунке 93 приведен пример построения собственной и падающей теней вертикально расположенного прямого кругового цилиндра. Контур собственной тени цилиндра проходит вдоль образующих АВ и CD и замыкается сверху полуокружностью АМС верхнего основания, а снизу — полуокружностью BND нижнего основания.

Контур падающей тени от цилиндра состоит из падающих теней от образующих АВ и СD и падающих теней от полуокружностей АМС и BND.

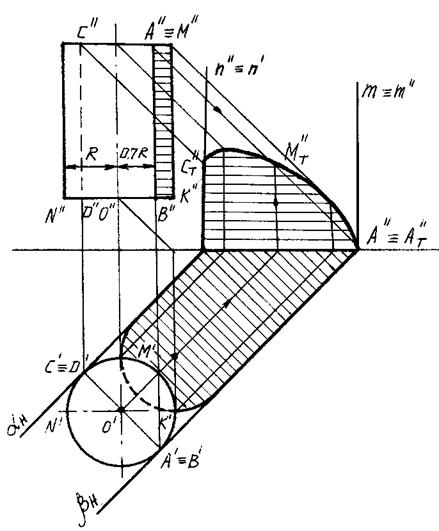
Рис. 93

Падающие тени от образующих АВ и СD определяются с помощью следов a_H, m, b_H и n, касательных лучевых плоскостей a и b. Тени, падающие от полуокружностей АМС и BND, определяются как в примерах предыдущей темы (рис. 85).

Собственную тень на вертикальном круговом цилиндре в ортогональных проекциях можно построить, не имея горизонтальной проекции цилиндра, так как известно, что расстояние от фронтальных проекций образующих АВ и CD до фронтальной проекции оси цилиндра равно радиусу цилиндр, умноженному на косинус 45^о, то есть:

O'B' = O'D' = 0,707 O''K'' (рис. 93).

Графическим путем проекции В'' и D'' точек B и D можно найти следующим образом (рис. 93): из точек O'' и K'' проводим под углом 45 градусов к отрезку O''K'' прямые — катеты прямоугольного треугольника O''1 K''. Из точки O'' радиусом O''1 проводим полуокружность, пересекающую прямую N''K'' в искомых точках B'' и D''.

Тени конуса

На рис. 94, 95 выполнены построения собственной и падающей теней конуса.

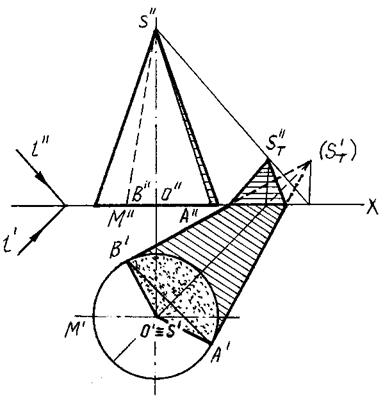
Рис. 94

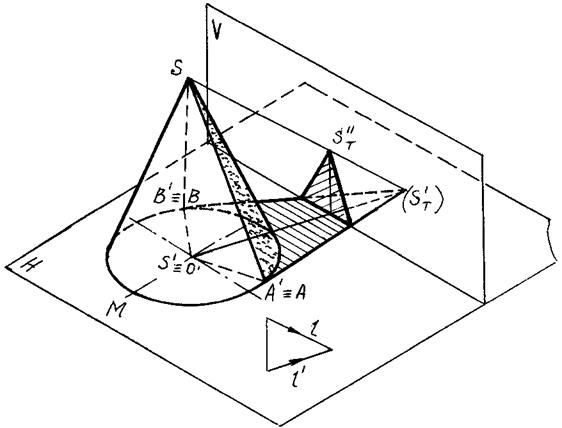
Рис. 95

Вначале определяется тень S_T' (мнимая), падающая от вершины S конуса на плоскость его основания Н; из полученной точки проводятся прямые, касательные к основанию конуса, и определяются точки касания А и В. Через эти точки проводятся образующие SA и SB, которые вместе с дугой основания АМВ образуют контур собственной тени.

Касательные S_T'A' и S_T'B' к основанию на рис. 94, 95 являются линиями контура падающей тени конуса. Однако, это справедливо лишь в том случае, если конус стоит на плоскости, на которую падает тень. На рисунке падающая тень имеет точки изломов на оси ОХ.