Прямоугольная диметрическая проекция

В прямоугольной диметрической проекции аксонометрические оси O^ox^o и O^oz^o составляют между собой угол 97^о10’. Ось O^oy^o является биссектрисой оставшегося угла, составляя с двумя другими осями равные углы 131^о25’ (рис. 11). При построении этой проекции принимают, что

K_x = K_z и K_y = 0,5K_x.

Тогда по основной теореме аксонометрии получаем из формулы

K²_x + K²_y + K²_z = 2, что 2K²_x + (0,5K_x)² = 2,

тогда K²_x = 8/9; K_x = 0,94.

Приведенные коэффициенты искажения будут равны:

K_x = K_z = 1; K_y = 0,5,

что соответствует увеличению изображения в 1,06 раза (1/0,94 = 1,06).

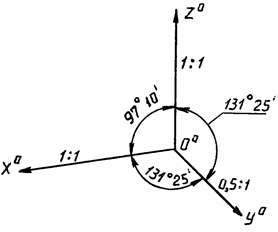
Рис. 11

Прямоугольная диметрия рекомендуется к применению в случае, когда наибольшее число характерных особенностей сосредоточено на одной стороне предмета. Наиболее отличающаяся особенностями сторона предмета располагается параллельно плоскости X^oO^oZ^o.

Косоугольная фронтальная диметрическая проекция

Аксонометрическая плоскость a располагается параллельно фронтальной плоскости проекций V (рис. 12). Поэтому аксонометрические оси O^ox^o и O^oz^o параллельны декартовым осям Ox и Oz. Соответственно, коэффициенты искажения K_x = K_z. Значение K_y принимается равным 0,5. Расположение аксонометрических осей показано на рисунке .

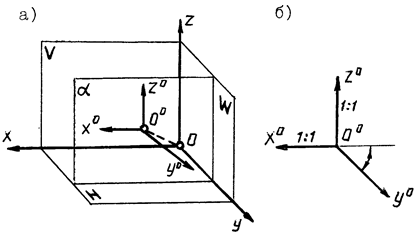
Рис. 12

Косоугольная фронтальная диметрия удобна в тех случаях, когда изображаемая геометрическая фигура содержит большое число окружностей (или других кривых, состоящих из дуг окружностей), лежащих на взаимно параллельных плоскостях. При расположении этих плоскостей параллельно аксонометрической плоскости, все окружности будут проецироваться на ней также в виде окружностей, что упрощает построение.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ И ПРЯМОЙ

План:

3.1. Комплексный чертеж точки

3.2. Проекции прямых общего положения

3.3. Проекции прямых уровня

Горизонталь - прямая равных высот

Фронталь - прямая равных глубин

Профильная прямая - прямая равных широт

3.4. Проекции проецирующих прямых

Горизонтально-проецирующая прямая

Фронтально-проецирующая прямая

Профильно-проецирующая прямая

3.5. Определение натуральной величины отрезка прямой общего положения

3.6. Деление отрезка прямой в данном отношениè

Комплексный чертеж точки

Внутри трехгранного угла, образованного горизонтальной (H), фронтальной (V) и профильной (W) плоскостями проекций, расположим какую-либо точку А (рис. 13).

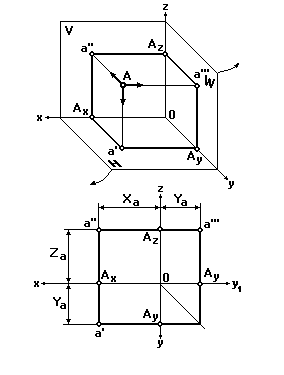
Рис. 13

Направим проецирующий луч перпендикулярно плоскости V. Точка пересечения этого луча с плоскостью V будет фронтальной проекцией a'' точки A. Спроецируем точку А на плоскость H и получим ее горизонтальную проекцию a'. Проецируя точку А на плоскость W, получим ее профильную проекцию a'''.

Для получения чертежа необходимо все три плоскости V, H и W вместе с построенными на них проекциями совместить в одну плоскость, т.е. развернуть их.

При этом плоскость H поворачивается вокруг оси x на 90 градусов книзу, плоскость W — вокруг оси z на 90 градусов вправо, а плоскость V остается неподвижной (при этом ось y как бы раздваивается).

В результате совмещения получают чертеж точки в трех проекциях. Очертания плоскостей H, V и W на чертеже не показывают.

Линию, связывающую горизонтальную и профильную проекции точки А, представляют двумя отрезками ломаной линии. Вершина ее лежит на биссектрисе угла, образованного осями y и y₁. Эту биссектрису называют постоянной линией чертежа.

Прямые линии, соединяющие проекции точки и перпендикулярные осям проекций, называют линиями проекционной связи (рис. ).

Координатный отрезок, равный превышению точки А над плоскостью H, называют высотой Za (аппликатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости V, называют глубиной Ya (ординатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости W, называют широтой Xa (абсциссой) точки А.

Горизонтальная проекция точки А определяется на эпюре ее координатами Xa и Ya, а фронтальная — координатами Xa и Za (рис. 13).