Введение. Предмет и метод начертательной геометрии
Начертательная геометрия — теоретическая база для составления чертежей.
“Паук совершает операции, напоминающие операции ткача, и пчела постройкой своих восковых ячеек посрамляет некоторых людей-архитекторов. Но и самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что прежде чем строить ячейку из воска, он уже состроил ее в своей голове”(К.Маркс, “Капитал”, т.1, с.189).
Задуманная инженером конструкция выявляется посредством чертежей. Чертеж — язык техники. Начертательная геометрия — грамматика этого интернационального языка.
ПРЕДМЕТ (основное содержание) курса начертательной геометрии.
1. Метод отображения пространственных фигур на плоскость (построение проекций).
2. Построение с помощью проекций обратимого чертежа. (Обратимый чертеж позволяет воспроизвести оригинал, то есть определить форму и размеры фигуры, изображенной на чертеже).
3. Способы решения на чертеже позиционных и метрических задач. Позиционные задачи — на определение взаимного расположения фигур. Метрические задачи — на определение метрических характеристик геометрических фигур (расстояния, углы).
МЕТОД начертательной геометрии — проецирование пространственных фигур на плоскость.
Центральное проецирование
Наиболее общий случай проецирования осуществляется связкой лучей, исходящих из одной точки (рис. 1).
Аппарат центрального проецирования:
a — плоскость проекций; O Ï a — центр проекций;
A[(A Ï a) Ù (A ¹ O) — проецируемая точка;
[OA) — проецирующий луч;
Aa = [OA) I a — центральная проекция точки А на плоскость a;
la = b(OAB) I a — центральная проекция прямой l на плоскость a.
Обратимости нет. Одна центральная проекция точки не позволяет судить о положении точки в пространстве. Аa = Da
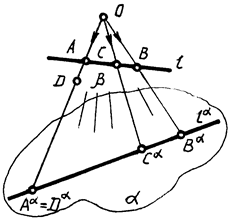 Рис. 1 Рис. 1 |
Параллельное проецирование
Частный случай центрального проецирования с центром проекций, находящимся в бесконечности (в несобственной точке O). Осуществляется связкой лучей заданного направления S (рис. 2).
Аппарат параллельного проецирования:
a -- плоскость проекций;
S — направление проецирования;
[O¥A]½½[O¥B] ¼½½S
Aa = [OA] a — параллельная проекция точки А на плоскость ;
la = b(AAa½½BBa ) I a —параллельная проекция прямой на плоскость a.
Обратимости нет. Одна центральная проекция точки не позволяет судить о положении точки в пространстве. А = D
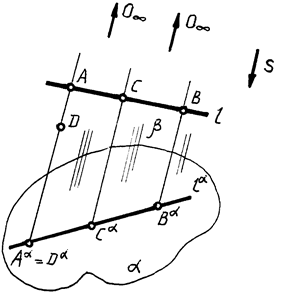 Рис. 2 Рис. 2 |
1.4. Инвариантные свойства параллельного проецирования
Геометрические фигуры проецируются на плоскость проекций, в общем случае, с искажением. Характер искажений зависит от аппарата проецирования и положения проецируемой фигуры относительно плоскости проекций.
В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (искажаются линейные и угловые величины). Некоторые свойства фигуры сохраняются на ее проекции.
Сохраняющиеся в проекции свойства фигуры называются независимыми или ИНВАРИАНТНЫМИ. Эти инвариантные свойства часто называют сокращенно: инварианты.
Инварианты параллельного проецирования
1.Проекция точки есть точка (рис. 1; рис.2)
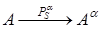
2.Проекция прямой есть прямая (рис. 1; рис.2)
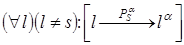 *
*
3. Проекция точки, принадлежащей прямой, принадлежит проекции.
этой прямой (рис. 1; рис.2)
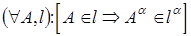
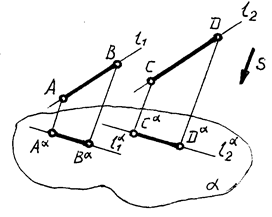
4.Проекция точки пересечения прямых определяется пересечением проекций этих прямых (рис. 3)
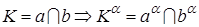
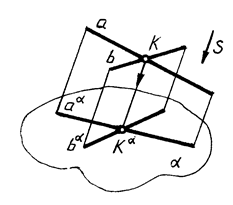
5.Проекции взаимно параллельных прямых взаимно параллельны (рис. 4)
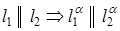
6.Отношение длин отрезков взаимно параллельных прямых равно отношению длин их проекций (рис. 4)
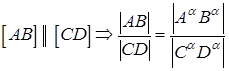
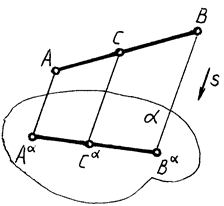
СЛЕДСТВИЕ: если отрезок прямой делится точкой в каком-либо отношении, то проекция отрезка делится проекцией этой точки в том же отношении (рис. 5)
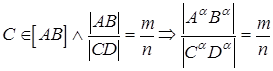
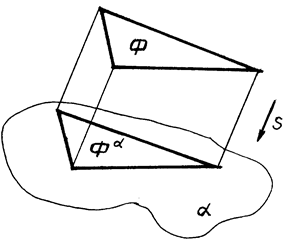
7. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость в конгруэнтную фигуру (рис. 6)
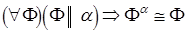
| Рис. 3 Рис. 4 |
| Рис. 5 Рис. 6 |
