Введение. методы проецирования
ВВЕДЕНИЕ. МЕТОДЫ ПРОЕЦИРОВАНИЯ
План:
1.1. Введение. Предмет и метод начертательной геометрии
1.2. Центральное проецирование
1.3. Параллельное проецирование
1.4. Инвариантные свойства параллельного проецирования
1.5. Прямоугольное (ортогональное) проецирование
Введение. Предмет и метод начертательной геометрии
Начертательная геометрия — теоретическая база для составления чертежей.
“Паук совершает операции, напоминающие операции ткача, и пчела постройкой своих восковых ячеек посрамляет некоторых людей-архитекторов. Но и самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что прежде чем строить ячейку из воска, он уже состроил ее в своей голове”(К.Маркс, “Капитал”, т.1, с.189).
Задуманная инженером конструкция выявляется посредством чертежей. Чертеж — язык техники. Начертательная геометрия — грамматика этого интернационального языка.
ПРЕДМЕТ (основное содержание) курса начертательной геометрии.
1. Метод отображения пространственных фигур на плоскость (построение проекций).
2. Построение с помощью проекций обратимого чертежа. (Обратимый чертеж позволяет воспроизвести оригинал, то есть определить форму и размеры фигуры, изображенной на чертеже).
3. Способы решения на чертеже позиционных и метрических задач. Позиционные задачи — на определение взаимного расположения фигур. Метрические задачи — на определение метрических характеристик геометрических фигур (расстояния, углы).
МЕТОД начертательной геометрии — проецирование пространственных фигур на плоскость.
Центральное проецирование
Наиболее общий случай проецирования осуществляется связкой лучей, исходящих из одной точки (рис. 1).
Аппарат центрального проецирования:
a — плоскость проекций; O Ï a — центр проекций;
A[(A Ï a) Ù (A ¹ O) — проецируемая точка;
[OA) — проецирующий луч;
Aa = [OA) I a — центральная проекция точки А на плоскость a;
la = b(OAB) I a — центральная проекция прямой l на плоскость a.
Обратимости нет. Одна центральная проекция точки не позволяет судить о положении точки в пространстве. Аa = Da
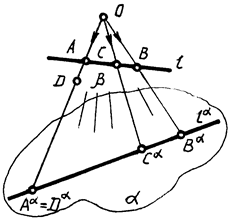 Рис. 1 Рис. 1 |
Параллельное проецирование
Частный случай центрального проецирования с центром проекций, находящимся в бесконечности (в несобственной точке O). Осуществляется связкой лучей заданного направления S (рис. 2).
Аппарат параллельного проецирования:
a -- плоскость проекций;
S — направление проецирования;
[O¥A]½½[O¥B] ¼½½S
Aa = [OA] a — параллельная проекция точки А на плоскость ;
la = b(AAa½½BBa ) I a —параллельная проекция прямой на плоскость a.
Обратимости нет. Одна центральная проекция точки не позволяет судить о положении точки в пространстве. А = D
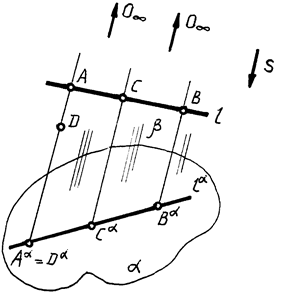 Рис. 2 Рис. 2 |
1.4. Инвариантные свойства параллельного проецирования
Геометрические фигуры проецируются на плоскость проекций, в общем случае, с искажением. Характер искажений зависит от аппарата проецирования и положения проецируемой фигуры относительно плоскости проекций.
В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (искажаются линейные и угловые величины). Некоторые свойства фигуры сохраняются на ее проекции.
Сохраняющиеся в проекции свойства фигуры называются независимыми или ИНВАРИАНТНЫМИ. Эти инвариантные свойства часто называют сокращенно: инварианты.
Инварианты параллельного проецирования
1.Проекция точки есть точка (рис. 1; рис.2)
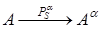
2.Проекция прямой есть прямая (рис. 1; рис.2)
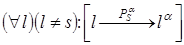 *
*
3. Проекция точки, принадлежащей прямой, принадлежит проекции.
этой прямой (рис. 1; рис.2)
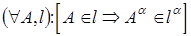
4.Проекция точки пересечения прямых определяется пересечением проекций этих прямых (рис. 3)
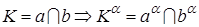
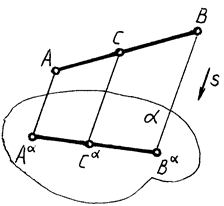
5.Проекции взаимно параллельных прямых взаимно параллельны (рис. 4)
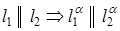
6.Отношение длин отрезков взаимно параллельных прямых равно отношению длин их проекций (рис. 4)
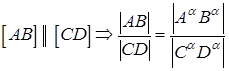
СЛЕДСТВИЕ: если отрезок прямой делится точкой в каком-либо отношении, то проекция отрезка делится проекцией этой точки в том же отношении (рис. 5)
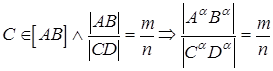
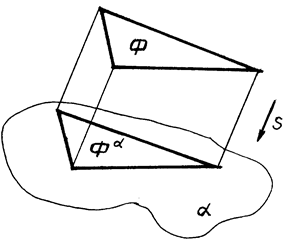
7. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость в конгруэнтную фигуру (рис. 6)
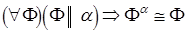
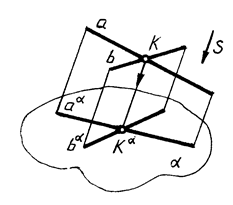
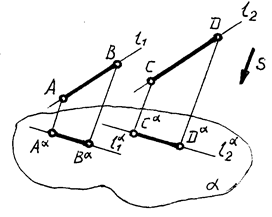
| Рис. 3 Рис. 4 |
| Рис. 5 Рис. 6 |
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
В основу составления технических чертежей положен способ прямоугольных проекций. Предмет проецируют на взаимно перпендикулярные плоскости, при этом каждую его сторону изображают отдельно, затем плоскости проекций совмещают в одну.
На рис. аа даны три плоскости проекций: H — горизонтальная, V — фронтальная и W — профильная, пересекающиеся под прямым углом по линиям x, у и z, которые называют осями проекций (осями координат). Точку О — пересечения осей называют началом координат.
При проецировании изображаемый предмет располагают между глазом наблюдателя и соответствующей плоскостью проекций. На каждой плоскости проекций можно получить измерения только под двум осям, а по третьей оси, параллельно которой ведется проецирование, сливается в точку.
Изображение на фронтальной плоскости называют фронтальной проекцией, на горизонтальной плоскости — горизонтальной проекцией, на профильной - профильной проекцией.
В практике изображение обращенной к наблюдателю видимой части поверхности предмета называют видом.Каждый вид несет свою информацию. На видах должно быть показаны и невидимые линии (отверстие в детали, например).
За основные плоскости проекций принимают шесть граней куба.
Совмещение граней куба с плоскостью показано на рис. .
Наименование видов на чертежах не записывают. Виды располагают не произвольно, а на общих линиях- линиях проекционной связи.
Количество видов на чертеже для данного предмета должно быть наименьшим, но обеспечивающим полную ясность чертежа.
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
План:
2.1. Общие положения
2.2. Аксонометрическое проецирование
2.3. Коэффициенты искажения
2.4. Виды аксонометрических проекций
2.5. Стандартные аксонометрические проекции
Общие положения
Аксонометрическая проекция — один из способов изображения пространственных фигур на плоскости. Этот вид проекций обладает большой наглядностью и является обратимым изображением. Слово “аксонометрия”в переводе с греческого означает “измерение по осям”.
Коэффициенты искажения
Искажение отрезков осей координат при их проецировании на картинную плоскость характеризуется коэффициентами искажений по аксонометрическим осям.
Коэффициентом искажения называется отношение длины аксонометрической проекции отрезка оси к его натуральной длине.
Коэффициенты искажения по осям Ooxo, Ooyo и Oozo соответственно будут равны:
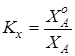 ;
; 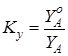 ;
; 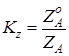 .
.
Комплексный чертеж точки
Внутри трехгранного угла, образованного горизонтальной (H), фронтальной (V) и профильной (W) плоскостями проекций, расположим какую-либо точку А (рис. 13).
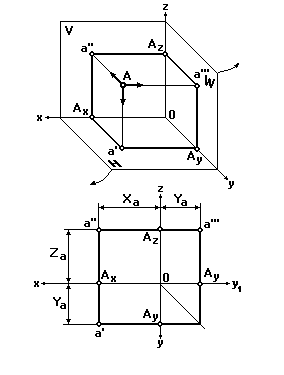
| Рис. 13 |
Направим проецирующий луч перпендикулярно плоскости V. Точка пересечения этого луча с плоскостью V будет фронтальной проекцией a'' точки A. Спроецируем точку А на плоскость H и получим ее горизонтальную проекцию a'. Проецируя точку А на плоскость W, получим ее профильную проекцию a'''.
Для получения чертежа необходимо все три плоскости V, H и W вместе с построенными на них проекциями совместить в одну плоскость, т.е. развернуть их.
При этом плоскость H поворачивается вокруг оси x на 90 градусов книзу, плоскость W — вокруг оси z на 90 градусов вправо, а плоскость V остается неподвижной (при этом ось y как бы раздваивается).
В результате совмещения получают чертеж точки в трех проекциях. Очертания плоскостей H, V и W на чертеже не показывают.
Линию, связывающую горизонтальную и профильную проекции точки А, представляют двумя отрезками ломаной линии. Вершина ее лежит на биссектрисе угла, образованного осями y и y1. Эту биссектрису называют постоянной линией чертежа.
Прямые линии, соединяющие проекции точки и перпендикулярные осям проекций, называют линиями проекционной связи (рис. ).
Координатный отрезок, равный превышению точки А над плоскостью H, называют высотой Za (аппликатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости V, называют глубиной Ya (ординатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости W, называют широтой Xa (абсциссой) точки А.
Горизонтальная проекция точки А определяется на эпюре ее координатами Xa и Ya, а фронтальная — координатами Xa и Za (рис. 13).
Проекции прямых уровня
Прямыми уровня называются прямые, параллельные плоскостям проекций. Их основное свойство: отрезки, принадлежащие прямым уровня, на одной из плоскостей проекций (параллельной им) изображаются в натуральную величину, а на второй плоскости проекций изображаются отрезками, параллельными осям.
Угол наклона прямой уровня к одной из плоскостей проекций на другой плоскости проекций изображается в натуральную величину.
Горизонталь — прямая равных высот (рис. 16)
Это прямая (h), параллельная горизонтальной плоскости проекций.
Поскольку все точки горизонтали одинаково удалены от плоскости H, то фронтальная проекция горизонтали параллельна оси x, а горизонтальная проекция горизонтали равна натуральной величине проецируемого отрезка горизонтали (отмечено Н.В.).
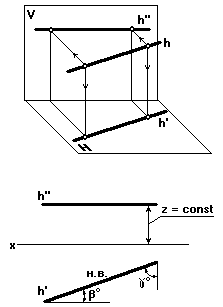
| Рис. 16 |
Угол b— угол наклона горизонтали к фронтальной плоскости проекций, а угол g— к профильной плоскости проекций, причем
Ðb + Ðg = 90o (рис. 16).
Фронталь — прямая равных глубин (рис. 17)
Это прямая (v), параллельная фронтальной плоскости проекций. Так как все точки фронтали одинаково удалены от вертикальной плоскости V, то горизонтальная проекция фронтали равна натуральной величине проецируемого отрезка фронтали (отмечено Н.В.).
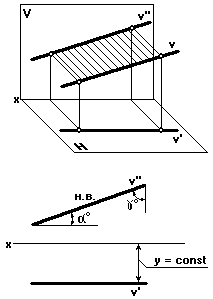
| Рис. 17 |
Угол a — угол наклона фронтали к горизонтальной плоскости проекций, а угол g — к профильной плоскости проекций, причем
Ða + Ðg = 90o (рис. 17).
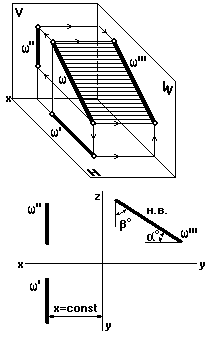
Профильная прямая — прямая равных широт (рис. 18)
Это прямая (w), параллельная профильной плоскости проекций.
Поскольку все точки профильной прямой одинаково удалены от плоскости проекций W, то горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси x, а профильная проекция равна натуральной величине проецируемого отрезка этой прямой (отмечено Н.В.) (рис. 18).
| Рис. 18 |
Углы a и b — углы наклона профильной прямой к горизонтальной (H) и фронтальной (V) плоскостям проекций, причем
Ða + Ðb = 90o.
Параллельные прямые
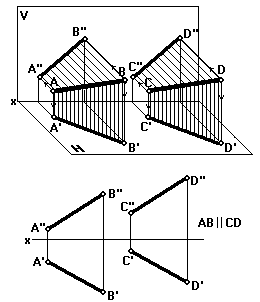
Если провести через данные параллельные прямые АВ и СD плоскости, перпендикулярные горизонтальной плоскости проекций, то эти две плоскости будут параллельны, и в их пересечении с плоскостью H будут получены две взаимно параллельные прямые A'B' и C'D', являющиеся ортогональными проекциями данных прямых АВ и CD на горизонтальную плоскость проекций (рис. 25).
| Рис. 25 |
Аналогичным образом можно получить и ортогональные проекции данных прямых на фронтальную плоскость V.
На комплексном чертеже одноименные проекции параллельных прямых параллельны: A'B' C'D' и A''B'' C''D'' (рис. 25).
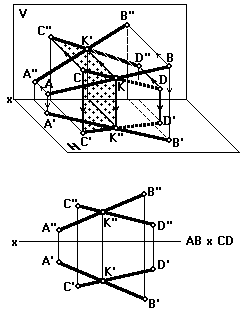
Пересекающиеся прямые
Взаимно пересекающиеся прямые имеют общую точку, например, отрезки прямых АВ и CD пересекаются в точке К. Проекции пересекающихся прямых пересекаются, и точки их пересечения (K' и K'') лежат на одной линии связи — перпендикуляре к оси x (рис. 26).
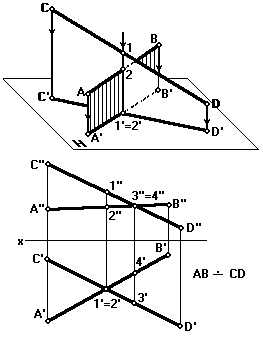
Скрещивающиеся прямые
Это прямые, которые не параллельны и не пересекаются. На комплексном чертеже проекции скрещивающихся прямых (прямые АВ и CD) могут пересекаться, но точки пересечения (1,2 и 3,4) лежат на разных линиях связи (рис. 27). Точкам пересечения одноименных проекций скрещивающихся прямых соответствуют в пространстве две точки: в одном случае — 1 и 2, а в другом — 3 и 4, расположенные на прямых. На чертеже точке пересечения горизонтальных проекций прямых соответствует две фронтальные проекции точек 1'' и 2''. Аналогично — с точками 3 и 4.
 |
| Рис. 26 Рис. 27 |
5. ПЛОСКОСТЬ
План:
5.1. Проекции плоскостей общего положения
5.2. Проекции плоскостей уровня
Горизонтальная плоскость
Фронтальная плоскость
Профильная плоскость
5.3. Проекции проецирующих плоскостей
Горизонтально-проецирующая плоскость
Фронтально-проецирующая плоскость
Профильно-проецирующая плоскость
5.4. Взаимное расположение двух плоскостей
Параллельные плоскости
Пересекающиеся плоскости
5.5. Пересечение плоскостей общего положения
5.6. Взаиморасположение прямой и плоскости
Прямая - в плоскости
Прямая, параллельная плоскости
Прямая пересекает плоскость
5.7. Пересечение прямой с плоскостью
5.8. Условие видимости на чертеже
Проекции плоскостей уровня
Плоскостями уровня называются плоскости, параллельные плоскостям проекций.
Характерная особенность этих плоскостей состоит в том, что элементы, расположенные в этих плоскостях, проецируются на соответствующую плоскость проекций в натуральную величину.
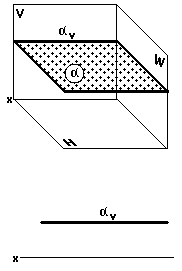
Горизонтальная плоскость (рис. 30)
Горизонтальная плоскость параллельна горизонтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.
На рис. 30 изображена горизонтальная плоскость a (aV).
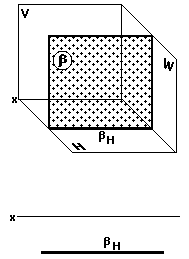
Фронтальная плоскость (рис. 31)
Фронтальная плоскость параллельна фронтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним горизонтальным следом, параллельным оси x.
На рис.31 изображена фронтальная плоскость b (bH).
  |
| Рис. 30 Рис. 31 |
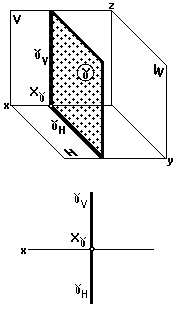
Профильная плоскость (рис. 32)
Профильная плоскость параллельна профильной плоскости проекций.
На двухкартинном комплексном чертеже она изображается двумя следами: горизонтальным и фронтальным, перпендикулярными оси x.
На рис.32 изображена профильная плоскость g (gH,V).
| Рис. 32 |
Главные линии плоскости
Кроме прямых линий общего положения, в плоскости отмечают три главные линии: горизонтальную (горизонталь), фронтальную (фронталь) и линию наибольшего наклона. Эти линии применяют как вспомогательные: они упрощают решение задач. Две из них — горизонтальная и фронтальная — уже рассматривались.
*Необходимо добавить, что все горизонтальные линии плоскости параллельны между собой, а их горизонтальные проекции параллельны горизонтальному следу плоскости (рис. 62). Горизонтальный след плоскости — одна из горизонталей.
*Все фронтальные линии плоскости параллельны между собой, а их фронтальные проекции параллельны фронтальному следу плоскости. Фронтальный след плоскости — одна из фронтальных линий (рис. 63).
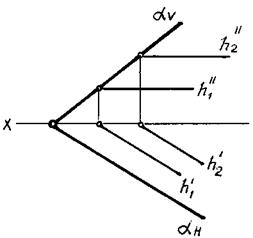 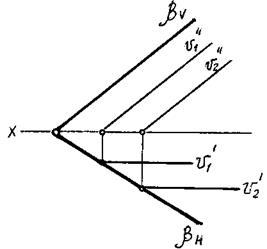 Рис. 62 Рис. 63 Рис. 62 Рис. 63 |
Линии наибольшего наклона плоскости
Прямую, лежащую в плоскости и имеющую наибольший угол с той или друго плоскостью проекций, называют линией наибольшего наклона (ЛНН).
Линии наибольшего наклона плоскости перпендикулярны к ее следам или к линиям уровня (либо к ее горизонталям, либо к фронталям, либо к ее профильным прямым) (рис. 64).
В случае перпендикулярности к горизонтали определяется наклон к плоскости проекций H (при этом ЛНН называют линией наибольшего ската), перпендикулярности к фронтали — наклон к плоскости проекций V, перпендикулярности к профильной прямой — наклон к плоскости проекций W.
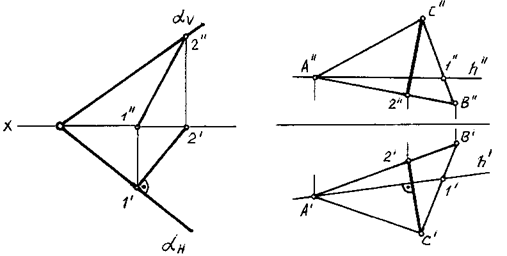 Рис. 64 Рис. 64 |
На рис. 65, 66 дано изображение плоскости a (а || b), для которой требуется построить линию наибольшего наклона к горизонтальной плоскости проекций H.
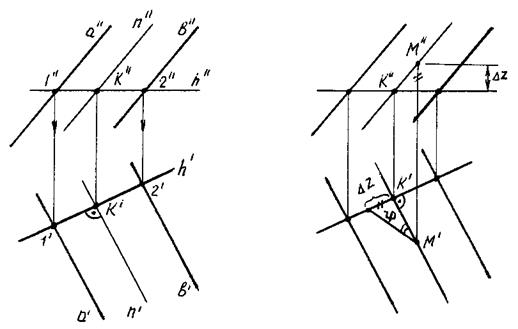
Рис. 65
Проведем в данной плоскости горизонталь h (рис. 66). Прямая n, перпендикулярная к прямой h, перпендикулярна и к следу плоскости aH (KL^H) (рис. ).
Угол наклона прямой n к плоскости H определяется как угол между прямой и ее проекцией на плоскость H. Строим КК'^H (рис. 66). Тогда угол j — искомый угол наклона прямой n к плоскости H.
На рис. построена линия наибольшего наклона плоскости a к горизонтальной плоскости проекций — прямая n. Угол наклона плоскости a к плоскости H получают при определении натуральной величины отрезка КМ при построении прямоугольного треугольника по проекциям K'M' и K”.
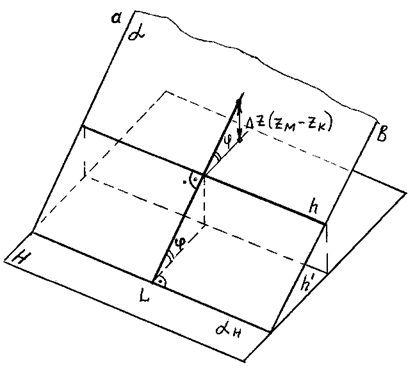
Рис. 66
Перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Построение таких плоскостей может быть выполнено двумя путями:
1) плоскость проводится через перпендикуляр к другой;
2) плоскость проводится перпендикулярно прямой, принадлежащей другой плоскости.
На рис. 70 изображены прямая общего положения l и плоскость общего положения a (а ´ b). Требуется построить через прямую l плоскость, перпендикулярную к плоскости a.
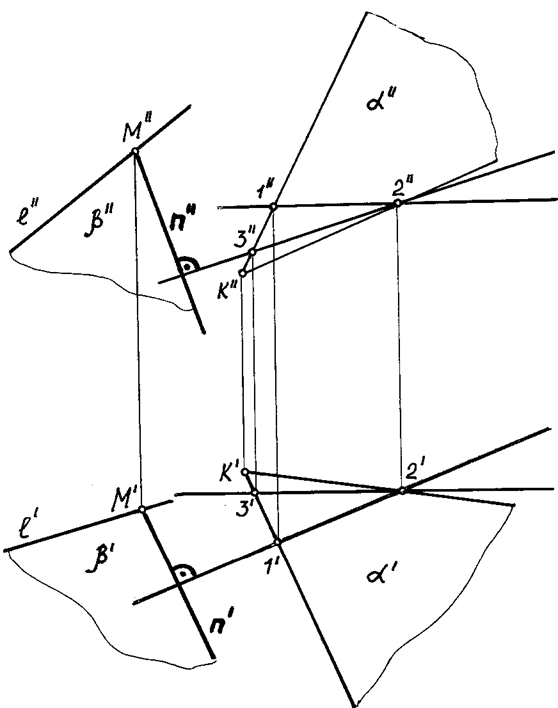
Рис. 70
Для решения задачи необходимо через какую-нибудь точку данной прямой, например, точку М, провести перпендикуляр к плоскости a, заданной пересекающимися прямыми a и b.
Проводим в плоскости a горизонталь h и фронталь v (рис. 70).
Далее из точки М, взятой на прямой l, опускаем перпендикуляр n, пользуясь рассмотренным выше положением: n' ^ h'; n'' ^ v'', т.е. горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная его проекция — перпендикулярна фронтальной проекции фронтали (рис. 70).
Плоскость b (l ´ n), проходящая через прямую n, будет перпендикулярна к плоскости a.
Перпендикулярные прямые
Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.
На рис. 71 изображена прямая l общего положения, к которой требуется провести перпендикулярную прямую.
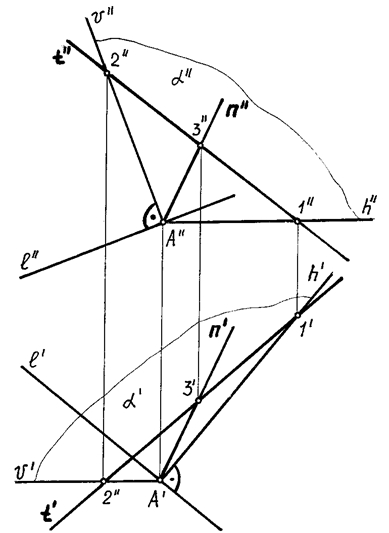
Рис. 71
Через точку А прямой l строим перпендикулярную к ней плоскость a (h ´ v):
l' ^ h'; l'' ^ h'' (рис. 71).
Любая прямая, лежащая в плоскости a будет также перпендикулярна к данной прямой l. Поэтому проведем в этой плоскости произвольную прямую t, на которой возьмем произвольную точку, например, точку В (рис. 71).
Соединив точки А и В, лежащие в плоскости , получим прямую n, перпендикулярную к данной прямой l (рис. 71).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1) Что называется линией наибольшего наклона плоскости?
Основы теории теней
Нанесением теней пользуются для придания проекционным чертежам большей наглядности. Особенно широко используются тени при оформлении архитектурных проектов, а также для решения ряда практических задач (например, для выявления освещенности наружных или внутренних частей сооружения при определенных условиях, для определения размеров сооружения по отбрасываемой им тени и т.п.).
Различают собственные и падающие тени.
СОБСТВЕННОЙназывается тень, которая получается на неосвещенной поверхности предмета (или объекта) при освещении его каким-либо источником света (рис. 72).
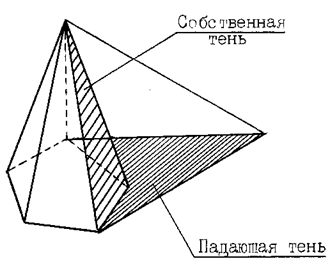
Рис. 72
ПАДАЮЩЕЙназывается тень, отбрасываемая предметом на плоскости проекций, или возникающая на поверхности предмета из-за того, что на пути лучей света расположен другой предмет.
Если предмет освещается источником света, находящимся на конечном расстоянии от него (факелом, лампой, свечой), то совокупность световых лучей, падающих на предмет, образует конус или пирамиду. Такая тень называется ФАКЕЛЬНОЙ.
Если же источник света находится в бесконечности, то совокупность световых лучей образует цилиндр или призму. Тень при этих условиях называется СОЛНЕЧНОЙ.
НАПРАВЛЕНИЕ СВЕТОВЫХ ЛУЧЕЙ. При построении теней в ортогональных проекциях, направление l лучей света обычно принимают параллельным диагонали куба, грани которого параллельны плоскостям проекций (рис. 73).
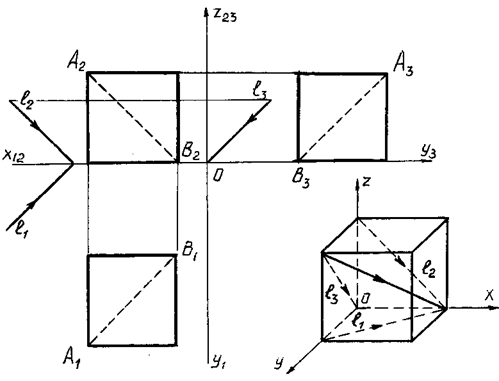
Рис. 73
Диагональ куба АВ образует с плоскостями проекций углы, равные 35о16', а проекции ее наклонены к плоскостям H, V, и W под углом 45o.
При построении теней в аксонометрии, направление лучей света, параллельное диагонали куба, не всегда дает удачное расположение светотеней; в таких случаях следует выбрать другое направление, обеспечивающее выразительность чертежа.
Метод обратных лучей
Метод обратных лучей успешно применяется при построении теней, падающих от одной геометрической фигуры на другую, и характеризуется следующими построениями:
а) строятся тени, падающие от обеих заданных фигур на какую-либо плоскость;
б) выявляются точки пересечения теней от двух линий, из которых одна принадлежит контуру первой фигуры, а другая — контуру второй;
в) при помощи обратных лучей (то есть лучей, параллельных лучам света, но имеющих обратное направление) “возвращаются” эти точки в пространство (на соответствующие контурные линии фигур);
г) с помощью полученных точек определяется искомая тень, падающая от одной фигуры на другую.
ПРИМЕР.
На рис. 86 показано применение метода обратных лучей на
примере построения падающей тени от прямой на плоскость треугольника.
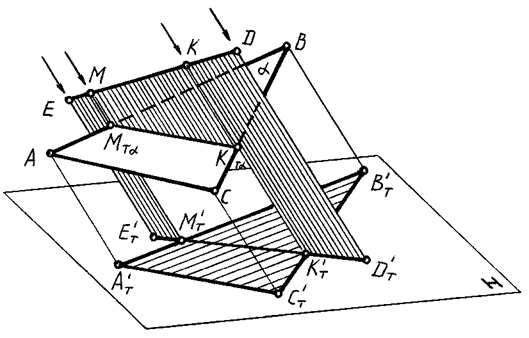
Рис. 86
Построены падающие тени от треугольника АВС и от прямой ED на плоскость Н. Через точки МT' и МT', общие теням прямой ED и сторонам АВ и ВС, проведены обратные лучи, пересекающие указанные прямые соответственно в точках М', М'', К' и K''. Точки М' и K' представляют собой тени от точек M'' и K'' прямой ЕD на стороны АВ и ВС. Искомая же тень будет определена точками M'K'.
На рис. 87 приведено решение этой задачи в ортогональных проекциях.
. 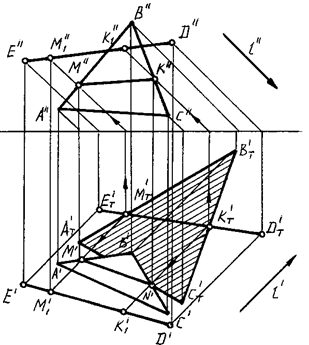
Рис. 87
2. Метод следа светового луча
(метод сечения лучевой плоскостью)
Метод следа луча основан на том, что тень, падающая от точки, есть след проведенного через нее луча.
На рисунке 88 приведено решение задачи на построение тени от прямой АВ на плоскость Q (CDEF) в ортогональных проекциях методом следа луча (или сечения лучевой плоскости).
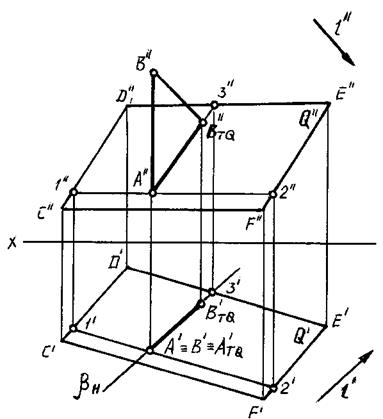
Рис. 88
В данном случае тень от прямой АВ на плоскость Q построена с помощью двух точек АTQ(АTQ',АTQ'') и ВTQ(ВTQ',ВTQ''), в которых пересекаются с плоскостью Q(CDEF) соответственно данная прямая и световой луч, проходящий через точку В.
Плоскость b ^ H является лучевой плоскостью, которая проводится через луч ВВTQ для определения точки ВTQ(ВTQ',ВTQ'').
Тени геометрических тел
Выше говорилось, что тени делятся на собственные и падающие. Определение собственной тени сводится к нахождению ее контуров, то есть линий, отделяющих освещенную часть поверхности от неосвещенной.
Контур падающей тени можно рассматривать как тень, падающую от контура собственной тени.
Тени многогранников
На рисунке 89, 90 построены собственная и падающая тени прямой пятиугольной призмы.
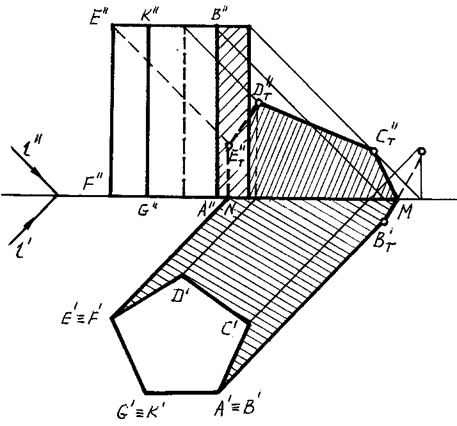
Рис. 89
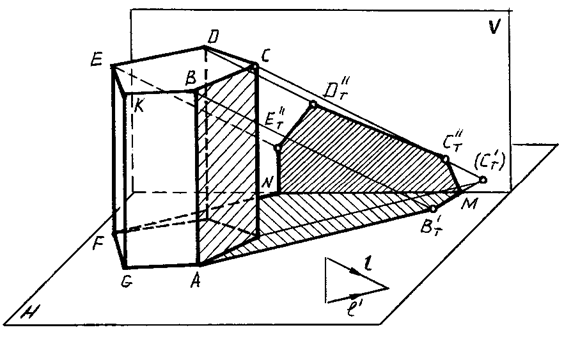
Рис. 90
Для определения контура собственной тени призмы необходимо установить освещенность ее граней. Так как боковые грани призмы перпендикулярны к плоскости Н, то их освещенность легко определить на горизонтальной проекции, где видно, что обращены к свету две грани: EFGK и KGAB.
Освещено также верхнее основание призмы.
Таким образом, контуром собственной тени является ломаная ABCDEFGA, от которой построена тень, падающая на плоскости H и V по правилам, изложенным в предыдущей теме.
На рисунке 91,92 приведен пример построения собственной и падающей теней правильной пятиугольной пирамиды SABCDE.
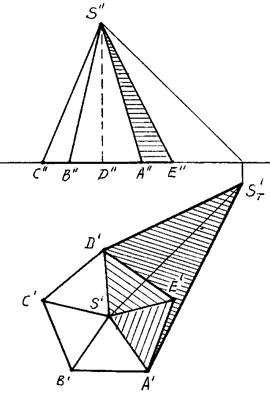
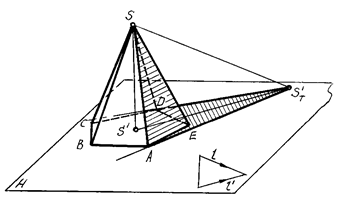
Рис. 91 Рис. 92
В отличие от прямой призмы, боковые грани пирамиды не являются горизонтально-проецирующими плоскостями, поэтому определить их освещенность непосредственно по горизонтальной проекции не всегда возможно.
Строим падающую тень ST' от вершины S на плоскость Н и определяем падающие тени от боковых ребер пирамиды. Линиями контура падающей тени пирамиды оказались прямые ST'А и ST'D. Следовательно, контур собственной тени пройдет вдоль ребер SA и SD. Таким образом, в собственной тени будут находиться грани SAE, SDE и основание пирамиды.
Тени цилиндра
Чтобы построить контур собственной тени цилиндрической поверхности, необходимо провести к этой поверхности касательные лучевые плоскости, параллельные направлению лучей света, и найти линии касания (образующие цилиндра). Вдоль этих образующих пройдет контур собственной тени.
На рисунке 93 приведен пример построения собственной и падающей теней вертикально расположенного прямого кругового цилиндра. Контур собственной тени цилиндра проходит вдоль образующих АВ и CD и замыкается сверху полуокружностью АМС верхнего основания, а снизу — полуокружностью BND нижнего основания.
Контур падающей тени от цилиндра состоит из падающих теней от образующих АВ и СD и падающих теней от полуокружностей АМС и BND.
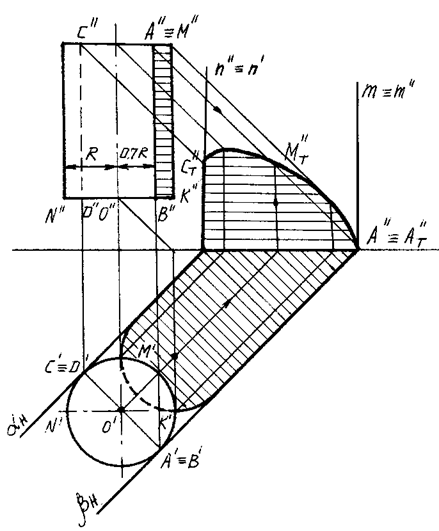
Рис. 93
Падающие тени от образующих АВ и СD определяются с помощью следов aH, m, bH и n, касательных лучевых плоскостей a и b. Тени, падающие от полуокружностей АМС и BND, определяются как в примерах предыдущей темы (рис. 85).
Собственную тень на вертикальном круговом цилиндре в ортогональных проекциях можно построить, не имея горизонтальной проекции цилиндра, так как известно, что расстояние от фронтальных проекций образующих АВ и CD до фронтальной проекции оси цилиндра равно радиусу цилиндр, умноженному на косинус 45о, то есть:
O'B' = O'D' = 0,707 O''K'' (рис. 93).
Графическим путем проекции В'' и D'' точек B и D можно найти следующим образом (рис. 93): из точек O'' и K'' проводим под углом 45 градусов к отрезку O''K'' прямые — катеты прямоугольного треугольника O''1 K''. Из точки O'' радиусом O''1 проводим полуокружность, пересекающую прямую N''K'' в искомых точках B'' и D''.
Тени конуса
На рис. 94, 95 выполнены построения собственной и падающей теней конуса.
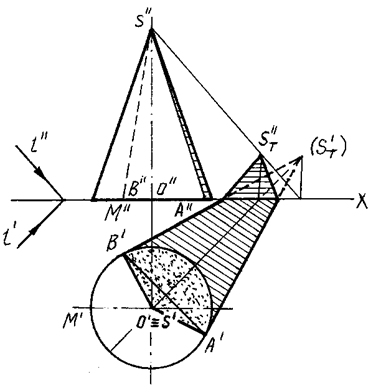
Рис. 94
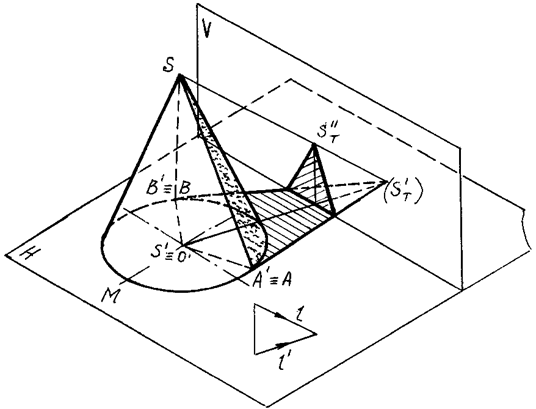
Рис. 95
Вначале определяется тень ST' (мнимая), падающая от вершины S конуса на плоскость его основания Н; из полученной точки проводятся прямые, касательные к основанию конуса, и определяются точки касания А и В. Через эти точки проводятся образующие SA и SB, которые вместе с дугой основания АМВ образуют контур собственной тени.
Касательные ST'A' и ST'B' к основанию на рис. 94, 95 являются линиями контура падающей тени конуса. Однако, это справедливо лишь в том случае, если конус стоит на плоскости, на которую падает тень. На рисунке падающая тень имеет точки изломов на оси ОХ.
7.4. Тени геометрических тел
Выше говорилось, что тени делятся на собственные и падающие. Определение собственной тени сводится к нахождению ее контуров, то есть линий, отделяющих освещенную часть поверхности от неосвещенной.
Контур падающей тени можно рассматривать как тень, падающую от контура собственной тени.
Тени многогранников
На рисунке 89, 90 построены собственная и падающая тени прямой пятиугольной призмы.
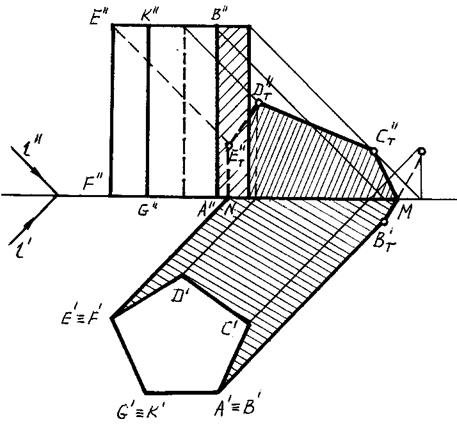
Рис. 89
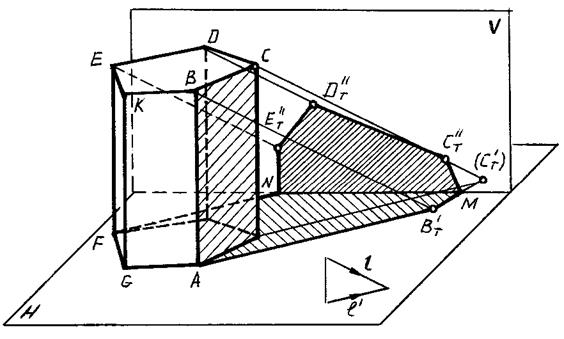
Рис. 90
Для определения контура собственной тени призмы необходимо установить освещенность ее граней. Так как боковые грани призмы перпендикулярны к плоскости Н, то их освещенность легко определить на горизонтальной проекции, где видно, что обращены к свету две грани: EFGK и KGAB.
Освещено также верхнее основание призмы.
Таким образом, контуром собственной тени является ломаная ABCDEFGA, от которой построена тень, падающая на плоскости H и V по правилам, изложенным в предыдущей теме.
На рисунке 91,92 приведен пример построения собственной и падающей теней правильной пятиугольной пирамиды SABCDE.
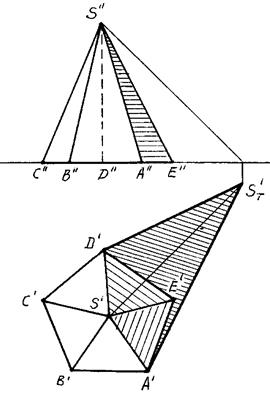
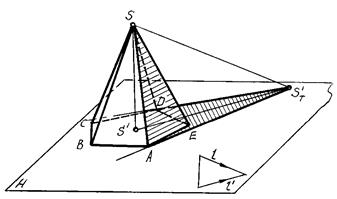
Рис. 91 Рис. 92
В отличие от прямой призмы, боковые грани пирамиды не являются горизонтально-проецирующими плоскостями, поэтому определить их освещенность непосредственно по горизонтальной проекции не всегда возможно.
Строим падающую тень ST' от вершины S на плоскость Н и определяем падающие тени от боковых ребер пирамиды. Линиями контура падающей тени пирамиды оказались прямые ST'А и ST'D. Следовательно, контур собственной тени пройдет вдоль ребер SA и SD. Таким образом, в собственной тени будут находиться грани SAE, SDE и основание пирамиды.
Тени цилиндра
Чтобы построить контур собственной тени цилиндрической поверхности, необходимо провести к этой поверхности касательные лучевые плоскости, параллельные направлению лучей света, и найти линии касания (образующие цилиндра). Вдоль этих образующих пройдет контур собственной тени.
На рисунке 93 приведен пример построения собственной и падающей теней вертикально расположенного прямого кругового цилиндра. Контур собственной тени цилиндра проходит вдоль образующих АВ и CD и замыкается сверху полуокружностью АМС верхнего основания, а снизу — полуокружностью BND нижнего основания.
Контур падающей тени от цилиндра состоит из падающих теней от образующих АВ и СD и падающих теней от полуокружностей АМС и BND.
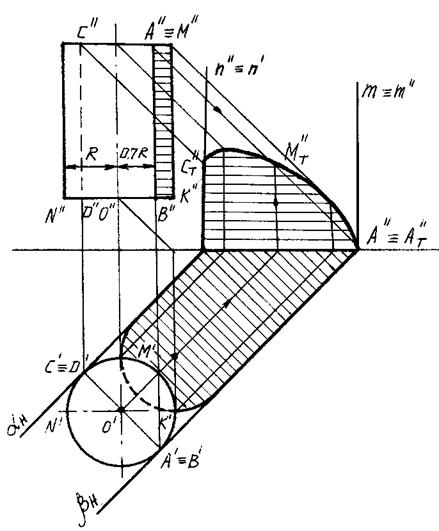
Рис. 93
Падающие тени от образующих АВ и СD определяются с помощью следов aH, m, bH и n, касательных лучевых плоскостей a и b. Тени, падающие от полуокружностей АМС и BND, определяются как в примерах предыдущей темы (рис. 85).
Собственную тень на вертикальном круговом цилиндре в ортогональных проекциях можно построить, не имея горизонтальной проекции цилиндра, так как известно, что расстояние от фронтальных проекций образующих АВ и CD до фронтальной проекции оси цилиндра равно радиусу цилиндр, умноженному на косинус 45о, то есть:
O'B' = O'D' = 0,707 O''K'' (рис. 93).
Графическим путем проекции В'' и D'' точек B и D можно найти следующим образом (рис. 93): из точек O'' и K'' проводим под углом 45 градусов к отрезку O''K'' прямые — катеты прямоугольного треугольника O''1 K''. Из точки O'' радиусом O''1 проводим полуокружность, пересекающую прямую N''K'' в искомых точках B'' и D''.
Тени конуса
На рис. 94, 95 выполнены построения собственной и падающей теней конуса.
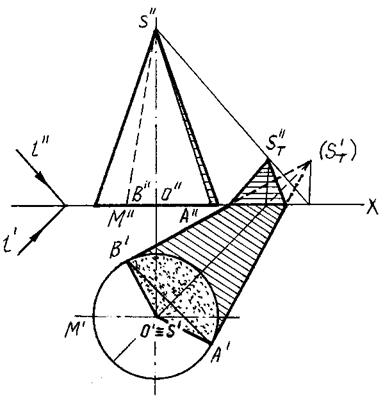
Рис. 94
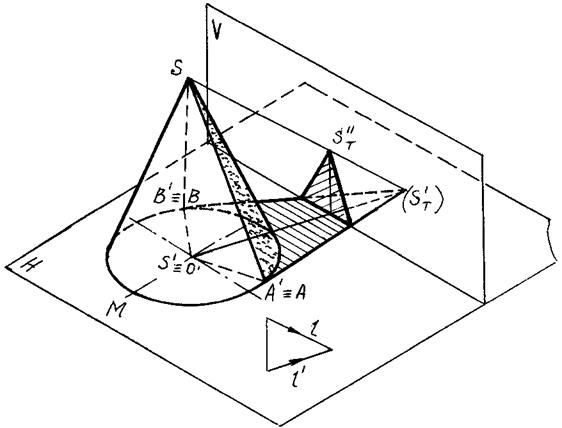
Рис. 95
Вначале определяется тень ST' (мнимая), падающая от вершины S конуса на плоскость его основания Н; из полученной точки проводятся прямые, касательные к основанию конуса, и определяются точки касания А и В. Через эти точки проводятся образующие SA и SB, которые вместе с дугой основания АМВ образуют контур собственной тени.
Касательные ST'A' и ST'B' к основанию на рис. 94, 95 являются линиями контура падающей тени конуса. Однако, это справедливо лишь в том случае, если конус стоит на плоскости, на которую падает тень. На рисунке падающая тень имеет точки изломов на оси ОХ.
Построение теней в нишах
ПРИМЕР 1. На рис. 98, 99 в аксонометрии и в ортогональных проекциях изображена прямоугольная ниша, в которой необходимо построить собственные и падающие тени.
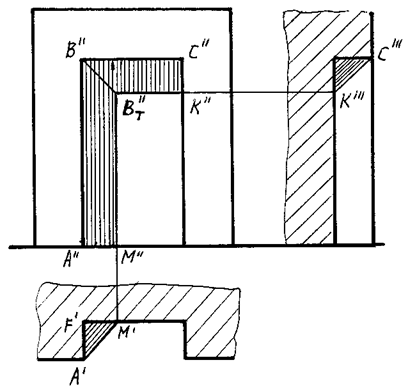
Рис. 98
Расположение граней таково, что в собственной тени находятся левая боковая и верхняя грани, поэтому собственная тень ограничена ломаной линией ABCDEFA.
Так как отрезки CD, DE, EF, FA являются внутренними ребрами ниши, то они входят одновременно и в контур падающей тени, то есть проходят по границе, отделяющей собственную тень от падающей. Строить падающую тень необходимо лишь от ребер АВ и ВС.
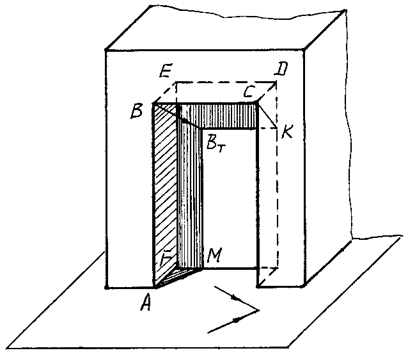
Рис. 99
ПРИМЕР 2. На рис. 100 дана ниша, перекрытая полуциркульной аркой.
Контуром собственной тени в этом примере является линия ABDEFKA, в состав которой входит образующая цилиндра DE. Последняя определяется как линия касания к цилиндрической поверхности арки касательной лучевой плоскостью Q, перпендикулярной к V.
