Решение системы линейных уравнений

Учреждение образования «Белорусская государственная

Сельскохозяйственная академия»

Кафедра высшей математики

Методические указания

по изучению темы «Матричный метод решения систем линейных уравнений» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)

Горки, 2013

Матричный метод решения систем линейных

Уравнений

Обратная матрица

Квадратная матрица 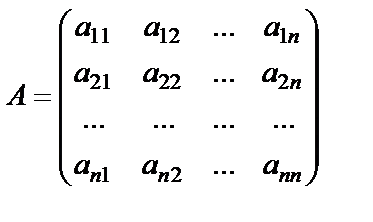порядка n называется невырожденной, если её определитель отличен от нуля. Если же определитель матрицы равен нулю, то матрица называется вырожденной.

Матрица В называется обратной к матрице А, если при умножении её слева и справа на матрицу А получается единичная матрица: 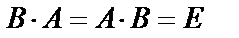. Обозначается обратная матрица .

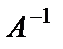Если матрица А невырожденная, то для неё всегда существует обратная матрица 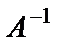и притом единственная.

Составим матрицу 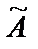из алгебраических дополнений элементов матрицы А: 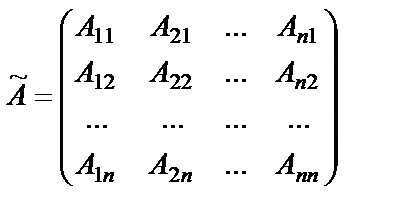. Такая матрица называется союзной матрицей для матрицы А или матрицей, присоединённой к матрице А.

Обратная матрица 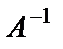определяется по формуле .

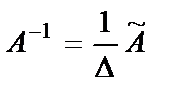Пример 1. Найти матрицу, обратную для матрицы

.

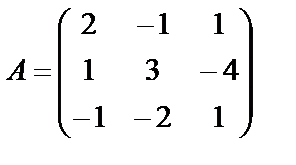Решение. Вычислим определитель матрицы А:

.

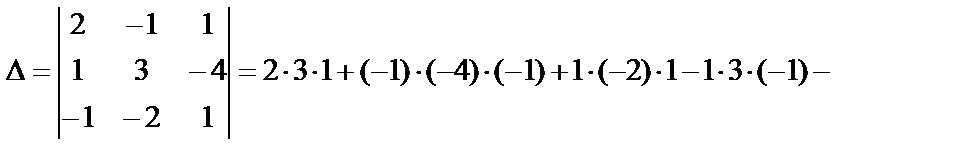
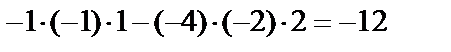Так как определитель матрицы отличен от нуля, то для данной матрицы существует обратная. Найдём матрицу 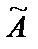, союзную для матрицы А. Для этого вычислим алгебраические дополнения всех элементов матрицы А:

, ,

, ,

, ,

, ,

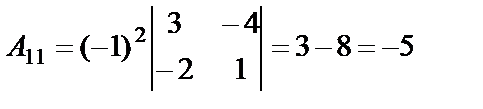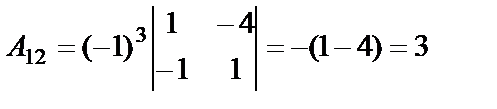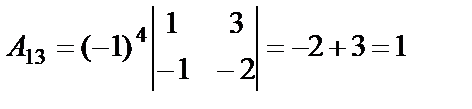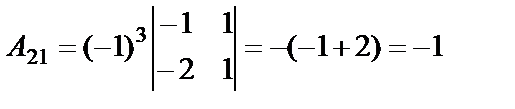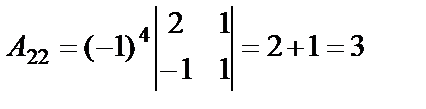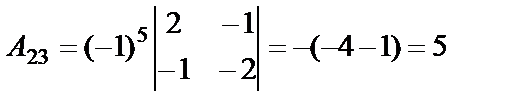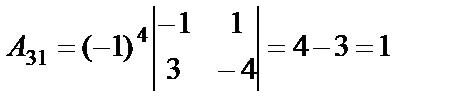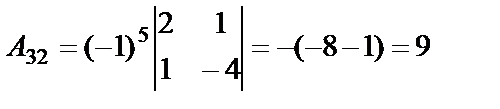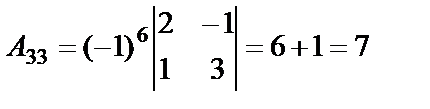. Тогда 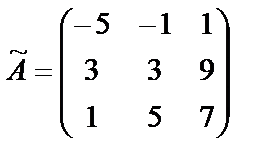и обратная матрица равна 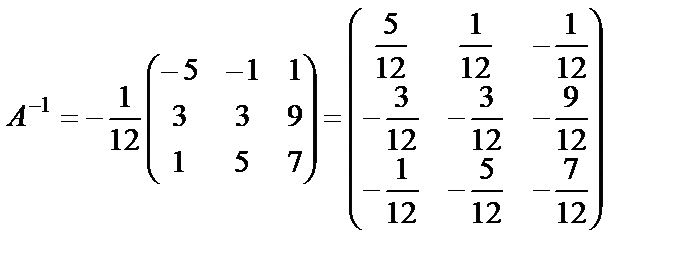. Чтобы убедиться в том, правильно ли найдена обратная матрица, нужно её умножить на матрицу А. Если в результате будет получена единичная матрица, то обратная матрица найдена правильно.

Решение системы линейных уравнений

Рассмотрим систему n линейных уравнений с n неизвестными

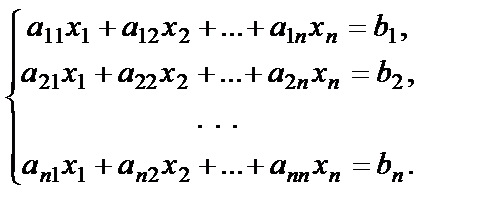
Коэффициенты при неизвестных запишем в виде квадратной матрицы 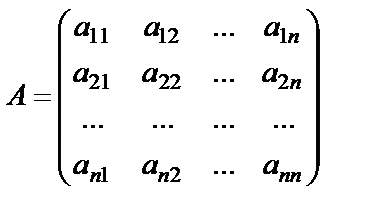, неизвестные – в виде матрицы 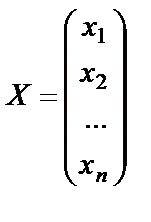и свободные члены – в виде матрицы 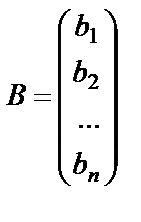. Тогда рассматриваемая система может быть записана в виде 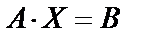. Если определитель матрицы А отличен от нуля, то система имеет единственное решение .

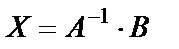Для нахождения решения системы необходимо:

1) найти определитель системы (матрицы А);

2) найти матрицу 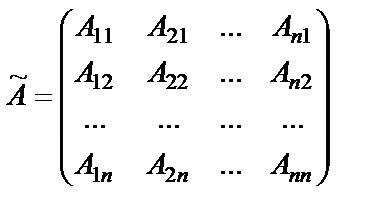, союзную для матрицы А, где 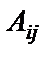- алгебраические дополнения всех элементов определителя системы;

3) найти матрицу 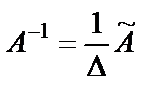, обратную матрице А;

4) умножить матрицу 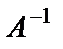на матрицу-столбец В: .

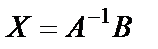Пример 2. Решить систему уравнений 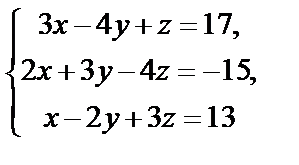матричным методом.

Решение. Обозначим 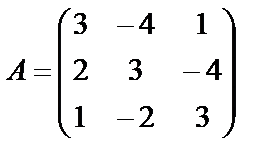, , 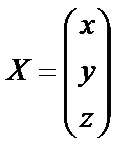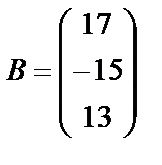. Тогда систему уравнений можно записать в виде матричного уравнения 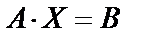. Вычислим определитель матрицы А :

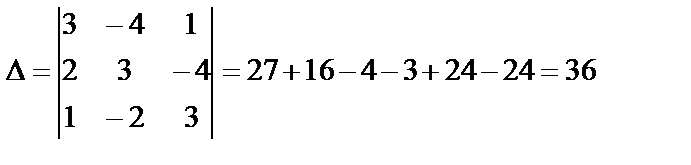. Так как определитель матрицы А отличен от нуля, то для неё существует обратная матрица 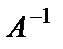и система имеет единственное решение.

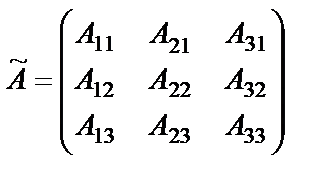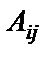
Найдём матрицу , где алгебраические дополнения элементов определителя : , , ,

, , ,

, ,

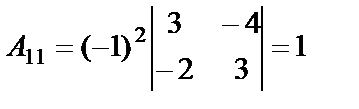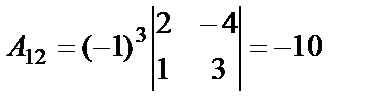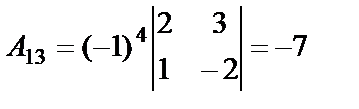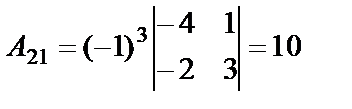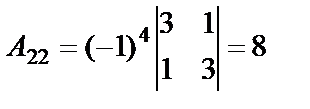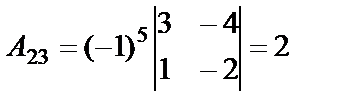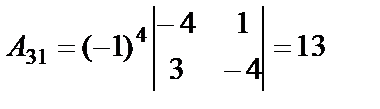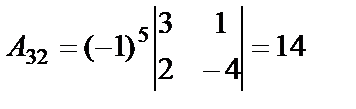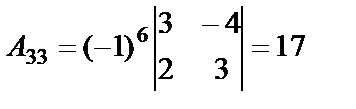. Получили 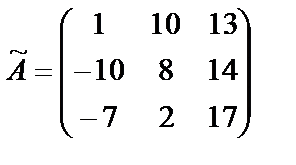. Тогда

= .

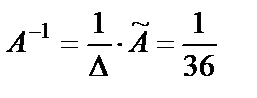
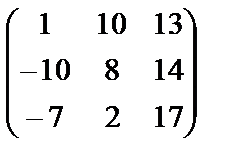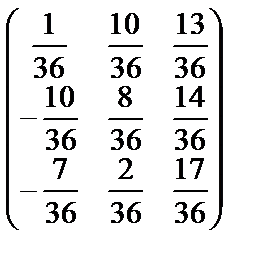Найдём решение системы : 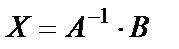или

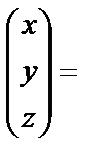
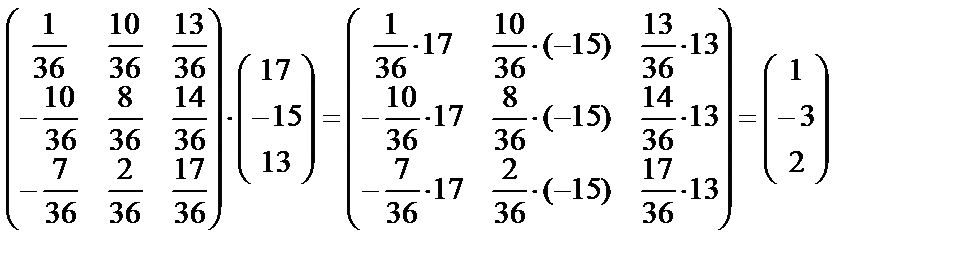. Таким образом, , .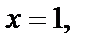

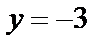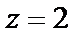Вопросы для самоконтроля знаний

1) Какая матрица называется обратной для данной матрицы и при каких условиях она существует?

2) Какая матрица называется союзной для данной матрицы?

3) Как находится обратная матрица?

4) Как можно записать систему линейных уравнений в матричной форме?

5) Как находится решение системы линейных уравнений, записанной в матричной форме?