C. события В при условии, что событие А состоялось

D. совместного появления независимых событий.

E. события В при условии, что оно входит в полную группу событий.

З А Д А Н И Е № 20

Выберите правильное продолжение формулировки теоремы: "Вероятность

появления одного из нескольких несовместных событий (А или В) равна":

A.Произведению их вероятностей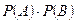

B. Сумме их вероятностей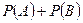

C. Разности их вероятностей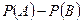

D. Произведению вероятности первого события на условную вероятность второго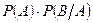

E. Сумме вероятностей первого события и условной вероятности второго P(A) + P(B/A).

З А Д А Н И Е № 21

Когда применяется теорема сложения вероятностей ?

A. Когда необходимо рассчитать вероятность одновременного появления нескольких зависимых событий;

B. Когда необходимо рассчитать вероятность одновременного появления нескольких независимых событий;

C. Когда необходимо рассчитать вероятность появления какого-либо события из группы благоприятствующих опыту несовместных событий;

D. Когда необходимо рассчитать вероятность появления какого-либо зависимого события.

З А Д А Н И Е № 22

Выберите правильную формулировку теоремы умножения вероятностей для независимых событий.

A. Вероятность появление одного из двух или более независимых событий равна произведению вероятностей этих событий;

B. Вероятность одновременного появления в результате опыта двух и более независимых событий равна произведению вероятностей этих событий;

C. Вероятность появления в результате опыта двух событий равна произведению вероятности одного события на условную вероятность другого события.

D. Вероятность одновременного появления в результате опыта двух и более независимых событий равна произведению условных вероятностей этих событий.

З А Д А Н И Е № 23

Выберите правильное продолжение формулировки теоремы :"Вероятность сложного события, состоящего из совпадения двух независимых простых событий А и В равна:

A. произведению их вероятностей ;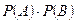

B. сумме их вероятностей ;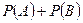

C. единице.

D. произведению вероятности первого события на условную вероятность второго события ;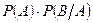

E. сумме вероятностей первого события и условной вероятности второго события ;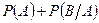

З А Д А Н И Е № 24

Теорема умножения для независимых событий применяется в том случае, когда требуется вычислить

A. вероятность одновременно появления нескольких зависимых событий;

B. вероятность одновременного появления нескольких независимых событий;

C. вероятность появления какого-либо события из группы благоприятствующих опыту несовместных событий

D. вероятность появления одного независимого события.

З А Д А Н И Е № 25

Выберите правильную формулировку теоремы умножения вероятностей для зависимых событий.

A. Вероятность появления одного из двух или более зависимых событий равна произведению условных вероятностей этих событий;

B. Вероятность совместного появления в результате опыта двух (или более) зависимых событий равна произведению вероятности первого события на условную вероятность второго (третьего и т.д.).

C. Вероятность появления в результате опыта двух и более зависимых событий равна произведению вероятностей этих событий.

D. Вероятность появления одного из двух или более зависимых событий равна сумме условных вероятностей этих событий.

E. Вероятность появления в результате опыта двух и более зависимых событий равна сумме вероятностей этих событий.

З А Д А Н И Е № 26

Когда применяется теорема умножения для зависимых событий?