Фундаментальные противоречия в основаниях классической механики
В начале XX в. на смену классической механике пришла новая фундаментальная теория — специальная теория относительности (СТО). Созданная усилиями ряда ученых, прежде всего А. Эйнштейном, она позволила непротиворечиво объяснить многие физические явления, которые не укладывались в рамки классических представлений. В первую очередь это касалось закономерностей электромагнитных явлений в движущихся телах.
Создание теории электромагнитного поля и экспериментальное доказательство его реальности поставили перед физиками задачу выяснить, распространяется ли принцип относительности движения (сформулированный еще Галилеем), справедливый для механических явлений, на явления, присущие электромагнитному полю. Во всех инерциальных системах (т.е. движущихся прямолинейно и равномерно друг по отношению к другу) применимы одни и те же законы механики. Но справедлив ли принцип, установленный для механических движений материальных объектов, для немеханических явлений, особенно тех, которые представлены полевой формой материи, в частности электромагнитных явлений?
Ответ на этот вопрос требовал изучения закономерностей взаимосвязи движущихся тел с эфиром, но не как с механической средой, а как со средой — носителем электромагнитных колебаний. Отдаленные истоки такого рода исследований складывались еще в XVIII в. в оптике движущихся тел. Впервые вопрос о влиянии движения источников света и приемников, регистрирующих световые сигналы, на оптические явления возник в связи с открытием аберрации света английским астрономом Брадлеем в 1728 г. (см. 7.1). Данный вопрос применительно к волновой теории света был значительно более сложным, чем для теории, основанной на представлении о корпускулярной природе света. Его решение требовало введения ряда гипотетических допущений относительно явлений, которые очень сложно выявить в опыте: как взаимодействуют весомые тела и эфир (полагали, что эфир проникает в тела); отличается ли эфир внутри тел от эфира, находящегося вне их, а если отличается, то чем; как ведет себя эфир внутри тел при их движении, и т.д. В физике сложилось три различных интерпретации характера взаимодействия вещества и эфира.
Возрождавший волновую теорию света в начале XIX в. Т. Юнг, касаясь вопросов оптики движущихся тел, отметил, что явление аберрации света может быть объяснено волновой теорией света, если предположить, что эфир повсюду, в том числе и внутри движущихся тел, остается неподвижным. В этом случае явление аберрации объясняется, как и в корпускулярной теории света.
В 1846 г. английский физик Дж. Г. Стокс разработал новую теорию аберрации, основанную на аналогиях с гидродинамикой. Он исходил из предположения, что Земля при своем движении полностью увлекает окружающий ее эфир и скорость эфира на поверхности Земли в точности равна ее скорости. Но последующие слои эфира движутся все медленнее и медленнее, и это обстоятельство и вызывает искривление волнового фронта, что и воспринимается как аберрация. Из этой теории следует, что в любых оптических опытах, проведенных на Земле, не может быть обнаружена скорость ее движения.
Существовала и третья точка зрения, принадлежавшая Френелю. Он предположил, что эфир частично увлекается движущимися телами. Френель показал также, что коэффициент увлечения имеет порядок (v/c)2, а значит, опытная проверка этой идеи требует очень точного эксперимента.
Сравнивая свою теорию с теорией Френеля, Стокс указывал, что эти теории хотя и основываются на противоположных гипотезах, но практически приводят к одинаковым результатам. Опыты, имевшие целью обнаружить скорость движения Земли относительно эфира, не дали положительных результатов. Они объяснялись и теорией Стокса, и теорией Френеля, поскольку их точность была недостаточной для обнаружения эффекта порядка (v/с)2.
Принципиальная сторона вопроса сводилась в сущности к двум возможным гипотетическим допущениям. Первое допущение состояло в том, что эфир полностью увлекается движущейся системой.
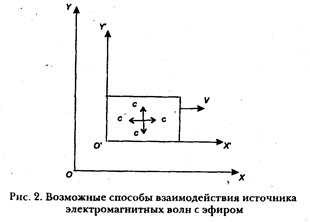
Допустим система X'Y'O' (рис. 2) с источником света (скорость света с) движется со скоростью V по отношению к неподвижной системе XYO (в условиях, когда эфир полностью увлекается движущейся системой). Тогда в соответствии с принципом относительности:
для наблюдателя в системе X'Y'O' скорость света будет одинакова и равна с;
для наблюдателя в системе XYO скорость света будет различной и равна V = с± V.
Вместе с тем ряд опытов, которые были поставлены еще в XIX в., показал, что скорость света всегда одинакова во всех системах координат независимо от того, движется ли излучающий его источник или нет, и независимо от того, как он движется. Таким образом, гипотеза о том, что эфир полностью увлекается движущейся системой позволяла придерживаться принципа относительности, но тем не менее противоречила опыту.
Второе допущение прямо противоположно первому: движущаяся система проходит через эфир, не захватывая его. Это предположение, по сути, отождествляет эфир с абсолютной системой отсчета и приводит к отказу от принципа относительности Галилея — ведь в системе координат, связанной с эфирным морем, законы природы отличаются от законов во всех других системах.
Пусть система XYO (см. рис. 2) жестко связана с эфиром, а система X'Y'O' движется по отношению к ней, а значит, и по отношению к неподвижному эфиру, со скоростью V. В таком случае:
для наблюдателя в системе XYO скорость света всегда постоянна и равна с.
для наблюдателя в системе X'Y'O' скорость света должна зависеть от скорости движения самой системы и быть равной V = с± V, где V — скорость света для наблюдателя в системе X'Y'O'.
Таким образом, только в одной системе координат, связанной с неподвижным эфирным морем, скорость света была бы одинакова во всех направлениях. В любой другой системе, движущейся относительно эфирного моря, она зависела бы от направления, в котором производилось измерение. Следовательно, для того чтобы проверить вторую гипотезу, необходимо измерить скорость света в двух противоположных направлениях. С этой целью можно воспользоваться движением Земли вокруг Солнца: тогда скорость света в направлении движения Земли будет отличаться от скорости света в противоположном направлении.
Очевидно, что если Земля не увлекает при своем движении окружающий эфир, то в одном случае эта скорость равна:
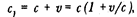
а в другом случае:
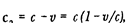
где v — скорость Земли. Таким образом, разница в скорости света в первом и втором случаях имеет первый порядок малости относительно v/c. Однако для проведения такого опыта нужно уметь измерять время, необходимое для прохождения светом известного расстояния в направлении движения Земли. Но не ясно, как эта задача может быть экспериментально разрешима.
Реальный эксперимент по определению скорости света на Земле возможен тогда, когда скорость света определяется по времени, котopoe требуется для прохождения светом расстояния в прямом и обратном направлениях. В частности, существует экспериментальная возможность сравнения времени прохождения светом определенного расстояния S туда и обратно — первый раз вдоль движения Земли, а второй раз, в направлении, перпендикулярном этому движению. Но при этом разница во времени в первом и втором случаях является величиной второго порядка относительно v/c, т.е. ~ v2/с2. Но v2/с2 чрезвычайно мало ≈ 10-8, и потому эксперимент должен быть исключительно точным. Такой эксперимент в 1887 г. был проведен А. Майкельсоном. Результаты этого эксперимента достоверно свидетельствовали, что на скорость света не влияет движение Земли, а следовательно, о несостоятельности второго допущения.
Для того чтобы «спасти» его, Дж. Фитцджеральд и независимо от него Г.А. Лоренц высказали в 1892 г. оригинальную гипотезу, согласно которой отрицательный результат опыта Майкельсона может быть объяснен тем, что размеры каждого движущегося в эфире тела при движении в эфире уменьшаются в направлении движения относительно эфира в 1/(1 – v2/c2)1/2 раз. Эта гипотеза чисто формально объясняла отрицательный результат опыта Майкельсона, не давая никаких разумных теоретических объяснений причин изменения размеров тел. Более того, из этой гипотезы следовало, что вообще отсутствуют какие-либо средства, позволяющие решить вопрос о том, движется ли тело относительно эфира или покоится.
Впоследствии было показано, что для последовательного проведения «гипотезы сокращения» необходимо также допустить, что в системе, движущейся равномерно в неподвижном эфирном море, необходима и новая мера времени, а допущение о неувлекаемом эфире будет соответствовать опыту и принципу относительности, если вместо преобразований Галилея ввести новую формальную систему преобразований, которая получила название «преобразования Лоренца»:
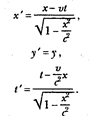
Заметим, что при скоростях системы, существенно меньших скорости света (т.е. v « с), отношение v2/с2 → 0 и тогда преобразования Лоренца превращаются в классические преобразования Галилея.
Таким образом, к рубежу XIX—XX вв. развитие физики привело к осознанию противоречий и несовместимости трех принципиальных положении классической механики:
1) скорость света в пустом пространстве всегда постоянна, независимо от движения источника или приемника света;
2) в двух системах координат, движущихся прямолинейно и равномерно друг относительно друга, все законы природы строго одинаковы, и нет никакого средства обнаружить абсолютное прямолинейное и равномерное движение (принцип относительности);
3) координаты и скорости преобразовываются из одной инерциальной системы в другую согласно классическим преобразованиям Галилея.
Было ясно, что эти три положения не могут быть объединены, поскольку они несовместимы. Долгое время усилия физиков были направлены на то, чтобы попытаться каким-либо образом изменить первые два положения, оставив неизменным третье как само собой разумеющееся. С другой стороны, каждый раз результаты опытов доказывали истинность первых двух положений. В конце концов появилась даже идея замены преобразований Галилея, но она выступила лишь в виде гипотезы ad hoc.
Внутренней логикой своего развития физика подводилась к необходимости найти нестандартный путь в разрешении этого фундаментального противоречия в ее основаниях.
