Дополнительный материал

Перечень вопросов

Введение

Механические свойства биологических тканей. Вязкоупругие, упруговязкие и вязкоупругие, упруговязкие и вязкопластичные системы. Механические свойства мыщц, костей, кровеносных сосудов, легких.

Задачи, объекты и методы биомеханики.

Значение биомеханики для медицины

Биомеханика опорно-двигательной системы человека. Биомеханические аспекты остеогенеза .

Сочленение и рычаги в опорно-двигательном аппарате человека.

Эргометрия. Механические свойства тканей организма

Тема:

Основы биомеханики

Введение

Механические процессы в живом мире протекают на разных уровнях организации, от целого организма до клетки и субклеточных структур, и относятся к числу важнейших явлений в организме. Биомеханические явления весьма разнохарактерны и включают в себя такие процессы, как функционирование опорно-двигательной системы организма, процессы деформации тканей и клеток, распространение волн упругой деформации, сокращение и расслабление мышц, конвекционное движение биологических жидкостей и легочного газа.

Момент инерции (J) материальной точки равен произведению массы (m) материальной точки на квадрат расстояния (г) этой точки от оси вращения:

J=mr²

Момент инерции твердого тела

,

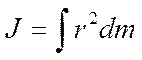где интегрирование должно проводиться по всему объему тела

Если для какого-либо тела известен его момент инерции (J₀) от­носительно оси, проходящей через центр тяжести, то момент инерции (J) относительно любой оси, параллельной первой, может быть найден по формуле

J = J₀ + mа²,

где а — расстояние от центра тяжести тела до оси вращения; m — масса тела.

Момент инерции различных однородных тел массой m относи­тельно оси, проходящей через центр масс: шара радиусом R

J= mR²2/5,

цилиндра с внутренним радиусом r и внешним R (ось враще­
ния совпадает с геометрической осью цилиндра)

J= m(r²+R²)/2

В частном случае момент инерции: тонкостенного цилиндра (R ≈ г)

J=mR²

сплошного цилиндра (г=0)

J= mR²/2;

тонкого стержня длиной l (ось вращения проходит перпенди­кулярно стержню через его середину)

J= ml²/12

Момент силы относительно оси вращения равен произведе­нию силы F на плечо l:

,

где l— кратчайшее расстояние от оси вращения до линии дейст­вия силы.

Изменение момента количества движения пропорционально величине приложенного момента силы и времени его действия (основное уравнение динамики вращательного движения):

dL = Mdt,

где dL — изменение момента количества движения.

Момент ко­личества движения L равен произведению момента инерции J на угловую скорость вращения ω_о, т. е.

L = Jω₀;

М — момент силы, приложенной к телу; dt — промежуток времени, в течение ко­торого на тело действовала сила.

Момент импульса (момент количества движения) материальной точки

L_i=m_iv_ir_i

Момент импульса тела

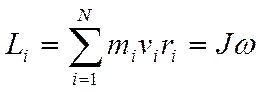
Если момент инерции тела постоянен, то основное уравне­ние динамики вращательного движения можно записать в виде

Jdω₀ = Mdt или М =Jε,

где ε — угловое ускорение.

Для изолированного тела, способного изменять момент инер­ции при вращении, закон сохранения момента количества дви­жения можно записать так:

L = const или Jω₀ = const.

Кинетическая энергия вращающегося тела

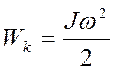
Кинетическая энергия тела, вращающегося с угловой ско­ростью ω вокруг оси, при поступательном движении оси со ско­ростью v

E_k=Jω²/2+mv²/2

Элементарная работа во вращательном движении

dA=Mdφ

где М — момент силы, приложенной к телу. Работа силы при вращательном движении

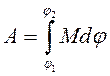
где углы φ₁ и φ₂ соответствуют начальному и конечному положе­ниям радиуса-вектора любой точки твердого тела.

Сила, действующая на частицу со стороны окружающей жидко­сти, при центрифугировании

F₁ = ρ₀Vω²r,

где ρ₀ — плотность жидкости, V — объем частицы, ω — угловая скорость вращения, r — расстояние частицы от оси вращения.

Сила, действующая на частицу при ее движении по окружности,

F = ρ₁Vω²r,

где ρ₁ — плотность вещества частицы. При F₁≠F происходит перемещение частицы в направлении к оси вращения (при F₁> >F) или от оси (при F₁<.F).