Рассмотрим основные признаки живого, его сущность.

Жизнь – это способ существования белковых тел, с присущим ему характерным обменом веществ с окружающей их внешней средой.

Современная биология при описании живого перечисляет основные свойства живых организмов. Считается, что только совокупность данных свойств дает представление о специфике жизни.

К числу свойств живого обычно относят следующие:

* Живые организмы характеризуются сложной, упорядоченной структурой. Уровень их организации значительно выше, чем в неживых системах.

* Живые организмы получают энергию из окружающей среды, используя ее на поддержание своей высокой упорядоченности. Большая часть организмов прямо или косвенно использует солнечную энергию.

* Живые организмы активно реагируют на окружающую среду. Если толкнуть камень, то он пассивно сдвигается с места. Если толкнуть животное, оно отреагирует активно: убежит, нападет или изменит форму. Способность реагировать на внешние раздражения – универсальное свойство всех живых существ, как растений, так и животных.

* Живые организмы не только изменяются, но и усложняются. Так, у растения или животного появляются новые ветви, или новые органы, отличающиеся по своему химическому составу от породивших их структур.

* Все живое размножается. Эта способность к самовоспроизведению, пожалуй, самая поразительная способность живых организмов. Причем потомство и похоже, и одновременно чем-то отличается от родителей. В этом проявляется действие механизмов наследственности и изменчивости, определяющих эволюцию всех видов живой природы.

* Сходство потомства с родителями обусловлено еще одной замечательной особенностью живых организмов – передавать потомкам заложенную в них информацию, необходимую для жизни, развития и размножения. Эта информация содержится в генах – единицах наследственности, мельчайших внутриклеточных структурах. Генетический материал определяет направление развития организма. Потомки похожи на родителей, однако информация в процессе передачи видоизменяется, искажается.

* Живые организмы хорошо приспособлены к среде обитания и соответствуют своему образу жизни. Строение живых организмов - крота, рыбы, лягушки, дождевого червя полностью соответствуют условиям, в которых они живут.

Из совокупности этих признаков вытекает следующее обобщенное определение сущности живого: жизнь есть форма существования сложных, открытых систем, способных к самоорганизации и самовоспроизведению. Важнейшими функциональными веществами этих систем являются белки и нуклеиновые кислоты.

Жизнь, по мнению Ф. Типлера, лишь некая закодированная информация, которая сохраняется естественным отбором ”. Тогда жизнь, как информация является вечной, бесконечной и бессмертной. Ценность этого определения состоит в попытке выделения из всех критериев жизни в качестве главного – способность живых организмов сохранять и передавать информацию.

Если подходить к уровням организации живого через критерий масштабности наиболее распространенными являются следующие:

* Биосферный – содержащий всю совокупность живых организмов Земли вместе с окружающей их природной средой. На этом уровне рассматривается проблема изменения концентрации углекислого газа в атмосфере, которая по расчетам ежегодно возрастает на 0,4%. Данный факт создает опасность глобального повышения температуры, резкого возрастания “парникового эффекта”.

* Уровень биогеоценозов выражает следующую ступень структуры живого, состоящую из участков Земли с определенным составом живых и неживых компонентов, представляющих единый природный комплекс, экосистему. Рациональное использование природы невозможно без знания структуры и функционирования биогеоценозов, или экосистем.

* Популяционно-видовой уровень образуется свободно скрещивающимися между собой особями одного и того же вида. Его изучение важно для выявления факторов, влияющих на численность популяции.

* Организменный и органно-тканевый уровни отражают признаки отдельных особей, их строение, физиологию, поведение, а также строение и функции органов и тканей живых существ.

* Клеточный и субклеточный уровни отражают процессы специализации клеток, а также различные внутриклеточные включения.

* Молекулярный уровень составляет предмет молекулярной биологии, одной из важнейших проблем которой является изучение механизмов передачи генной информации, развитие генной инженерии и биотехнологии.

На каждом из основных уровней организации природы имеются свои, особые “первокирпичники”. В биологии к ним относится клетка, в физике - фундаментальные частицы – кварки. В сфере химических наук место “первокирпичников” занимают более крупые частицы – молекулы и атомы различных химических элементов. Как считают с конца CIC века они делимы. Атом – более устойчивая, стабильная частица, чем кварк.

Клетка является мельчайшей системой, обладающей всем комплексом свойств живого, в том числе и носителем генетической информации – важнейшей основы эволюционного развития живого мира.

Создание клеточной теории, основы которой были заложены немецкими учеными Т. Шванном и М.Я. Шлейденом, стало одним из крупнейших достижений биологии CIC в. Основное положение клеточной теории состоит в утверждении, что все растительные и животные организмы состоят из клеток, сходных по своему строению. Это положение стало еще одним свидетельством единства происхождения и развития всех видов живого.

Многочисленные исследования в области цитологии (науке о живой клетке), показали, что все клетки имеют некоторые общие свойства не только в строении, но и в функциях. Они осуществляют обмен веществ, способны к саморегуляции своего состояния, могут передавать наследственную информацию.

Вместе с тем выяснилось, что клетки весьма многообразны. Они могут существовать как одиночные организмы (амебы), а также в составе многоклеточных. У клеток разный срок существования. Так, некоторые клетки пищевода отмирают у человека через несколько дней после появления, а срок жизни нервных клеток может совпадать с продолжительностью жизни человека. Жизненный цикл любой клетки завершается или делением и продолжением жизни, но уже в обновленном виде, либо гибелью.

Клетки образуют ткани(нервная, мышечная и т.д.), а несколько типов тканей - органы (сердце, легкие и пр.). Группы органов, связанные с решением каких-то общих задач, называют системами организма.

Клетка имеет сложную структуру. Она обособляется от внешней среды оболочкой, которая, будучи неплотной и рыхлой, обеспечивает взаимосвязь клетки с внешним миром, обмен с ней веществом, энергией и информацией. Обмен веществ, обеспечиваемый клеткам, - важнейшее свойство всего живого. Это свойство в биологической литературе называют метаболизмом клеток.

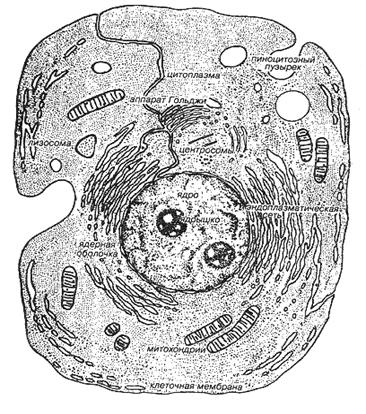Метаболизм в свою очередь служит основой для другого важнейшего свойства клетки – сохранения стабильности, устойчивости условий внутренней среды клетки. Это свойство клеток, присущее всей живой системе, называют гомеостазом. Гомеостаз - постоянство свойств клетки, поддерживается обменом веществ, или метаболизмом.

Рис.3.1. онтинентальные плиты Земли (по теории неомобилизма).

Обмен веществ – сложный, многоступенчатый процесс, включающий доставку в клетку исходных продуктов, получение из них энергии и белков, выведение из клетки в окружающую среду

выработанных полезных продуктов, энергии и “ вредных веществ”.

Следует отметить, что в последнее время к миру живого относят также и вирусы, которые не имеют клеточной структуры (бесклеточные организмы). Кроме того, существуют также некоторые организмы с клеточным строением, клетки которых не имеют типичной структуры (отсутствует ядро). Это так называемые прокариоты, безъядерные клетки. Они исторически являются предшественникам вполне развитых, имеющих ядро клеток, впервые появившихся около 3 млрд. лет тому назад – эукариотов. К прокариотам, т.е. древнейшим, безъядерным видам клеток относятся бактерии, сине–зеленые водоросли. Эти организмы имеют в своем составе нити молекул нуклеиновых кислот, которые у них, как и у всех других клеток, выполняют управленческую функцию, только они расположены не в ядре, а во внутриклеточной жидкости, в цитоплазме. Все нити управления внутриклеточным обменом находятся в особых структурах, как правило, в ядре клетки, в очень длинных цепях молекул нуклеиновых кислот (ДНК, РНК), исходной структурной единицей которых является ген. Это природное кибернетическое устройство, содержащее инструкцию, информацию, коды, определяющие характер всей деятельности клетки как по обмену веществ, так и по самовоспроизведению. Именно гены обеспечивают как важнейшие метаболические и наследственные функции клетки, так и всего организма в целом.

5.2. Принципы эволюции, воспроизводства и развития живых систем

Применительно к живой природе эволюцию понимают как образование более сложных видов из простых. Как она происходит? Существует ли целесообразность в природе? Какова роль случайности? Что является источником развития: тренировка органов (как считал Ламарк); борьба за существование и выживание наиболее приспособленных (естественный отбор, по Дарвину); способность к взаимопомощи (П.А. Кропоткин); природные катастрофы – кометы, изменения температуры и пр. (Кювье)?

Генетика опровергла представления Ламарка о наследовании приобретенных при жизни признаков с помощью очень простых опытов. Вейсман последовательно на протяжении многих поколений отрезал мышам хвосты. Он постулировал, что признаки, приобретаемые организмом и приводящие к изменению фенотипа, не оказывают прямого воздействия на половые клетки, передающие признаки следующему поколению.

Тем не менее, эволюция идет постоянно. Ч. Дарвин (1809-1882) во время своего кругосветного плавания на корабле «Бигль» собрал множество данных, свидетельствующих о том, что виды нельзя считать неизменными. После возвращения в Англию он изучает практику разведения голубей и других домашних животных, в результате чего приходит к идее естественного отбора. В 1798 г. священник Т. Мальтус в «Трактате о народонаселении», изложил свои мысли о том, к чему привел бы рост населения, если бы он ничем не сдерживался (рост средств в арифметической прогрессии и рост числа особей – в геометрической). Дарвин перенес его рассуждения на природу и обратил внимание на то, что несмотря на высокий репродуктивный потенциал, численность популяций остается относительно постоянной. Дарвин предположил, что при интенсивной конкуренции внутри популяции любые изменения, благоприятные для выживания в данных условиях, повышают способность особей размножаться и оставлять потомство.

Другим основанием теории эволюции послужил принцип униформизма английского геолога Ч. Лайеля (1797–1875), в соответствии с которым медленные ничтожные изменения приводят к поразительным результатам, если происходят долго в одном направлении. Точно так же небольшие изменения на протяжении миллионов лет приводят к образованию новых видов.

На мысль об эволюции органических форм Дарвина натолкнула находка в одном и том же регионе – в Южной Америке – скелетов ленивца – огромного (ископаемого) и маленького (современного). Он сформулировал представления о том, что основными тремя движущими силами эволюции являются – естественный отбор, наследственность, изменчивость. Естественный отбор делится на три вида – межвидовой, внутривидовой, связанный с окружающей средой.

Теория эволюции сформулирована Дарвином в 1839 г. Наибольший вклад Дарвина в науку заключался не в том, что он доказал существование эволюции, а в том, что он объяснил, как она может происходить. В 1859 г. Дарвин опубликовал труд «Происхождение видов путем естественного отбора». Гипотеза Дарвина основана на трех наблюдениях и двух выводах:

Наблюдение 1. Особи входящие в состав популяции, обладают большим репродуктивным потенциалом.

Наблюдение 2. Число особей в каждой данной популяции примерно постоянно.

Вывод 1. Многим особям не удается выжить и оставить потомство. В популяции происходит «борьба за существование».

Наблюдение 3. Во всех популяциях существует изменчивость.

Вывод 2. В «борьбе за существование» те особи, признаки которых наилучшим образом приспособлены к условиям жизни, обладают «репродуктивным преимуществом» и производят больше потомков, чем менее приспособленные особи. Этот вывод и содержит гипотезу о естественном отборе, который может служить механизмом эволюции.

Теория эволюции ознаменовала крупный прорыв в биологии, но вопросы и сомнения оставались. Всю жизнь Дарвина преследовал «кошмар» – возражение следующего содержания: если среди поля красных маков появится белый, то после скрещивания он даст розовое потомство, а через 2–3 поколения исчезнет всякое воспоминание о белом цвете. Генетика помогла дарвинизму, объяснив, что появившийся признак не может исчезнуть, так как наследственный аппарат сохраняет случайно возникшее в нем, подобно тому, как сохраняются опечатки в книгах при их воспроизводстве.

Генетика привела к новым представлениям об эволюции, получившим название неодарвинизма, который можно определить как теорию органической эволюции путем естественного отбора признаков, детерминированных генетически. Другое общепринятое название – синтетическая, или общая, теория эволюции. Механизм эволюции стал рассматриваться как состоящий из двух частей: случайные мутации на генетическом уровне и наследование наиболее удачных с точки зрения приспособления к окружающей среде мутаций, так как их носители выживают и оставляют потомство.

Некоторые из событий, приводимых в качестве доказательства эволюционной гипотезы воспроизводимы в лаборатории, однако это не значит, что они действительно происходили в прошлом, а свидетельствует об их возможности. На многие возражения до сих пор нет ответа. Поэтому концепцию Дарвина точнее все же относить к гипотезам, которые требуют дальнейшего подтверждения.

Однако, теория Дарвина не была единственна. Так, например, русский ученый и революционер П.А. Кропоткин придерживался точки зрения, в соответствии с которой взаимопомощь (коэволюция) является более важным фактором эволюции, чем борьба.

Случайно образовавшиеся более сложные формы увеличивают разнообразие и стало быть устойчивость экосистем. Удивительная согласованность всех видов жизни есть следствие коэволюции.

Концепция коэволюции хорошо объясняет эволюцию в системе «хищник – жертва» – постоянное совершенствование и того, и другого компонента системы. В системе «паразит – хозяин» естественный отбор должен вроде бы способствовать выживанию менее вирулентных (не опасных для хозяина) паразитов и более резистентных (устойчивых к паразитам) хозяев. Постепенно паразит становится комменсалом, т.е. безопасным для хозяина, а затем они могут стать мутуалами – организмами, которые способствуют взаимному процветанию, как грибы и фотосинтезирующие бактерии, вместе образующие лишайники. Но так происходит не всегда. Паразиты являются неизбежной, обязательной частью каждой экосистемы. Коэволюционная «гонка вооружений» способствует большему разнообразию экосистем. Паразиты препятствуют уничтожению хозяевами других видов.

5.3. Физика колебаний, волновые явления. Циклические процессы жизнедеятельности как колебательный

процесс

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природе.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса).

Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа

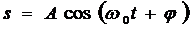, (5.1)

где: А - максимальное значение колеблющейся величины, называемое амплитудой колебания, 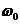- круговая (циклическая) частота, 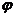-начальная фаза колебаний в момент времени t=0, ( 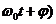- фаза колебаний в момент времени t. Фаза колебаний определяет значение колеблющейся величины в данный момент времени. Фаза колебаний определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то s может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебаний, за который фаза получает приращение 2 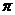, т.е

;

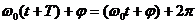откуда Т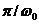=2 (5.2)

Величина, обратная периоду колебаний,

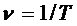, (5.3)

т.е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (5.2) и (5.3), получим

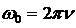
Единица частоты - герц (Гц): 1 Гц- частота периодического процесса, при котором за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:

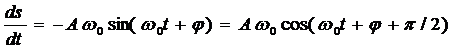; (5.4)

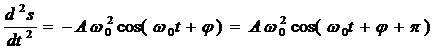, (5.5)

т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (5.4) и (5.5) соответственно равны 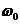А и А 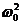. Фаза величины (5.4) отличается от фазы (5.1) на 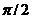, а фаза величины (5.5) отличается от фазы (5.1) на 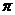. Следовательно, в моменты времени, когда s=0, ds/dt приобретает максимальное положительное значение (рис.5.1).

Из выражения (5.5) можно получить дифференциальное уравнение гармонических колебаний:

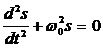(5.6)

Решением этого уравнения является выражение (12.1), т.е.

s=А cos ( + ).

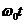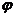механические гармонические колебания

Пусть материальная точка совершает гармонические колебания вдоль оси х около положения равновесия, принятого за начало координат. Тогда зависимость х от времени t задается уравнением, аналогичным уравнению (5.1):

х = A cos ( 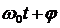), (5.7)

Согласно выражениям (5.4) и (5.5), скорость 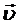и ускорение 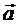колеблющейся точки соответственно равны

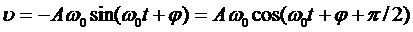(5.8)

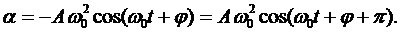
Сила 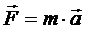, действующая на колеблющуюся материальную точку массой m, с учетом (5.7) и (5.8) равна

F = - m 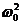х

Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).

Кинетическая энергия материальной точки, совершающей прямо-линейные гармонические колебания, равна:

Т= 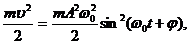(5.9)

или Т= 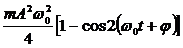(5.10)

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна

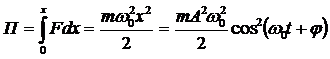, (5.11)

или 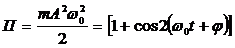(12.12)

Сложив (5.9) и (5.11), получим формулу для полной энергии:

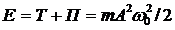(5.13)

Так как амплитуда и частота колебаний есть постоянные величины (для незатухающих колебаний), из последнего выражения видно, что энергия колебательной системы остается постоянной с течением времени.

Наглядными моделями колебательных механических систем являются пружинный, и математический маятники. Они оба - гармонические осцилляторы, колебания которых описываются уравнением вида:

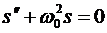(5.14)

Пружинный маятник-это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F= - kx, где k-жескость пружины. Уравнение движения такого маятника 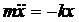, или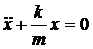

Из выражений (3.14) и (3.1) следует , что пружинный маятник совершает гармонические колебания по закону х = А 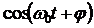с циклической частотой

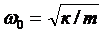(5.15)

и периодом 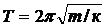(5.16)

Формула (5.15) справедлива для упругих колебаний в пределах выполнения закона Гука, т.е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (5.11) и (5.15), равна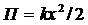

Математический маятник- это идеализированная система, состоящая из материальной точки массой m , подвешенной на длинной, тонкой, нерастяжимой, невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.

Момент инерции математического маятника

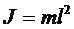, (5.17)

где: l- длина маятника.

Предположив, что математический маятник это частный случай физического маятника, с массой, сосредоточенной в центре тяжести тела, можно получить выражение для периода малых колебаний математического маятника.

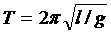(5.18)

Волновые процессы. Продольные и поперечные волны.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передается лишь состояние колебательного движения и его энергия. Поэтому, основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Среди разнообразия волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения волны.

Расстояние между ближайшими частицами, колеблющимся в одинаковой фазе, называется длиной волны 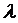. Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебаний за период, т.е.

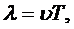
или учитывая, что Т =1/ 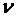, где 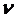- частота колебаний,

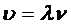
Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н.А. Умова (1846-1915), решившего задачу о распространении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.

Пример схематичного движения электромагнитной волны представлен на рис. 3.2. На нём видно, что волновой вектор (как и вектор скорости волны) направлен вдоль оси абсцисс, а вдоль Y и Z ко-леблются вектора напряжённос-ти электрического ( 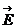) и магнит-ного ( ) 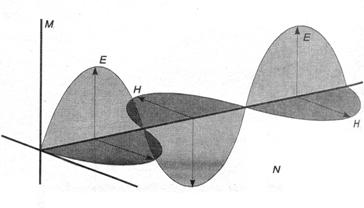полей.

Рис. 3.2. Схема распространения электромагнитной волны.

Для вывода уравнения бегущей волны - зависимости смещения колеблющейся частицы от координат и времени - рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны. В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение 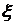будет зависеть только от координаты х и t, т.е. 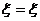(х, t). Для некоторой точки среды, находящейся на расстоянии х от источника колебаний, их уравнение запишется выражением

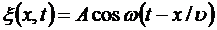(5.19)

где: 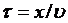, а 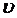- скорость распространения волны.

Следовательно, 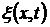является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (5.19) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то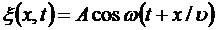

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

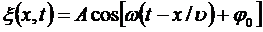, (5.20)

где: А = const- амплитуда волны, 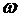- циклическая частота, 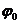- начальная фаза волны, определяемая в общем случае выбором начал отсчета x и t, 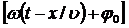- фаза плоской волны.

Для характеристики волн используется волновое число

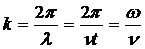(5.21)

Учитывая (5.20), уравнению (5.21) можно придать вид

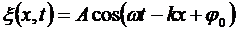(5.22)

Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (5.22) только знаком члена kx.

Если среда, в которой распространяется одновременно несколько волн, линейна, т.е. ее свойства не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения) волн: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.

Исходя из принципа суперпозиции и разложения Фурье любая волна может быть представлена в виде суммы гармонических волн, т.е. в виде волнового пакета, или группы волн. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.

В том случае, если волна распространяется в среде, её скорость определяется значениями скорости распространения. Обычно, чем выше

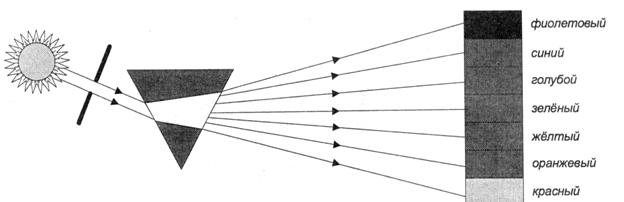
Рис. 3.3. Наблюдение дисперсии света с помощью призмы.

скорость света в среде, тем больше длина волны в ней. За счёт зависимости коэффициента преломления света от длины волны на границе прозрачных сред наблюдается явление дисперсии (“разложения” белого света в спектр). Пример дисперсии света представлен на рис.3.3. Попадая на призму белый свет, состоящий из набора семи основных монохроматических цветов, преломляется. Так как длины волн отдельных цветов различны, разные значения имеют и коэффициенты преломления. Следовательно, на экране наблюдается дисперсионный спектр.

Наиболее наглядно волновые процессы можно наблюдать на звуковых волнах. Звуковыми (или акустическими) волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16 - 20 000 Гц. Волны указанных частот воздействуя на слуховой аппарат человека, вызывают ощущение звука. Волны с n < 16 Гц (инфразвуковые) и n > 20 кГц (ультразвуковые) органами слуха человека не воспринимаются.

Совершая колебания, тело вызывает колебания прилегающих к нему частиц среды с такой же частотой. Состояние колебательного движения последовательно передается к все более удаленным от тела частицам, т.е. в среде распространяется волна с частотой колебаний, равной частоте колебаний источника, и с определенной скоростью, зависящей от плотности и упругих свойств среды. Скорость распространения звуковых волн в газах вычисляется по формуле

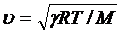(5.23)

где: R – молярная газовая постоянная, M- молярная масса, 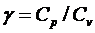- отношение молярных теплоемкостей газа при постоянных давлении и обьеме, Т –термодинамическая температура. Из формулы (3.23) вытекает, что скорость звука в газе не зависит от давления р газа, но возрастает с повышением температуры. Чем больше молярная масса газа, тем меньше в нем скорость звука. Например, при Т =273 К скорость звука в воздухе (М =29 × 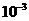кг/моль) 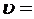331 м/с, в водороде ( 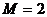× 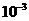кг/моль), 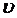= 1260 м/с.

При распространении звука в атмосфере необходимо учитывать целый ряд факторов: скорость и направление ветра, влажность воздуха, молекулярную структуру газовой среды, явление преломления и отражения звука на границе двух сред.

Эффект Доплера.

Если источник и приемник движутся относительно друг друга, частота колебаний, воспринимаемых приемником может быть определена из выражения: 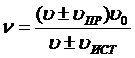, (5.24)

причем верхний знак берется, если источник и приемник сближаются, нижний знак - в случае их взаимного удаления.

Ультразвук и его применение.

Ультразвуки широко используются в технике, например для направленной подводной сигнализации, обнаружения подводных предметов и определения глубин ( гидролокатор, эхолот). Например, в эхолоте от пьезокварцевого генератора, укрепленного на судне, посылают направленные ультразвуковые сигналы, которые, достигнув дна, отражаются от неге и возвращаются обратно. Зная скорость распространения в воде и определяя время прохождения (от подачи до возвращения) ультразвукового сигнала, можно вычислить глубину. Прием эха также производится с помощью пьезокварца. Звуковые колебания, дойдя до пьезокварца, вызывают в нем упругие колебания, в результате чего на противоположных поверхностях кварца возникают электрические заряды, которые измеряются.

Получение электромагнитных волн.

Существование электромагнитных волн - переменного электромагнит-ного поля, распространяющегося в пространстве с конечной скоростью,- вытекает из уравнений Максвелла. Уравнение Максвелла сформулированы в 1865г. на основе обобщения эмпирических законов электрических и магнитных явлений. Как уже указывалось, решающую роль для утверждения максвелловской теории сыграли опыты Герца (1888), доказавшие, что электрические и магнитные поля действительно распространяются в виде волн, поведение которых полностью описывается уравнениями Максвелла.

Источником электромагнитных волн в действительности может быть любой электрический колебательный контур или проводник, по которому течет переменный электрический ток, так как для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле (ток смещения) или соответственно переменное магнитное поле. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объем пространства, в котором переменное электромагнитное поле создается. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры, а так как в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное - внутри катушки индуктивности.

Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а так же раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контору (вибратору Герца), представляющему собой два стержня, разделенных искровым промежутком. Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри конденсатора, то в открытом оно заполняет окружающее контур пространство, что существенно повышает интенсивность электромагнитного излучения. Колебания в такой системе поддерживается за счет источника .э.д.с, подключенного к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки.

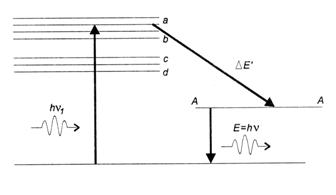На рис. 3.4 представлена схема работы твердотельного лазера. Рассматриваемый материал является типичным примером трёхуровневой квантовой систе-мы. За счёт наличия дискретных энергетических уровней и разных времён жизни на них элемен-тарных частиц, возможно накоп-ление энергии и экспрессное её высвобождение (в виде электро-магнитного импульса).

Рис. 3.4. Схема работы лазера.

Циклические процессы жизнедеятельности, как колебательный процесс

Жизнедеятельность практически всех организмов подчиняется цикличности. Наиболее просто данный факт можно наблюдать на примере суточных изменений на Земле. За 24 часа Земля поворачивается на 360⁰ вокруг своей оси. При этом наблюдается последовательная смена утра, дня, веч