Уравнения Максвелла для электромагнитного поля

Теория Максвелла представляет собой феноменологическую теорию электромагнитного поля. В ней не рассматриваются молекулярное строение среды и внутренние механизмы процессов, происходящих в среде в электромагнитном поле. Электрические и магнитные свойства среды характеризуются тремя величинами: диэлектрической проницаемостью e, магнитной проницаемостью m и удельной электрической проводимостью s.

Теория Максвелла – макроскопическая теория. В ней рассматриваются макроскопические поля макроскопических зарядов и токов, т. е. таких систем покоящихся и движущихся зарядов, пространственная протяженность которых намного больше размеров атомов и молекул.

В основе теории лежат четыре уравнения, которые могут быть представлены в двух формах: интегральной и дифференциальной. Полную систему уравнений Максвелла в интегральной форме составляют приведенные ниже уравнения (10.7.1) – (10.7.4).

Первое уравнение является обобщением закона электромагнитной индукции. Оно имеет следующий вид

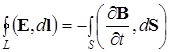. (10.8.1)

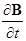Это уравнение означает, что циркуляция напряженности E электрического поля по произвольному замкнутому контуру L , мысленно проведенному в электромагнитном поле, равна взятому с обратным знаком потоку вектора через поверхность S, ограниченную этим контуром. Иными словами с переменным магнитным полем связано индуцированное вихревое электрическое поле. Причем это электрическое поле существует, не зависимо от того, находится в нем проводник или нет.

Второе уравнение Максвелла

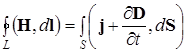(10.7.2)

означает, что циркуляция напряженности H магнитного поля по произвольному неподвижному замкнутому контуру L, мысленно проведенному в электромагнитном поле, равна полному току через поверхность S, ограниченную этим контуром. Полный ток равен сумме тока проводимости 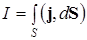и тока смещения

.

Из этого уравнения следует, что даже в отсутствие тока электрических зарядов возникает индуцированное магнитное поле, связанное с переменным электрическим полем.

Третье уравнение является обобщением электростатической теоремы Гаусса. Оно имеет вид

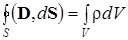, (10.7.3)

где r – объемная плотность свободных зарядов.

Это уравнение означает, что поток электрической индукции (электрического смещения) D через произвольную неподвижную замкнутую поверхность S, мысленно проведенную в электромагнитном поле, равен суммарному свободному заряду в объеме V, ограниченном этой поверхностью.

Четвертое уравнение

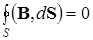(10.7.4)

означает, что поток магнитной индукции B, через произвольную неподвижную замкнутую поверхность S, мысленно проведенную в электромагнитном поле, равен нулю.

Величины, входящие в уравнения Максвелла, связаны дополнительными соотношениями (материальными уравнениями),которые учитывают реакцию среды на электромагнитное поле. Для изотропной не сегнетоэлектрической и не ферромагнитной среды эти уравнения имеют вид

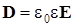; (10.7.5)

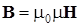; (10.7.6)

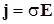. (10.7.7)

можно представить полную систему уравнений Максвелла в дифференциальной (локальной) форме:

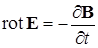; (10.7.8)

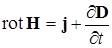; (10.7.9)

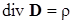; (10.7.10)

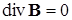. (10.7.11)

При заданных значениях e, m, s и известных E(x,y,z) и H(x,y,z) в начальный момент времени t=0 система дифференциальных уравнений Максвелла (10.7.8) – (10.7.11) имеет единственное решение.

Если электрическое и магнитное поля стационарны, т.е. ,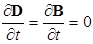

то, как следует из уравнений (10.7.8) – (10.7.11), эти поля существуют независимо друг

от друга. В этом случае электрическое поле описывается двумя основными уравнениями электростатики:

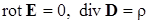. (10.7.12)

Соответственно магнитное поле описывается двумя основными уравнениями магнитостатики:

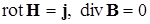. (10.7.13)

Из теории Максвелла вытекает ряд важных выводов:

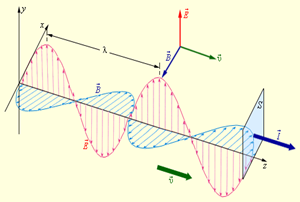1. Существуют электромагнитные волны, то есть распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы Е и В перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 10.9.1).

Рисунок 10.9.1. Синусоидальная (гармоническая) электромагнитная волна. Векторы Е,В и v взаимно перпендикулярны.

Электромагнитная волна называется монохроматической, если ее векторы Е и В совершают гармонические колебания постоянной одинаковой частоты, называемой частотой волны. Уравнение плоской монохроматической волны (рис.10.9.1) распространяющейся вдоль оси Оz (колебания векторов Е и В происходят соответственно вдоль осей Oy и Ox):

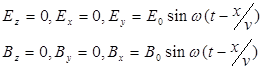
где Е и В – амплитуды напряженности электрического и индукции магнитного полей в электромагнитной волне, w - циклическая частота колебаний векторов Е и В, v – скорость распространения волны.

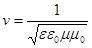2. Электромагнитные волны распространяются в веществе с конечной скоростью:

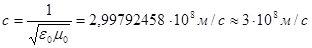Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м.

Скорость электромагнитных волн в вакууме (ε = μ = 1):

Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.

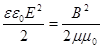3. В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: w_э = w_м.

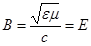Отсюда следует, что в электромагнитной волне модули индукции магнитного поля В и напряженности электрического поля Е в каждой точке пространства связаны соотношением

4. Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 10.9.1), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔW_эм, равная ΔW_эм = (w_э + w_м)υSΔt.

Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади: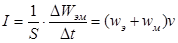

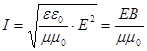Подставляя сюда выражения для w_э, w_м и υ, можно получить:

Поток энергии в электромагнитной волне можно задавать с помощью вектора I направление которого совпадает с направлением распространения волны, а модуль равен EB / μμ₀. Этот вектор называют вектором Пойнтинга (1885 г.).

В синусоидальной (гармонической) волне в вакууме среднее значение I_ср плотности потока электромагнитной энергии равно

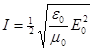
где E₀ – амплитуда колебаний напряженности электрического поля.

Плотность потока энергии в СИ измеряется в ваттах на квадратный метр (Вт/м²).

Магнитотерапия

Магнитотерапия – метод физиотерапии, в основе которого лежит действие на организм постоянного или переменного поля.

Магнитные поля по направлению силовых линий могут быть постоянными переменными, и генерироваться в непрерывном или прерывистом (импульсном) режимах с различной частотой, формой и длительностью импульсов. Магнитное поле, возникающее между полюсами магнита, может быть однородным и неоднородным.

Экспериментально установлено, что низкочастотные и постоянные магнитные поля вызывают физико-химические изменения в биологических тканях, проявляющиеся ориентацией макромолекул ферментных белков по направлению силовых линий магниттного поля, повышением проницаемости клеточных мембран, ускорением окислительно-восстановительных реакций, усилением ферментативной активности, микроциркуляции в тканях. К магнитным полям наиболее чувствительна ЦНС, особенно кора больших полушарий, гипоталамическая область, в которых отмечена активизация метаболизма.

Под действием магнита у больных гипертонической болезнью может снижаться АД, урежаться пульс. Магнитные поля могут оказывать противовоспалительное и обезболивающее действие, уменьшая отек в тканях изменяя электролитный обмен. Под их воздействием снижается активность процессов свертывания крови, улучшается регенерация тканей.

Литература.

1. Волобуев А.Н. Курс медицинской и биологической физики. М., 2002.

2. Ливенцев Н.М. Курс физики. М., 1983.

3. Ремизов А.Н. Курс медицинской и биологической физики. М., 1987.