Концепции и методологические принципы квантовой механики. Понятие квантового микросостояния
Крушение классической физики и как следствие классического естествознания связано прежде всего со знаменитым немецким физиком-теоретиком Максом Планком, который связал хаотичность электромагнитного (светового) излучения атомных осцилляторов с их дискретностью и выдвинул идею квантового излучения энергии каждым осциллятором пропорционально частоте колебаний. Планк ввел коэффициент пропорциональности, новую фундаментальную константу 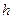 , имеющую размерность действия (энергия, умноженная на время), получившую название постоянной Планка:
, имеющую размерность действия (энергия, умноженная на время), получившую название постоянной Планка:
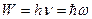 , где
, где 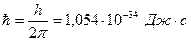 .
.
Квантовая гипотеза М. Планка сняла проблему «ультрафиолетовой катастрофы» теплового излучения, согласно которой, исходя из классических представлений о тепловом излучении, энергия излучения любого тела при любой температуре должна быть абсурдно бесконечной. А. Эйнштейн первым подхватил идею М. Планка, предположив, что электромагнитные волны не только излучаются, но и поглощаются квантами. Эта гипотеза позволила ему на основе формулы Планка и закона сохранения энергии получить в 1905 г. уравнение для внешнего фотоэффекта, подтвержденное в дальнейшем экспериментально рядом ученых и позволившее экспериментально определить постоянную Планка. Когда же было экспериментально продемонстрировано, что и процесс распространения света имеет квантовый характер (опыты В. Боте. Г. Гейгера, А. Комптона), стало ясно, что свет имеет двойственную корпускулярно-волновую природу. Так, свет при интерференции, дифракции, поляризации проявляет чисто волновые свойства, а при излучении нагретых тел, люминесценции, внешнем фотоэффекте, фотопроводимости – чисто корпускулярные свойства, т.е. как поток «частиц» (квантов), которые назвали фотонами.
Боровская теория водородоподобного атома, в основу которой Н. Бор в 1913 г. закладывает идею о квантовании величины действия при движении электрона по круговой орбите («планетарная модель атома Резерфорда-Бора»), подкрепляла возникший корпускулярно-волновой дуализм света.
И совершенно «безумная», но «революционная» в «драме идей» становления квантовой механики гипотеза была выдвинута Луи де Бройлем о том, что с двигающимся электроном связана некая волна, длина волны 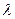 которой равна
которой равна 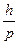 , где
, где 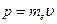 - импульс электрона. Он применил эту идею к интерпретации стационарных орбит боровской модели атома. Он считал, что в длине такой орбиты укладывается целое число длин волн электрона, и тогда волны электрона находятся в фазе сами с собой и не разрушаются собственной интерференцией. В 1924 г. де Бройль изложил эту идею в своей диссертации «Исследования по квантовой теории», которую поддержал А. Эйнштейн. Последний рекомендовал эту работу Эрвину Шредингеру, который на основе этой идеи создал одно из основных направлений квантовой механики – волновую механику.
- импульс электрона. Он применил эту идею к интерпретации стационарных орбит боровской модели атома. Он считал, что в длине такой орбиты укладывается целое число длин волн электрона, и тогда волны электрона находятся в фазе сами с собой и не разрушаются собственной интерференцией. В 1924 г. де Бройль изложил эту идею в своей диссертации «Исследования по квантовой теории», которую поддержал А. Эйнштейн. Последний рекомендовал эту работу Эрвину Шредингеру, который на основе этой идеи создал одно из основных направлений квантовой механики – волновую механику.
В 1927 г. эксперименты Дэвиссона и Джермера подтвердили «безумную» идею де Бройля в опытах по наблюдению дифракции электронов от кристалла никеля. В том же 1927 г. Дж. П. Томсон наблюдал дифракцию быстрых электронов на очень тонкой металлической фольге, изготовленной из поликристаллического материала с хаотическим расположением кристаллических осей.
В настоящее время корпускулярно-волновой дуализм распространяется на все элементарные частицы, а следовательно на все исходные принципы квантовой механики и их применения к материи, движению и фундаментальным взаимодействиям.
Эти исходные принципы квантовой механики в сжатой форме сформулировал Р. Фейнман в своих знаменитых лекциях по физике на основе рассмотрения прохождения щели электронами(см. рис. 5.1). Мы объединили в одном рисунке интерференцию электронных волн (б) со световым наблюдением за электронами (в). 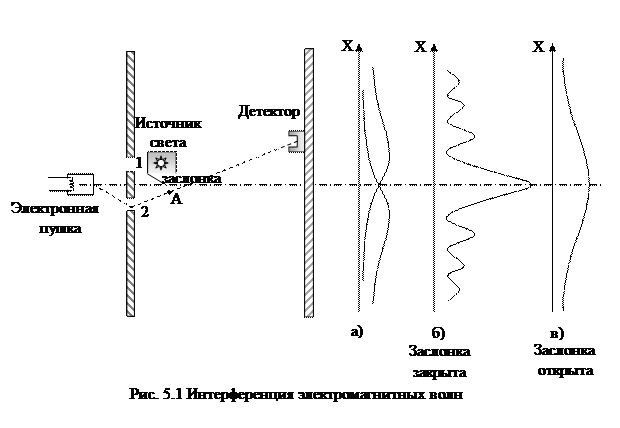
Теперь попробуем в сжатой форме прокомментировать результаты эксперимента на нашем электронном приборе. При этом мы изложим, следуя Р. Фейнмана, результаты в такой форме, чтобы они имели силу для всего класса аналогичных экспериментов. Для этого сформулируем определение идеального эксперимента: «Идеальным называется такой эксперимент, в котором все начальные и конечные условия полностью определены».
Теперь об общих выводах, которые приведем в краткой форме:
1. Вероятность некоего события в идеальном эксперименте, например, прохождения электронов через отверстие 1 или через отверстие 2 и их измерения с помощью щелчков на детекторе, равняется квадрату абсолютного значения комплексного числа 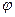 , именуемого амплитудой вероятности.
, именуемого амплитудой вероятности.
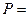 вероятность,
вероятность, 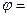 амплитуда вероятности,
амплитуда вероятности, 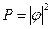 и тогда
и тогда 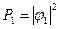 и
и 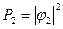 .
.
2. Если событие в эксперименте может осуществляться несколькими взаимно исключающими способами, т.е. когда, например, открыты оба отверстия (щели) и мы не фиксируем через какую щель проходит тот или иной электрон, то амплитуда вероятности для каждого отдельного события равняется сумме амплитуд вероятности для каждого отдельного способа. При этом «имеет место интерференция» (рис. 5.1, (б)).
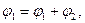
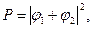 а
а 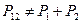 .
.
3. Если проводится эксперимент, дающий возможность определить, какой из этих двух взаимно исключающих способов осуществляется в действительности (в нашем случае контролем прохождения электронов с помощью сильного источника света), то вероятность события равна сумме вероятностей для каждого отдельного способа. Интерференция отсутствует.
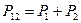 .
.
Основные идеи, принципы и законы квантово-полевой картины мира в определённой степени отражены в предыдущей лекции №3 (см. схему 21).
Мы их концептуальную основу отразим на основе выделения основополагающих концепций и методологических принципов квантовой механики (см. схему 33).
Схема 33. Основополагающие концепции и методологические принципы квантовой механики.
| v Концепция корпускулярно-волнового дуализма: «Каждый элемент материи имеет свойства волны и частицы». |
| v Концепция дискретности материи: «Всё: материя, энергия, квантовые характеристики выступают дискретными величинами, и нельзя измерить ни одну из них, не изменив её». |
| v Концепция вероятностного подхода: «Квантовая механика отказывается от стремления к точным предсказаниям того, что произойдёт при опредеоённых условиях. Мало того, это считается невозможным – единственное, что можно предсказать - это вероятность тех или иных событий. Так, что в квантовой механике мы должны удовлетвориться расчётом вероятностей, при этом считать, что такова природа на самом деле». |
v Принцип неопределённости: Принцип неопределённости в квантовой механике задаётся соотношениями неопределённостей В. Гейзенберга: 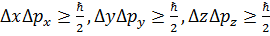 и и 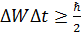 . и находит отражение в принципе дополнительности Н. Бора. . и находит отражение в принципе дополнительности Н. Бора. |
| v Принцип дополнительности: «Получение экспериментальной информации об одних физических величинах, описывающих состояние микрообъекта, неизбежно приводит к потере информации о других физических величинах, дополнительных к первым». В общенаучном плане принцип дополнительности можно сформулировать следующим образом: «Всякое истинное глубокое явление природы не может быть однозначно определено с помощью слов нашего языка и требует для своего определения по крайней мере двух взаимоисключающих дополнительных понятий». |
| v Принцип соответствия: «Любая новая более общая теория, являющаяся развитием предыдущих классических теорий, справедливость которых была экспериментально установлена для определенных групп явлений, не отвергает эти классические теории, а включает их в себя. В определенных случаях существует возможность предельного перехода новой теории в старую». |
| v Принцип простоты. «Более простая теория обычно имеет «внешнее оправдание» (соответствие эксперименту, т.е. свою верификацию) и «внутреннее совершенство» (красоту теории в виде ограничений на возможные качества систем), более «фальсифицируема и в то же время более информативна.». |
Квантовое микросостояние одной микрочастицы включает в себя как характеристики частиц, так и ее окружения. Состояние микрочастицы задается волновой функцией (амплитудой вероятности состояния) 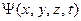 , которая является комплексной величиной, задаваемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
, которая является комплексной величиной, задаваемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
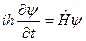 ,
,
а в случае стационарных состояний вид его упрощается
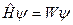 ,
,
где 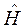 - оператор Гамильтона.
- оператор Гамильтона.
Квадрат модуля волновой функции 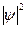 равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема,
равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема, 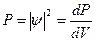 .
.
Величина плотности вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению.
Уравнение Шредингера можно применить и к квантовому микросостоянию системы частиц. Однако, в данном случае его решение всегда носит приближённый характер. При концептуальном анализе квантовой системы важную роль играют постулаты Бора (см. схему 34), квантовые статистики (см. схему 35) и квантовые числа микрочастиц (см. схему 36).
Схема 34. Обобщенные в рамках понятия квантовой системы постулаты Н. Бора.
| v Первый постулат Бора. Энергетический спектр атома (квантовой системы) дискретен. |
v Второй постулат Бора Частоты атомного излучения (электромагнитного излучения квантовой системы) связаны с энергетическими уровнями атома (квантовой системы). При переходе с уровня 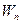 на уровень на уровень 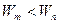 испускается квант излучения с частотой испускается квант излучения с частотой 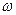 . При обратном переходе квант поглощается. . При обратном переходе квант поглощается. 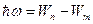 . . |
Вероятностный подход совместно с принципом тождественности, согласно которому состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц, нельзя различить ни в каком эксперименте, позволяют рассматривать такие состояния как одно физическое состояние. При этом принцип симметрии и асимметрии волновых функций при перестановке двух одинаковых микрочастиц позволяет ввести квантовые статистики Бозе-Эйнштейна и Ферми-Дирака (см. схему 35).
Схема 35. Основные свойства микрочастиц в рамках квантовых статистик.
| Название квантовой статистики | Свойства соответствующих классов микрочастиц | Тип симметрии волновой функции |
| v Статистика Ш. Бозе и А. Эйнштейна (1924 г.) | Бозоны («коллективисты» имеют тенденцию скапливаться в одном квантовом состоянии. Элементарные частицы с целочисленными спинами, например, фотоны, фононы, пионы, тяжелые промежуточные бозоны, глюоны, гравитоны. | При перестановке двух одинаковых микрочастиц знак волновой функции не меняется. Симметричные волновые функции. |
| v Статистика Э.Ферми и П. Дирака (1926 г.) | Фермионы («индивидуалисты»). Согласно принципу Паули: «Два и более одинаковых фермиона не могут находиться в одном состоянии». Элементарные частицы с получисленными спинами, например, электроны, протоны, нейтроны, кварки, все лептоны. | При перестановке двух одинаковых микрочастиц меняется знак волновой функции. Антисимметричные волновые функции |
Как видно из схемы барионная вещественная материя создается из фермионов – протонов, нейтронов и электронов. При этом особое значение, по крайней мере, в объяснении физико-химических свойств химических элементов (совокупности атомов (изотопов) с одинаковым зарядом Z ядра) приобретает электронная структура, т.е. квантовое микросостояние электронов, определяемое набором соответствующих квантовых чисел (см. схему 36).
Схема 36. Квантовые числа и соответствующие условия квантования.
| Название квантового числа и задание его значений | Условия квантования и основные характеристики |
v 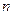 – главное квантовое число – главное квантовое число 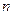 =1, 2, 3… =1, 2, 3… | Задает условие квантования энергии и характеризует уровни дискретных значений энергии атома, например, водородоподобного: 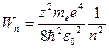 . . |
v 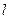 - азимутальное квантовое число - азимутальное квантовое число 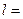 0, 1, 2, 3, …, 0, 1, 2, 3, …, 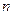 . . | Задает условие квантования момента импульса микрочастицы, например, электрона в атоме: 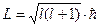 |
v 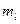 - магнитное квантовое число - магнитное квантовое число 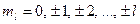 . . | Задает условие квантования проекции момента импульса микрочастицы, например, электрона в атоме: 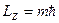 . . |
v 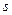 - спиновое квантовое число - спиновое квантовое число 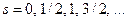 | Задает условие квантования собственного момента импульса микрочастицы, например, электрона в атоме: 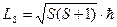 . Для электрона . Для электрона 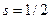 . . |
v 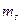 - магнитное спиновое число - магнитное спиновое число 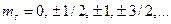 | Задает условие квантования проекции собственного момента импульса микрочастицы, например, электрона в атоме: 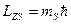 . Характеризует спиновую степень свободы электрона. Для электрона . Характеризует спиновую степень свободы электрона. Для электрона 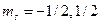 . . |
Итак, двигаясь от электромагнитной волны к понятию фотона и совершая внешне противоположное движение от электрона к его волне и наблюдению интерференции и дифракции электронов, мы осознали корпускулярно-волновой дуализм материи. Опираясь на корпускулярно-волновой дуализм и поняв вероятностный характер квантовой механики, мы ввели абстрактно-математическое описание квантового микросостояния одной микрочастицы на основе уравнения Шредингера, а также микросостояния системы тождественных частиц на основе квантовых статистик и квантовых чисел. Так мы получили новое видение электромагнитных взаимодействий и приблизились к квантовой электродинамике. Квантовая электродинамика – «это новое воззрение на взаимодействие между электронами и протонами, т.е. электромагнитная теория, но со всеми уточнениями, внесенными квантовой механикой». Как отмечает Р. Фейнман, «квантовая электродинамика – в принципе это теория всей химии, всех жизненных процессов, если жизнь сводится к химии, а, следовательно, и к физике». А так как электромагнитное взаимодействие доминирует в макромире, то «из квантовой электродинамики выводятся все известные механические, электрические и химические законы». Цивилизационная значимость квантовой механики в утилитарно-прикладном плане проявилась как в «физической экономике» индустриальной цивилизации, так и в кооперативном взаимодействии «информационной экономики» с «физической экономикой» в постиндустриальной цивилизации.
