Электронный осциллограф 7 страница

1. 1. Акустическое поле (см. § 6.3, аускультация, фонокардиография).

2. 2. Электрическое поле (см. § 12.5, электрокардиография).

3. 3. Магнитное поле (см. § 13.5, магнитокардиография).

4. 4. Электромагнитное поле (см. § 22.5, термография).

В популярной литературе часто используется термин «биопо­ле», понимая под этим некоторое специфическое влияние орга­низма на окружающие тела или некоторое специфическое излуче­ние биологических объектов. В связи с этим нужно определенно сказать, что организм является источником физических полей и каких-либо особых «биополей» не создает.

Особый вопрос — как представить результат исследования (ре­гистрации) физического поля организма (органов, тканей) для це­лей диагностики. Делается это по-разному. Так, например, при аускультации врач выслушивает звуки, т. е. субъективно оцени­вает их громкость и частоту. При электрокардиографии докумен­тально фиксируется временная зависимость разности потенциа­лов на теле пациента, возникающих при сердечной деятельности. При термографии тепловое излучение отображается на экране тепловизора.

РАЗДЕЛ 7

Физика атомов и молекул. Элементы квантовой биофизики

До конца XIX в. атом считали неделимой частицей. Однако открытие электронов и других эле­ментарных частиц убедило ученых в сложном строении атома.

Решающее значение для понимания структуры атома сыграли знаменитые опыты Резерфорда по рассеянию альфа-частиц. Были созданы условия для развития физики атома, которая изучает строение и состояние атомов и смежные вопросы. Это теория ато­ма, атомная оптическая спектроскопия, рентгеновская спектро­скопия, радиоспектроскопия и др.

Отдельные вопросы физики атомов и особенно физики молекул перекликаются с вопросами, рассматриваемыми в химии. Четкие границы раздела в этих областях науки отсутствуют.

Врач должен иметь представление о природе физических и фи­зико-химических процессов, происходящих в организме челове­ка. В конечном счете эти процессы «разыгрываются» на молекулярном уровне. Поэтому здесь рассматриваются вопросы, связан­ные с энергетическими превращениями молекул в биологических системах (хемилюминесценция, фотобиологические явления и др.). Эти темы объединяют термином «квантовая биофизика», ви­димо, по созвучию с квантовой механикой.

ГЛАВА 23

Волновые свойства частиц. Элементы квантовой механики

Квантовой механикой называют теорию, устанавливающую способ описания и законы движения микрочастиц (элемен­тарных частиц, ядер, атомов, молекул и их систем, в частности кристаллов, и т. д.)- Необычность квантово-механических представлений по сравнению с классической физи­кой инициировала пересмотр основных физических моде­лей и представлений, которые казались очевидными и незыб­лемыми. Прежде всего, это коснулось понятия самих частиц и принципов их движения.

В этой главе дается понятие не только о квантовой механике, но и о тех идеях и опытах, которые привели к этой теории. Здесь также рассматривается электронная микроскопия как метод, основанный на волновых свойствах электронов.

§ 23.1. Гипотеза де Бройля.

Опыты по дифракции электронов и других частиц

Важным этапом в создании квантовой механики явилось уста­новление волновых свойств микрочастиц. Идея о волновых свой­ствах частиц была первоначально высказана как гипотеза фран­цузским физиком Луи де Бройлем (1924)¹. Эта гипотеза появи­лась благодаря следующим предпосылкам.

В физике в течение многих лет господствовала теория, соглас­но которой свет есть электромагнитная волна. Однако после ра­бот Планка (тепловое излучение), Эйнштейна (фотоэффект) и др. стало очевидным, что свет обладает корпускулярными свойст­вами.

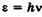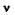Чтобы объяснить некоторые физические явления, необходимо рассматривать свет как поток частиц — фотонов. Корпускуляр­ные свойства света не отвергают, а дополняют его волновые свой­ства. Итак, фотон — элементарная частица, движущаяся со скоростью света, обладающая волновыми свойствами и име­ющая энергию , где — частота световой волны.

Логично считать, что и другие частицы — электроны, нейтро­ны также обладают волновыми свойствами.

Выражение для импульса фотона 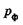получается из известной формулы Эйнштейна 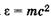и соотношений и 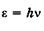_J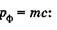

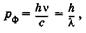(23.1)

где с — скорость света в вакууме, 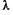— длина световой волны. Эта формула была использована де Бройлем и для других микрочас­тиц массой т, движущихся со скоростью v: 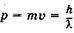, откуда

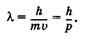(23.2)

По де Бройлю, движение частицы, например электрона, опи­сывается волновым процессом с характеристической длиной вол­ны 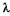, в соответствии с формулой (23.2). Эти волны называют вол­нами де Бройля.

Гипотеза де Бройля была столь необычной, что многие круп­ные физики-современники не придали ей какого-либо значения. Несколькими годами позже эта гипотеза получила эксперимен­тальное подтверждение: была обнаружена дифракция электро­нов.

Найдем зависимость длины волны электрона от ускоряющего напряжения U электрического поля, в котором он движется. Из­менение кинетической энергии электрона равно работе сил поля:

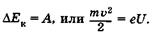
Выразим отсюда скорость v и, подставив ее в (23.2), получим

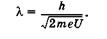(23.3)

Для получения пучка электронов с достаточной энергией, ко­торый можно зафиксировать, например, на экране осциллографа, необходимо ускоряющее напряжение порядка 1 кВ. В этом случае из (23.3) находим 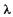= 0,4 • 10~¹⁰ м, что соответствует длине волны рентгеновского излучения.

В гл. 19 было отмечено, что дифракция рентгеновских лучей наблюдается на кристаллических телах; следовательно, для диф­ракции электронов необходимо также использовать кристаллы.

К. Дэвиссон и Л. Джермер впервые наблюдали дифракцию электронов на монокристалле никеля, Дж. П. Томсон и независи­мо от него П. С. Тартаковский — на металлической фольге (поли­кристаллическое тело). На рис. 23.1 изображена электронограм-ма — дифракционная картина, полученная от взаимодействия электронов с поликристаллической фольгой. Сравнивая этот ри­сунок с рис. 19.21, можно заметить сходство дифракции электро­нов и рентгеновских лучей.

Способностью дифрагировать обладают и другие частицы, как заряженные (протоны, ионы и др.), так и нейтральные (нейтро­ны, атомы, молекулы).

Аналогично рентгеноструктурному анализу можно применять дифракцию частиц для оценки степени упорядоченности располо­жения атомов и молекул вещества, а также для измерения пара­метров кристаллических решеток. В настоящее время широкое распространение имеют методы электронографии (дифракция электронов) и нейтронографии (дифракция нейтронов).

Может возникнуть вопрос: что происходит с отдельными час­тицами, как образуются максимумы и минимумы при дифракции отдельных частиц?

Опыты по дифракции пучков электронов очень малой интен­сивности, т. е. отдельных частиц, показали, что при этом электрон

не «размазывается» по разным направ­лениям, а ведет себя как целая частица. Однако вероятность отклонения элект­рона по отдельным направлениям в ре­зультате взаимодействия с объектом дифракции различна. Наиболее вероят­но попадание электронов в те места, ко­торые по расчету соответствуют макси­мумам дифракции, менее вероятно их попадание в места минимумов. Таким образом, волновые свойства присущи не только коллективу электронов, но и каждому электрону в отдельности.

¹ Гипотеза де Бройля была сформулирована до опытов, подтверждаю­щих волновые свойства частиц. Де Бройль об этом позднее, в 1936 г. писал так: «...не можем ли мы предположить, что и электрон так же двойстве­нен, как и свет? На первый взгляд такая идея казалась очень дерзкой. Ведь мы всегда представляли себе электрон в виде электрически заряженной материальной точки, которая подчиняется законам классической динами­ки. Электрон никогда не проявлял волновых свойств, таких, скажем, ка­кие проявляет свет в явлениях интерференции и дифракции. Попытка приписать волновые свойства электрону, когда этому нет никаких экспе­риментальных доказательств, могла выглядеть как ненаучная фантазия».

§ 23.2. Электронный микроскоп. Понятие об электронной оптике

Волновые свойства частиц можно использовать не только для дифракционного структурного анализа, но и для получения увеличенных изображений предмета.

Открытие волновых свойств электрона сделало возможным со­здание электронного микроскопа. Предел разрешения оптическо­го микроскопа (21.19) определяется в основном наименьшим зна­чением длины волны света, воспринимаемого глазом человека. Подставив в эту формулу значение длины волны де Бройля (23.3), найдем предел разрешения электронного микроскопа, в котором изображение предмета формируется электронными пучками:

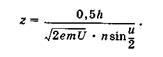(23.4)

Видно, что предел разрешения z электронного микроскопа за­висит от ускоряющего напряжения U, увеличивая которое можно добиться, чтобы предел разрешения был значительно меньше, а разрешающая способность значительно больше, чем у оптическо­го микроскопа.

Электронный микроскоп и его отдельные элементы по своему назначению подобны оптическому, поэтому воспользуемся анало­гией с оптикой для объяснения его устройства и принципа дейст­вия. Схемы обоих микроскопов изображены на рис. 23.2 (а — оп­тический; 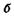— электронный).

В оптическом микроскопе носителями информации о предмете АВ являются фотоны, свет. Источником света обычно служит лампа накаливания 1. После взаимодействия с предметом (погло­щение, рассеяние, дифракция) поток фотонов преобразуется и со­держит информацию о предмете. Поток фотонов формируется с помощью линз: конденсора 3, объектива 4, окуляра 5. Изображе­ние А₁В₁ регистрируется глазом 7 (или фотопластинкой, фотолюминесцирующим экраном и т. д.).

В электронном микроскопе носителем информации об образце являются электроны, а их источником — подогреваемый катод 1. Ускорение электронов и образование пучка осуществляется фоку­сирующим электродом и анодом — системой, называемой элек­тронной пушкой 2. После взаимодействия с образцом (в основном рассеяние) поток электронов преобразуется и содержит информа­цию об образце. Формирование потока электронов происходит

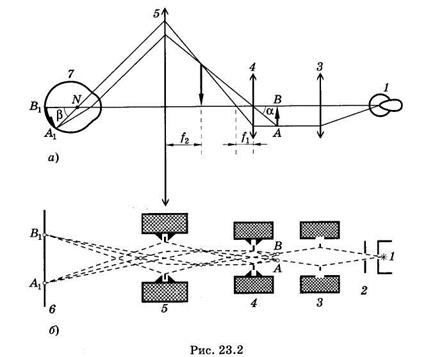
под воздействием электрического поля (система электродов и кон­денсаторов) и магнитного (система катушек с током). Эти системы называют электронными линзами по аналогии с оптическими линзами, которые формируют световой поток (3 — конденсорная; 4 — электронная, служащая объективом; 5 — проекционная). Изображение регистрируется на чувствительной к электронам фотопластинке или катодолюминесцирующем экране 6.

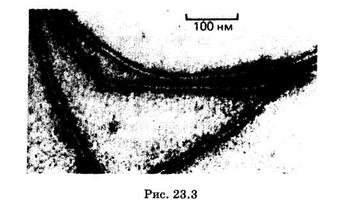
Чтобы оценить предел разрешения электронного микроскопа, подставим в формулу (23.4) ускоряющее напряжение U = 100 кВ и угловую апертуру и порядка 10~² рад (приблизительно такие уг­лы используют в электронной микроскопии). Получим 2 ~ 0,1 нм; это в сотни раз лучше, чем у оптических микроскопов. Примене­ние ускоряющего напряжения, большего 100 кВ, хотя и повыша­ет разрешающую способность, но сопряжено с техническими сложностями, в частности происходит разрушение исследуемого объекта электронами, имеющими большую скорость. Для биоло­гических тканей из-за проблем, связанных с приготовлением об­разца, а также с его возможным радиационным повреждением, предел разрешения составляет около 2 нм. Этого достаточно, чтобы увидеть отдельные молекулы. На рис. 23.3 показаны нити бел­ка фстина, имеющие диаметр примерно 6 нм. Видно, что они со­стоят из двух спирально закрученных цепей молекул белка.

Укажем некоторые особенности эксплуатации электронного микроскопа. В тех частях его, где пролетают электроны, должен быть вакуум, так как в противном случае столкновение электронов с молекулами воздуха (газа) приведет к искажению изображения. Это требование к электронной микроскопии усложняет процедуру исследования, делает аппаратуру более громоздкой и дорогой. Ва­куум искажает нативные свойства биологических объектов, а в ря­де случаев разрушает или деформирует их.

Для рассматривания в электронном микроскопе пригодны очень тонкие срезы (толщина менее 0,1 мкм), так как электроны сильно поглощаются и рассеиваются веществом.

Для исследования поверхностной геометрической структуры клеток, вирусов и других микрообъектов делают отпечаток их по­верхности на тонком слое пластмассы (реплику). Обычно предва­рительно на реплику в вакууме напыляют под скользящим (ма­лым к поверхности) углом слой сильно рассеивающего электроны тяжелого металла (например, платины), оттеняющий выступы и впадины геометрического рельефа.

К достоинствам электронного микроскопа следует отнести боль­шую разрешающую способность, позволяющую рассматривать крупные молекулы, возможность изменять при необходимости ус­коряющее напряжение и, следовательно, предел разрешения, а также сравнительно удобное управление потоком электронов с по­мощью магнитных и электрических полей.

Наличие волновых и корпускулярных свойств как у фотонов, так и у электронов и других частиц, позволяет ряд положений и

законов оптики распространить и на описание движения заря­женных частиц в электрических и магнитных полях.

Эта аналогия позволила выделить как самостоятельный раздел электронную оптику — область физики, в которой изучается структура пучков заряженных частиц, взаимодействующих с электрическими и магнитными полями. Как и обычную оптику, электронную можно подразделить на геометрическую (лучевую) и волновую (физическую).

В рамках геометрической электронной оптики возможно, в ча­стности, описание движения заряженных частиц в электриче­ском и магнитном полях, а также схематическое построение изо­бражения в электронном микроскопе (см. рис. 23.2, б).

Подход волновой электронной оптики важен в том случае, ког­да проявляются волновые свойства заряженных частиц. Хорошей иллюстрацией этому является нахождение разрешающей способ­ности (предела разрешения) электронного микроскопа, приведен­ное в начале параграфа.

§ 23.3. Волновая функция и её физический смысл

Так как с микрочастицей сопоставляют волновой процесс, ко­торый соответствует ее движению, то состояние частиц в кванто­вой механике описывается волновой функцией, зависящей от ко­ординат и времени: 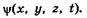Эта функция аналогична функ­ции s (см. § 5.7), описывающей волновой процесс в механике.

Если силовое поле, действующее на частицу, является стаци­онарным, т. е. не зависящим от времени, то 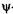-функцию можно представить в виде произведения двух сомножителей, один из ко­торых зависит от времени, а другой — от координат:

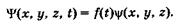(23.5)

В дальнейшем будем рассматривать только стационарные состоя­ния; y-функция координат является вероятностной характеристи­кой пространственной локализации частицы. Поясним смысл этого утверждения.

Выделим в пространстве достаточно малый объем dV = dxdydz, в пределах которого значения 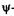функции можно считать одинако­выми. Вероятность нахождения dW_B частицы в этом объеме про­порциональна объему и определяется, согласно М. Борну, квадра­том модуля y-функции:

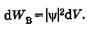(23.6)

Отсюда следует физический смысл волновой функции:

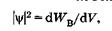(23.7)

т. е. квадрат модуля волновой функции равен плотности ве­роятности, или отношению вероятности нахождения части­цы в малом объеме dV к этому объему.

Интегрируя выражение (23.6) по некоторому объему V, нахо­дим вероятность нахождения частицы в этом объеме:

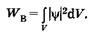(23.8)

Отсюда получаем условие нормировки волновой функции в виде 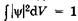, где интегрирование ведется по всему бесконечному пространству, вероятность нахождения в котором частицы равна единице.

§ 23.4. Соотношения неопределенностей

Одним из важных положений квантовой механики являются соотношения неопределенностей, предложенные В. Гейзенбергом. Существуют различные пары физических величин (называемые канонически сопряженными переменными), которые могут быть одновременно определены лишь с ограниченной точностью.

Пусть одновременно измеряют положение и импульс частицы, при этом неопределенности в измерении координаты и проекции импульса на эту координатную ось, например х, равны соответ­ственно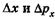

В классической физике нет каких-либо ограничений, запре­щающих с любой степенью точности одновременно измерить как одну, так и другую величину, т. е.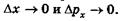

В квантовой механике положение принципиально иное: Dх и Dр_х, соответствующие одновременному определению х и р_х, связа­ны зависимостью

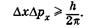(23.9)

Таким образом, чем точнее определена координата

,

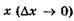тем менее точно определена соответствующая проекцияим- импульса 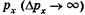, и наоборот. Аналогично для у и г:

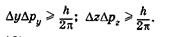(23.10)

Формулы (23.9), (23.10) называют соотношениями неопределен­ностей для координат и импульсов. Вычисления, проделанные для электрона, показывают, что его локализация внутри атомного ядра невозможна, т. к. в этом случае неопределенность его скорости должна превысить величину скорости све­та. Действительно, если 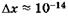м (размер ядра атома), то из (23.9) сле­дует, что величина Ap_v должна превы­сить 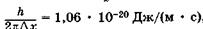, следовательно, неопределенность ско­рости 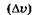электрона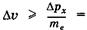 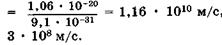, тогда как скорость света равна

Еще одной парой канонически сопряженных переменных яв­ляются энергия частицы Е и время t. Соотношение неопределен­ностей для этих переменных имеет вид

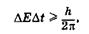(23.11)

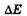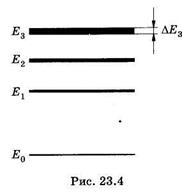
где — неопределенность энергии некоторого состояния систе­мы, 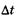— время его существования. Соотношение (23.11) означа­ет, что чем короче время существования какого-либо состояния системы, тем больше неопределенность значения энергии этого состояния. Энергетические уровни (дискретные значения энер­гии) E₁ Е₂ и т. д. имеют некоторую ширину (рис. 23.4), завися­щую от времени пребывания (времени жизни) системы в состоя­ниях, соответствующих этим уровням энергии.

«Размытость» уровней приводит к неопределенности энергии излучаемого фотона 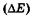и его частоты 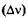при переходе системы с одного энергетического уровня на другой:

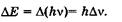(23.12)

Это экспериментально проявляется в уширении спектральных линий.

§ 23.5. Уравнение Шредингера.

Электрон в потенциальной яме

Так как состояние микрочастицы описывают 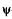-функцией, то надо указать способ нахождения этой функции с учетом внешних условий. Это возможно в результате решения основного уравнения квантовой механики, предложенного Э. Шредингером (1926). Та­кое уравнение в квантовой механике постулируется так же, как в классической механике постулируется второй закон Ньютона.

Применительно к стационарным состояниям частицы уравне­ние Шредингера может быть записано так:

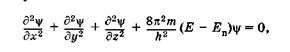(23.13)

где т — масса частицы, Е и Е_п — ее полная и потенциальная энергии (потенциальная энергия определяется силовым полем, в котором находится частица, и для стационарного случая не зави­сит от времени).

Если частица перемещается только вдоль некоторой линии, на­пример, вдоль оси ОХ (одномерный случай), то уравнение Шре­дингера существенно упрощается и принимает вид

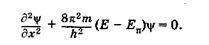(23.14)

Одним из наиболее простых примеров использования уравне­ния Шредингера является решение задачи о движении частицы в одномерной «потенциальной яме».

Пусть электрон перемещается вдоль оси ОХ только в пределах О < х < I (рис. 23.5). Это означает, что в указанном интервале y-функция отлична от нуля, а вне интервала (х < =0, х >= I) равна нулю. Так какна частицу в выделенном интервале 0 < х < I сило­вые поля не действуют, то ее потенциальная энергия может иметь любое постоянное значение (наиболее удобно принять Е_п = 0). Вне этого интервала электрона нет, т. е. электрон не может выйти за пределы интервала, поэтому в области х <= 0 и х >= I следует счи 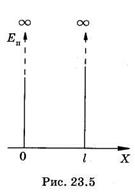тать его потенциальную энергию бесконечно большой, а волновую функцию равной нулю (y = 0). На рис. 23.5 показана графическая зависимость E_n = f(x). Интервал 0 < х < I, удовлетворяющий сформулированным вы­ше условиям, называют одномерной прямо­угольной потенциальной ямой с бесконечно высокими стенками. С учетом Е_П = 0 уравнение Шредингера (23.14) для интерва­ла 0 < х < I имеет вид

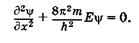(23.14а)

Произведя замену

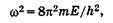(23.15)

получим

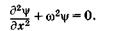(23.16)

Это уравнение аналогично дифференциальному уравнению гармони­ческого колебания (см. § 5.1), решение (5.8) которого запишем в виде

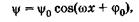(23.17)

где y₀ — амплитуда волновой функции, 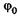— ее начальная фаза.

Чтобы найти две постоянные 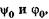а также возможные зна-

чения w или E, рассмотрим граничные условия с учетом непре­рывности волновой функции y на границах интервала:

1) 1) при х 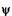= 0, =0;

2) 2) при х = I, 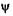= 0.

Подставляя эти значения в (23.17), получаем 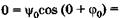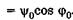, Физический смысл здесь имеет только одно значение:

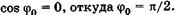
С учетом 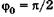из (23.17) имеем 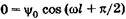. Физический смысл здесь имеет только одно значение: 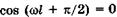, или 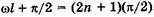, откуда

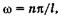(23.18)

где п — целое число, оно принимает значения 1, 2, 3, ...; п # 0, так как в противном случае 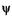= 0 при любом х, что означает отсут­ствие электрона в потенциальной яме. Число п называют кванто­вым числом. Из (23.15) находим энергию 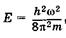, что с учетом (23. 18) дает

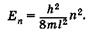(23.19)

Индекс п при Е показывает, что различным значениям квантово­го числа п соответствует и разная энергия.

Подставляя со из (23.18) в (23.17) и учитывая 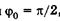, получаем

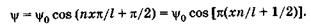(23.20)

Проанализируем выражения (23.19) и (23.20). Прежде всего при­мечательно, что решение уравнения Шредингера для электрона в потенциальной яме без каких-либо дополнительных постулатов приводит к дискретным, квантованным значениям энергии:

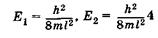и т. д.

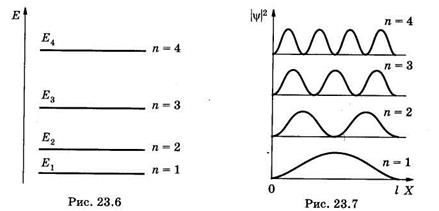
Энергетические уровни E₁ E₂, E₃, E₄, соответствующие раз­ным Состояниям электрона, схематически показаны на рис. 23.6. Вычислим разность энергий соседних уровней га + 1и га:

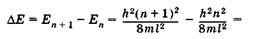
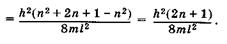(23.21)

Из (23.21) видно, что при некотором фиксированном значении га дискретность, т. е. различие энергий соседних уровней тем меньше, чем больше размеры потенциальной ямы. Так, напри­мер, рассмотри два случая при га = 1:

Возведя (23.20) в квадрат, получим плотность вероятности нахождения электрона в разных точках потенциальной ямы. 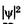На рис. 23.7 показана графическая зависимость от х при разных дискретных состояниях, т. е. разных квантовых 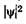числах. Как вид­но из рисунка, электрон может с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в кото-