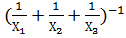Задания для самостоятельной работы. 1. Скорость потока крови в капиллярах равна примерно , а скорость потока крови в аорте
1. Скорость потока крови в капиллярах равна примерно 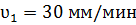 , а скорость потока крови в аорте
, а скорость потока крови в аорте 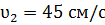 . Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты.
. Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты.
Ответ: 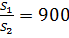 .
.
2. С помощью микроскопа можно измерить скорость течения крови 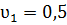 мм/с , а средняя скорость тока крови в аорте
мм/с , а средняя скорость тока крови в аорте 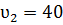 см/с. Учитывая эти данные определить, во сколько раз суммарная площадь поперечных сечений функционирующих капилляров больше площади сечения аорты.
см/с. Учитывая эти данные определить, во сколько раз суммарная площадь поперечных сечений функционирующих капилляров больше площади сечения аорты.
Ответ: 800.
3. На какой максимальной глубине человек может дышать через трубку в воде? Данные взять из задачи 8.
Ответ: h = 1,08 м.
4. В кипятильнике "Титан" уровень воды в баке достигает 85 см. С какой скоростью вытекает вода из крана, расположенного у дна кипятильника?
Ответ: 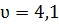 м/с.
м/с.
Вязкость жидкости. Основные понятия и формулы.
1. Градиент скорости dʋ/dx - изменение скорости течения жидкости в направлении, перпендикулярном поверхности слоя (ось Х)
2. Динамическая вязкость η, Па 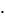 с - коэффициент, который характеризует вязкие свойства жидкости и от которого зависит сила трения между соседними слоями жидкости.
с - коэффициент, который характеризует вязкие свойства жидкости и от которого зависит сила трения между соседними слоями жидкости.
3. Ньютоновская жидкость - жидкость, вязкость которой не зависит от градиента скорости.
4. 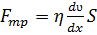 - уравнение Ньютона, где η = const
- уравнение Ньютона, где η = const
5. Неньютоновская жидкость - жидкость, вязкость которой зависит от градиента скорости.
6. Ламинарное течение - течение, при котором слои жидкости текут, не перемешиваясь, скользя друг относительно друга.
7. Зависимость скорости ламинарного течения ньютоновской жидкости от расстояния до оси цилиндрической трубы: 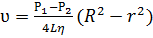 ,
,
где R и L - радиус и длина трубы; r- расстояние от оси трубы; 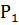
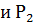 - давления на концах трубы; η- вязкость жидкости.
- давления на концах трубы; η- вязкость жидкости.
8. Турбулентное течение - хаотическое, нестационарное течение жидкости, которое сопровождается образованием завихрений.
9. Число Рейнольдса: Re=ρʋd/η,
где ρ- плотность жидкости, η- Коэффициент динамической вязкости,
ʋ- скорость потока, d- характерный линейный размер трубы или тела, обтекаемого жидкостью.
10. Условие ламинарности течения: Re < 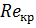 ,
,
где 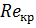 - критическое значение, зависящее от формы сечения трубы или от формы обтекаемого тела. Определяется опытным путем.
- критическое значение, зависящее от формы сечения трубы или от формы обтекаемого тела. Определяется опытным путем.
11. Число Рейнольдса и его критическое значение для ламинарного течения жидкости по цилиндрической трубе: Re=ʋD/η, 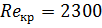 , где D - диаметр трубы.
, где D - диаметр трубы.
12. Формула Пуазейля имеет вид: 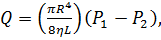
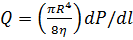 , где Q - объем жидкости, протекающей через горизонтальную трубу за одну секунду, R и L - радиус и длина трубы,
, где Q - объем жидкости, протекающей через горизонтальную трубу за одну секунду, R и L - радиус и длина трубы, 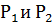 - давления на концах трубы,
- давления на концах трубы,
η - вязкость жидкости.
13. Гидравлическое сопротивление - отношение перепада давлений к объему жидкости, протекающему за 1 секунду: Х = ( 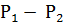 )/Q
)/Q
14. Гидравлическое сопротивление цилиндрической трубы: 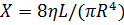 ,
,
Где R и L - радиус и длина трубы, η - вязкость жидкости.
15. Сопротивление последовательного соединения:
Х= 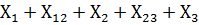
16. Сопротивление параллельного соединения: Х =