А. Помилка середньої арифметичної
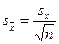 (35)
(35)
де s – середнє квадратичне відхилення; n – об'єм вибірки.
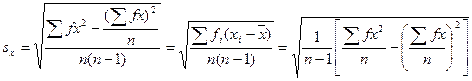 (36)
(36)
Формулами (35) і (36) користуються, коли об'єм генеральної сукупності (N) невідомий або коли вибірка складає її незначну частину (менше 5–10 %) об'єктів генеральної сукупності. У решті випадків її визначають за формулою (37):
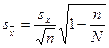 (37)
(37)
Б. Показник точності досліду. Зіставлення середньої арифметичної зі своєю помилкою дає уявлення про точність у визначенні 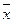 .
.
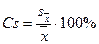 (38)
(38) 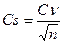 (39)
(39)
Це відношення в дослідній справі носить назву «показника точності досліду». Зазвичай Cs обчислюють не для окремих середніх, а для досліду в цілому, користуючись загальними для досліду середньою арифметичною та її помилкою. Дослід вважають за точний, коли Cs менша за 2 %, і задовільним при Cs не більше 5 %; показник точності досліду, більший 5 %, свідчить про значні помилки у визначенні середньої арифметичної.
2. Розподіл t Ст’юдента.Основні характеристики вибіркового спостереження – середня арифметична і середнє квадратичне відхилення – є, як вказувалося вище, оцінками відповідних параметрів генеральної сукупності – μ і σ. Хоча для більшості сільськогосподарських і біологічних досліджень величина μ невідома, але, користуючись методами статистики, можна визначити межі, в яких вона знаходиться, або, як то кажуть, довірчий інтервал для середньої генеральної сукупності. Відмінність між вибірковою і генеральною середніми може бути якою завгодно величини, проте межі розбіжності між μ і 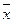 обмежені і визначаються, з одного боку, ступенем варіювання експериментальних даних, а з іншого – рівнем вірогідності, з якою визначається довірчий інтервал. Якщо спостереження варіюють слабко, то інтервал буде вужчий; при значному варіюванні – ширший. Аналогічним чином межі інтервалу зближуються при менш строгому і розширюються при більш строгому підході до обчислення довірчого інтервалу. Залежність між μ і
обмежені і визначаються, з одного боку, ступенем варіювання експериментальних даних, а з іншого – рівнем вірогідності, з якою визначається довірчий інтервал. Якщо спостереження варіюють слабко, то інтервал буде вужчий; при значному варіюванні – ширший. Аналогічним чином межі інтервалу зближуються при менш строгому і розширюються при більш строгому підході до обчислення довірчого інтервалу. Залежність між μ і 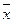 можна виразити рівнянням (40):
можна виразити рівнянням (40):
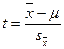 (40)
(40)
Величина t у статистиці носить назву критерій Ст’юдента. Шляхом нескладних перетворень формули (40) можна довести, що 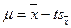 . Оскільки
. Оскільки 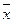 може бути більше або менше μ, то формулу (40) можна перетворити у вираз:
може бути більше або менше μ, то формулу (40) можна перетворити у вираз: 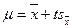 . Звідси довірчий інтервал середньої генеральної сукупності визначається виразом:
. Звідси довірчий інтервал середньої генеральної сукупності визначається виразом: 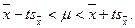 У цій нерівності невідомою величиною є t.
У цій нерівності невідомою величиною є t.
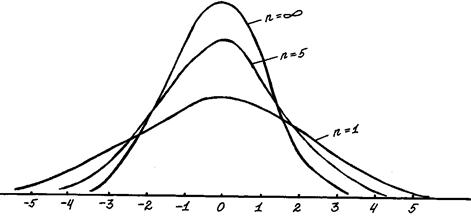
Рис. 7 – Крива розподілів t за різного числа ступенів свободи
Розподіл значень t був досліджений В. Госсетом і увійшло до арсеналу математичної статистики під назвою розподіл Ст’юдента. Було доведено, що цей розподіл симетричний щодо середньої, проте, на відміну від нормального, площа, що знаходиться між віссю абсцис і кривої не постійна і залежить від об'єму вибірки. З рис. 7 видно, що чим менше кількість вибірки (n), тим більше «розтягується» крива. При великому об'ємі вибірки криві розподілу t і нормального співпадають, і практично вся сукупність знаходиться в межах від –3t до +3t. При n=5 на осі абсцис укладається біля ±4,5t, при n=1 – більш ±5,0t.
Значення знаходять за таблицею розподілу Ст’юдента (додаток 4) для різних рівнів істотності. На перетині рядка n (число ступенів свободи) і графи, відповідної вибраному рівню істотності, знаходять число, що показує, на скільки помилок може відхилитися 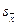 від
від 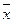 за дії випадкових причин.
за дії випадкових причин.
Приклад. Знайти довірчий інтервал для μ за такими вибірковими даними: 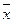 =34 ц;
=34 ц; 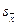 = 1,2 ц; n=10; рівень істотності – 0,05.
= 1,2 ц; n=10; рівень істотності – 0,05.
Спочатку знаходять t (за додатком 4) на перетині рядка 9 (n–1) і стовпця 0,05; t=2,262. Довірчий інтервал визначається як 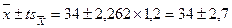 або від 31,3 до 36,7 ц. Ці межі визначають (при вибраному рівні істотності): а) межі можливих випадкових коливань вибіркової середньої і б) довірчий інтервал середньої генеральної сукупності, з якої проведена вибірка. За допомогою критерію t вирішуються багато завдань, що відносяться головним чином до оцінки істотності отриманих у досліді відмінностей, про що йтиме мова в наступних розділах.
або від 31,3 до 36,7 ц. Ці межі визначають (при вибраному рівні істотності): а) межі можливих випадкових коливань вибіркової середньої і б) довірчий інтервал середньої генеральної сукупності, з якої проведена вибірка. За допомогою критерію t вирішуються багато завдань, що відносяться головним чином до оцінки істотності отриманих у досліді відмінностей, про що йтиме мова в наступних розділах.
3. Критерій достовірності різниці.Для дослідника важливо знати чи достовірна отримана, реально існуюча вибіркова різниця, або, за всієї її матеріальній дійсності вона недостовірна. Достовірність вибіркової різниці вимірюється особливим показником, який можна назвати критерієм різниці до її помилки репрезентативності.
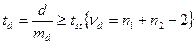 (41)
(41)
де d=|М1–М2| – різниця вибіркових показників;  – помилки вибіркової різниці; m1 і m2 – помилки репрезентативності порівнюваних вибіркових показників; tst – стандартне значення критерію, визначається за таблицею Ст’юдента (додаток 4) для кожного порогу надійності залежно від числа мір свободи; n1, n2 – чисельності порівнюваних вибірок.
– помилки вибіркової різниці; m1 і m2 – помилки репрезентативності порівнюваних вибіркових показників; tst – стандартне значення критерію, визначається за таблицею Ст’юдента (додаток 4) для кожного порогу надійності залежно від числа мір свободи; n1, n2 – чисельності порівнюваних вибірок.
При використанні критерію достовірності можливі два основні випадки. td≥tst – отриманий у досліді критерій достовірності різниці рівний або перевищує стандартне значення критерію, знайдене за Ст’юдентом. В цьому випадку різниця достовірна з певною надійністю, тобто дорівнює за знаком генеральної різниці (між генеральними параметрами). Якщо емпіричний критерій рівний або перевищує стандартне значення нульового порогу, то достовірність встановлена з вірогідністю не менше 0,90. В цьому випадку емпіричний критерій підкреслюється пунктиром. Якщо емпіричний критерій дорівнює або перевищує другий або третій пороги, то надійність складає B2≥0,99 і В3≥0,999, і емпіричний критерій підкреслюється відповідно двома або трьома рисами.
td<tst – отриманий у досліді критерій достовірності різниці менше стандартного значення для мінімального або необхідного порогу вірогідності. У цьому випадку різниця недостовірна, що означає: а) за вибірковою різницею не можна зробити ніякої оцінки генеральної сукупності; б) залишилося невиясненим, яка з двох генеральних середніх більше; в) залишилося недоведеним як наявність, так і відсутність відмінності між генеральними середніми. За мінімальний поріг достовірності в переважній більшості досліджень приймається перший поріг, відповідний вірогідності безпомилкових прогнозів В1=0,95. У деяких випадках за мінімально допустиму вірогідність безпомилкових прогнозів береться вірогідність нульового порогу В0=0,90. Емпіричний критерій при недостовірній різниці підкреслюється хвилястою лінією.
