ЛЕКЦИЯ 4. Уравнения Бернулли и его следствия. Вязкость жидкости. Физические основы гемодинамики

Уравнения Бернулли и его следствия.Линии тока и трубка тока. Условие неразрывности струи.

Течение жидкости изображается линиями тока.

Линия тока- линия, касательные к которым в каждой точке совпадают с направлением вектора скорости частиц. Течение жидкости называется установившимся, стационарным,если скорости частиц в каждой точке потока со временем не изменяются (при этом условии линии тока совпадают с траекториями частиц жидкости).

При стационарном течении линии тока остаются неизменными. Часть потока жидкости, ограниченная линиями тока, образует трубку тока.

Поскольку частицы жидкости не выходят за пределы трубки тока, то через любое ее сечение проходит одно и то же количество жидкости.

Объем Q жидкости, протекающей за единицу времени через любое сечение S, перпендикулярное оси трубки тока, определяется формулой:

Q = S∙υ = const(5.1)

где υ- скорость движения частиц жидкости в данном сечении.

Поскольку, жидкость идеальная и на нее не действию силы трения, то скорости движения частиц во всех точках одного и того же поперечного сечения трубы одинаковы, эта скоростьвходит в уравнение (5.1).

На частицы реальной жидкости действуют силы трения со стороны стенок трубы и со стороны соседних частиц. Поэтому скорость частиц жидкости в поперечном сечении трубы различна: она максимальна в центре трубы и уменьшается до нуля у ее стенок. Входящая в формулу (5.1) будет υ– равная средней скорости течения жидкости в данном сечении.

Уравнение (5.1) выражает условие неразрывности струи. Оно устанавливает соотношение между скоростями течения жидкости в различных сечениях трубки тока:

S₁ /S₂ = υ₂ /υ₁(5.2)

Условие неразрывности струи:при стационарном течении несжимаемой жидкости через любые сечения трубки тока каждую секунду протекают одинаковые объемы жидкости, равные произведению площади сечения на среднюю скорость движения ее частиц.

Если жидкость движется по трубе переменного сечения, то скорость ее движения обратно пропорциональна площади сечения трубок (рис. 7.1).

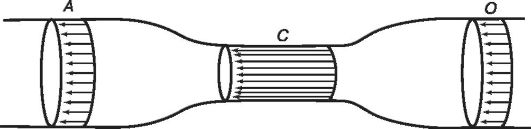
Рис. 5.1.Движение жидкости в трубе с разными сечениями. Длина стрелок изображает среднюю скорость течения жидкости.

Площадь сечения пропорциональна квадратудиаметра трубки (S = πd²/4), поэтому если диаметр трубки в сечении С вдвоеменьше, чем в сечении А, то площадь поперечного сечения С в четыре раза меньше, чем площадь сечения А. Следовательно, и скорость потока в сечении С будет в четырераза больше, чем в сечении А.

Уравнение неразрывности струи при протекании крови в сосудах

Кровеносная система человека - это сложная замкнутая система эластичных трубок разного диаметра. В нее входят: аорта, артерии, артериолы, капилляры, венулы, вены. Из сердца кровь поступает в аорту, а оттуда распределяется по главным артериям, затем по более мелким и в конце концов расходится по миллионам мелких капилляров. По венам кровь возвращается в сердце. (Один цикл движения крови длится в среднем 20 с. За сутки сердце перегоняет по всем сосудам до 10 000 л крови!) Скорость кровотока в разных сосудах различна. Ориентировочные значения этой скорости представлены в табл. 5.1.

Таблица 5.1.Скорость и давление крови в различных сосудах

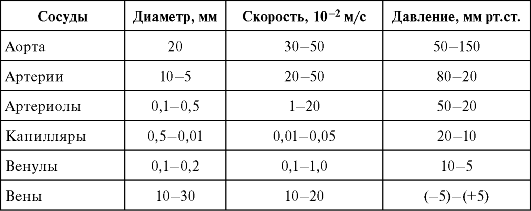
На первый взгляд, кажется, что приведенные значения противоречат уравнению неразрывности - в тонких капиллярах скорость кровотока примерно в 1000 меньше, чем в артериях. Однако это несоответствие кажущееся. Дело в том, что в табл. 5.1 приведен диаметр одного сосуда. Эта величина действительно уменьшается по мере разветвления. Однако суммарная площадь разветвления возрастает. Так, суммарная площадь всех капилляров (около 2000 см²) в сотни раз превышает площадь аорты - этим и объясняется такая малая скорость крови в капиллярах. Малая скорость кровотока в капиллярах необходима для обеспечения эффективного обмена между кровью и тканями.

Уравнение Бернулли

Рассмотрим течение идеальной жидкости через тонкую трубку тока разного сечения расположенную под углом.

Выделим в ней два участка разного сечения S₁ и S₂. Вследствие неразрывности жидкости течение идеальной жидкости в этих сечениях будет с разными скоростями ʋ₁ и ʋ₂ .

Объем жидкости, протекающей за единицу времени через любое сечение, перпендикулярное оси трубки тока: Q = S₁ʋ₁ = S₂ʋ₂ = Sʋ = const,

где S- площадь сечения; ʋ- скорость течения.

Обозначим давления жидкости в этих сечениях Р₁ и Р₂.

Используя закон сохранения энергии можно доказать, что в этих сечениях выполняется следующее соотношение:

Р₁ + ρʋ₁²/2+ ρgh₁ = Р₂ + ρʋ₂²/ 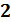+ ρgh₂-

При стационарномтечении идеальной жидкости полное давление, равна сумме статического , динамического и гидростатического давлений, одинаково во всех поперечных сеченияхтрубки тока.

Равенство Р + ρ 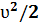+ ρgh = const. -называетсяуравнением Бернулли,

гдеР - статическое давление, которое оказывают друг на друга соседние слои жидкости (его можно измерить манометром, который движется вместе с жидкостью), ρgh - давление, создаваемое весом вертикального столба жидкости высотой h, ρ 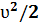- динамическое давление, обусловленное напором движущейся жидкости.