Построение эпидемической кривой.
В реальных экосистемах существует множество трофических уровней и внешний вид организации таких уровней довольно сложен. Однако нам надо еще указать на одно мощное лимитирование, которое широко распространено в природе. Речь идет о болезнях, которые могут резко ограничить численность Х в модели (1) и ниспровергнуть теорию Мальтуса. Действительно, известно, что эпидемия чумы в 15-м веке в Европе, например, унесла 25% жизней всего населения Европы (т.е. умерло около 25 млн. человек, больше, чем в 1-й мировой войне). Это пример распространения инфекционных заболеваний, динамику которых в (1) можно представить так:
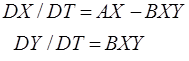 (11)
(11)
Здесь производится учет появления численности заболевших ("заразных") особей, которые путем контакта со здоровыми особями (слагаемое -BXY) заражают последних, уменьшая их численность. Скорость процесса заражения DY/DT и соответственно прироста численности заболевших Y пропорциональна числу контактов X и Y. Причем, коэффициент B- учитывает интенсивность контактов между здоровыми особями X и больными особями Y, т.е. со скоростью BXY здоровые X переходят в класс больных Y (скорость прироста последних растет пропорционально контактам X и Y). В реальной ситуации заболевание распространяется быстро и слагаемым AX пренебрегаем, т.е. имеем следующее рекуррентное соотношение, которое используется в компьютерном моделировании динамики распространения заболеваний:
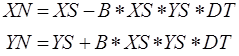 (12)
(12)
В действительности интерес представляет не динамика изменения X и Y, а динамика DY/DT= B*XN*YN. Такая зависимость графически представляется эпидемической кривой- колоколообразной линией с максимумом. Именно эпидемическая кривая несет максимум прогноза для органов здравоохранения и ветнадзора, т.к. возможности борьбы с заболеванием ограничены (органы здравоохранения и ветнадзора за неделю, например, могут оказать помощь ограниченному количеству индивидуумов или особей). Внешний вид эпидемической кривой представлен на рис.3.
Ее расчет на ЭВМ представлен программой в приложении 3. Следует отметить, что в реальной ситуации заболевших изолируют, или они приобретают после болезни иммунитет и исключаются из процесса контакта с Y. В этом случае появляется численность изолированных Z, которые могут вымирать со скоростью GZ. Тогда общая модель примет вид:
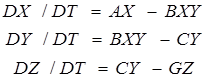 (13)
(13)
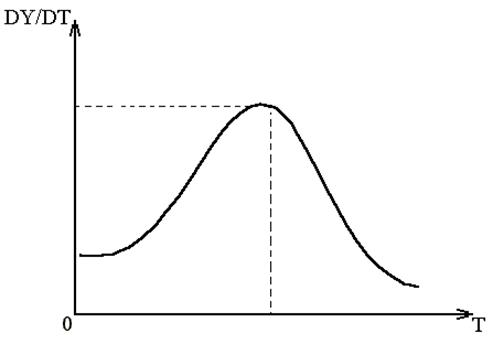
Рис.3. Эпидемическая кривая
и она наиболее полно представляет динамику развития инфекционного процесса в популяции.
При проведении противоэпидемических мероприятий можно иммунизировать восприимчивых X со скоростью D и в правой части первого уравнения из (13) появится слагаемое "-D". В этой связи возникают задачи оптимального проведения противоэпидемических мероприятий с минимумом экологических потерь для общества. Однако, это отдельная большая проблема. Таким образом, используя модели (11), (12), (13) и Приложение 4, Вы можете смоделировать динамику эпидемии гриппа или другого инфекционного заболевания в растущей популяции или других заболеваний в различных других сообществах животных или растений. Такие прогнозы важны для принятия срочных мер по борьбе с этими заболеваниями в природе и обществе. Вместе с тем понятно, что непринятие эффективных мер чревато резким снижением общей численности X любой популяции. Следует отметить, что в этом вопросе должны быть некоторые разумные ограничения. Сказочная мечта человечества о победе над всеми болезнями- блеф, идиллия, т.к. болезни выполняют и эволюционные функции, функции естественного отбора. Сейчас можно уже утверждать, что накапливается груз генетических ошибок в популяции человека. Последствия этого явления могут быть катастрофическими.
Один из самых страшных и прогнозируемых сегодня эффектов- преодоление целым рядом патогенных микроорганизмов межвидового барьера. Свидетельство тому- вирус СПИДа (болезнь обезьян), коровье бешенство (болезнь БКЯ), гонконгский куриный грипп и т.д.
Опасность здесь заключается в быстроте развития инфекции и, практически, отсутствии противоэпидемических мероприятий (кроме снижения коэффициента B в (11) - изоляции здоровых от больных). Такое развитие процесса можно рассматривать как обычную отрицательную связь (лимитирующий фактор). Однако это лавинообразный процесс и останутся в живых только те особи, которые имеют малую восприимчивость или легко (с низким летальным исходом) переносят заболевания. В целом такой процесс можно рассматривать как некоторую генетическую чистку популяции человека или животных. В любом случае можно твердо утверждать, что теория Мальтуса об экспоненциальном росте числа жителей Земли неверна, а использование математических (биофизических) методов в экологии и медицине значительно облегчает задачи прогноза динамики развития заболеваний в экосистемах, т.е. делает теорию эпидемий и экологию строгими формализованными науками.
Приложение 3
Простейшая модель распространения инфекционных заболеваний в растущей популяции имеет вид (11), которая при очень малых A и с учетом разностных определений DX и DY принимает вид (12):
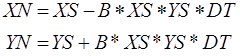 (12)
(12)
Поскольку, как указывалось выше, DY=YN-YS=B*XS*YS *DT, то мы будем считать сначала XN и YN а затем DY, но в модернизированном виде, т.е.
DY=M*B*XN*YN*DT.
Здесь М- некоторый масштабный множитель, который Вам придется подбирать экспериментально , т.е. изменения DY весьма малы в сравнение с Х и Y. С учетом сказанных замечаний программа, реализующая систему (12), примет следующий вид:
10 CLS : SCREEN 9, 1, 0
20 INPUT "B=", B: INPUT "X0=", X0: INPUT "L=", L:
25 INPUT "Y0=", Y0: INPUT "DT=", DT: INPUT "K=", K: INPUT "M=", M
30 XS = X0 - B * X0 * Y0 * DT - L * X0: YS = Y0 + B * X0 * Y0 * DT:
35 DM = YS
40 FOR I = 2 TO K
50 XN = XS - B * XS * YS * DT - L * XS: YN = YS + B * XS * *YS * DT:
DY = M * B * XN * YN * DT + 10: T = 30 * I * DT + 70
60 DYN = 200 - DY: PSET (T, DYN), 14
61 IF DY > DM THEN DY = DM: boln! = DM: vrem! = T ELSE
70 XS = XN: YS = YN: NEXT I
80 LINE (60, 200)-(60, 20), 12: LINE (60, 200)-(600, 200), 12
90 LOCATE 16, 54: PRINT " DY = DY(T) "
91 LOCATE 20, 14: PRINT "Максимальное значение и время"; boln!; vrem!
Задание 3.
Наберите эту программу на ЭВМ. Задайте некоторые гипотетические начальные условия модели (12): B=0.01, X0=150, Y0=0.01, M=50
Зарисуйте график эпидемической кривой с экрана монитора. Изменяя масштаб М в программе добейтесь, что бы кривая занимала половину экрана. Зачем надо вводить масштаб М? Из графика определите в какой момент времени Tmax имеем максимум эпидемической кривой? Внимание! Вся линия Т имеет 600 единиц! Почему 600?
Что будет, если в (11) A¹0? Как изменится эпидемическая кривая при прочих равных условиях, если в программе ввести A=0.05? Измените программу с учетом A и ответьте на поставленный вопрос. Произведите учет миграции МХ в правой части уравнений (11) и (12). Как миграция МХ влияет на эпидемическую кривую? Существенно, что миграция МХ может рассматриваться и как специфическая (например, иммунизация) или неспецифическая (профилактика перед началом эпидемии или эпизоотии). При этом, используя такие мероприятия, можно управлять динамикой эпидемического процесса.
Проанализируйте последнее утверждение и докажите это экспериментально с использованием ЭВМ и видоизмененной программы с учетом МХ. Выводы проиллюстрируйте полученными эпидемическими кривыми.
Лабораторная работа № 1.4
