Моделирование эпизоотий в экосистемах.

УСТОЙЧИВОСТЬ СИСТЕМ "ХИЩНИК- ЖЕРТВА",

"ПАРАЗИТ- ХОЗЯИН"

Цель работы:

1.Обучающийся должен знать:

понятия популяционного взрыва, виды лимитирования в популяциях, внутривидовую и межвидовую конкуренцию, вопросы динамики распространения эпизоотий. Знать причины возникновения этих процессов и примеры из живой природы.

2. Обучающийся должен уметь:

составить и объяснить математическую модель указанных процессов, набрать программу на ЭВМ и смоделировать любой из этих процессов на ЭВМ. Сделать вывод о влиянии параметров модели на динамику процессов на основании компьютерного моделирования. Вычислять точку покоя двухвидовой модели и давать её классификацию по типу устойчивости.

Оборудование:ЭВМ с принтером, карандаши, бумага.

Практическое значение работы:

Многие процессы в биологическом мире имеют колебательный характер: работа сердца, дыхание, фотолиз, генерация потенциалов на мембранах клеток и т.д. Эти процессы требуют количественного и качественного описания. В основе теории этих процессов часто лежат простейшие 2-х видовые (двухпуловые) нелинейные модели Лотка- Вольтерра. Исследование этих моделей, стационарных режимов их функционирования, динамики этих процессов на фазовой плоскости- основные задачи этой работы.

Бюджет времени:выполнение практической работы – 2 часа, время для самоподготовки – 4 часа, лекции – 2 часа.

ЛИТЕРАТУРА

1. Динамическая теория популяций./ А.А. Гимельфарб, Л.Б. Гинзбург, Р.А. Полуэктов и др.; под редакцией Р.А. Полуэктова.- М.: Наука, 1974.- 456 с.

2. Варфоломеев С.Д., Гуревич К.Г. Биокинетика: Практический курс.- М.: ФАИР- ПРЕСС, 1999.- 720 с.: ил.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ

"Самоподготовка"

Цель этапа: 1. Повторить исходную информацию, необходимую для понимания изучаемой темы.

2. Проверить качество усвоения новой информации перед выполнением работы.

I. Исходный уровень знаний.

Для изучения темы необходимо повторить основные понятия экологии, методы компьютерного моделирования экосистем, понятие фазовой плоскости и особых точек моделируемой системы

II. Изучив блок информации и учебную литературу, обучаемый должен ответить на следующие вопросы и решить задачи.

1. Что такое экспоненциальный рост раковых клеток? Чем он обусловлен? Что такое экспоненциальная зависимость?

2. Что такое системы "хищник- жертва", "паразит- хозяин". Поясните примерами.

3. Как в 2-хвидовых системах реализуется принцип обратных связей в биосистемах? Поясните примером.

4. Расскажите программу модели экспоненциального роста раковых клеток.

5. От чего зависит частота колебаний численности х и у в модели "паразит- хозяин"? Как можно изменить амплитуду колебаний х и у в модели на ЭВМ? Как находится стационарная точка в этих моделях?

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО II ЭТАПУ:

“Выполнение лабораторной работы”

Цель этапа: Исследовать методами математического моделирования динамику систем "хищник- жертва" и "хозяин- паразит" в зависимости от введенных кинетических констант. Для достижения цели необходимо экспериментально проверить (и доказать!), что частота колебаний w зависит от значений параметров А1 и А2 примерно по формуле . Проверить, как зависит от А1 иА2, В1 иВ2 амплитуды колебаний и координаты точки покоя. Рассчитать эти координаты теоретически и сравнить с экспериментом.

Методические указания по III этапу:

“Получение зачета по лабораторной работе”

Перед выполнением работы обучаемый должен изучить все методические указания, ответить на вопросы и решить задачи из раздела “Самоподготовка”.

После выполнения II этапа необходимо оформить протокол работы и подписать у преподавателя, а затем приступить к оформлению работы в тетради.

Работа считается зачтенной после сдачи преподавателю отчета по теоретическому и практическому разделам работы.

Блок информации

Исследование природных экосистем- длительная и трудоемкая работа. Ее сложность еще заключается и в том, что ставить эксперименты на экосистемах опасная задача с возможностью очень тяжелых последствий для природы. Один из таких экспериментов ставит сейчас все человечество и результаты пока весьма плачевны. Вместе с тем имеется возможность реализовать желания любого исследователя- эколога не затрагивая природу. Это реализуется с помощью ЭВМ и математических моделей. В этой связи компьютерное моделирование-это весьма перспективное и безопасное направление в экспериментальной экологии и биофизике.

В рамках такого подхода уже решены многие задачи оптимального сбора урожая (отстрела животных и т. д.) в эксплуатируемых экосистемах; задачи устойчивости экосистем к неблагоприятным антропогенным воздействиям, устойчивости экологических сообществ к эпизоотиям и многие другие задачи устойчивости прикладного характера. В целом, математическая экология и теория эпидемий- весьма перспективное направление теоретической и экспериментальной биофизики популяций, а знакомство с ее методами и возможностями- необходимый элемент познания биофизики и экологии в целом.

Вместе с тем математическая экология (МЭ)- это отдельная наука со своим аппаратом, методами и обеспечением, которая использует все биологические понятия из экологии, но дает им свою специфическую трактовку. Фактически МЭ- это популяционная биофизика (ПБ) по методам исследования.

Наука начинается там, где есть математика- этот афоризм весьма уместен здесь, при изучении ПБ или математической экологии. Рассмотрение этой науки начнем с ряда задач.

1. Модель популяционного взрыва.

В природе известны эффекты резкого возрастания численности отдельных популяций, приводящие к глобальным изменениям не только экосистем, но и эколандшафтов с геологическими изменениями. Это примеры популяционных взрывов численностей леммингов на севере Скандинавии, саранчи в Африке, кроликов в Австралии и, наконец, фантастическая ситуация с “вечным хлебом” у писателя Беляева в его известном произведении. Как протекают эти процессы и каковы их закономерности? Попробуем ответить на эти вопросы с помощью математических моделей.

Пусть численность некоторого вида описывается функцией времени C=C(Т). Тогда, если предположить, что скорость DX/DT прироста численности особей X= X(T) будет зависеть от численности особей X(T) в данный момент времени, т.е.

DX/DT=AХ, (1)

где A - коэффициент скорости прироста численности особей X(T), то динамика процесса опишется функцией:

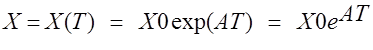, (2)

где X0- начальная численность популяции в момент времени T=T(0). Это означает экспоненциальный рост численности X со временем, т.е. X является показательной функцией от T. Посмотреть график этой зависимости на экране монитора ЭВМ Вы сможете очень просто, если воспользуетесь методом Эйлера, т.е. надо взять в качестве прироста численности DX=XN-XS (разность между наращенным (новым) значением- XN и старым значением- XS). Тогда получим рекуррентное соотношение, по которому мы вычислим последующее значение численности популяции (XN) через предыдущее значение (XS). Отметим, что это приращение DX происходит за время DT. Таким образом, если "заставить" ЭВМ выполнить в цикле последовательные итерации (расчет новых значений через старые XS) и наносить получаемые точки на экран монитора, то мы увидим зависимость X(T) в виде графика (экспоненциальной кривой), на который и указывал Мальтус в своей работе. В приложении 1 дается подробное описание программы расчета X(T) на ЭВМ в Basic, которую Вам необходимо набрать и исследовать эту зависимость для разных начальных условий (к ним относится начальная численность X и константа скорости прироста популяции A). Внешний вид этой зависимости приведен на рис.1. Из рисунка видно, что, имея меньшую начальную численность (X0₂), но большую скорость роста (A₂ ), можно быстро догнать (и перегнать) в численности другую популяцию (X0₁). В любом случае численность нарастает неограниченно и быстро.

Процессы такого вида имеют место и при росте числа раковых клеток, когда их численность в организме ничем не ограничивается и динамика процесса будет определяться только величиной коэффициента А. Облучение опухоли может резко изменить А и даже сделать А®0, что ограничит процесс развития опухоли. При этом хирургические операции могут только снизить X(T), что представляется моделью:

DX/DT = AX – M (3)

Очевидно, что при оперировании опухоли важно сделать X0=0, т.е. удалить все раковые клетки.

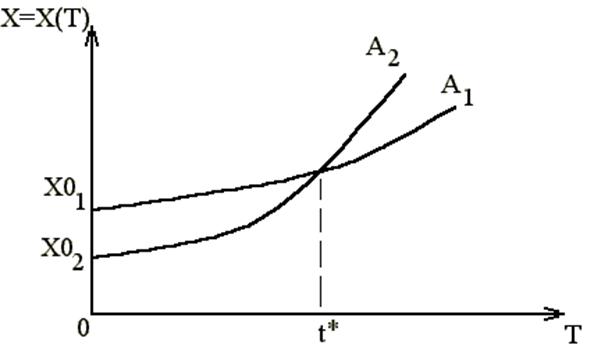
Рис. 1.Модель популяционного взрыва

Приложение 1.

В соответствии с формулой DX/DT=AX имеем, что приращение численности DX за интервал времени DT равно

DX=XN-XS=A*XS*DT (4)

Отсюда новое значение численности ХN определяется через предыдущее значение XS по формуле

XN=XS+A*XS*DT, (5)

где знак ²* ² означает умножение.

Всю программу расчета мы представим с описанием в Qbasik, при этом мы специально будем нумеровать строчки (хотя это делать и не обязательно).Итак вначале используем оператор очистки линий экрана CLS (clean line screen) и выберем тип экрана, что связано с размерами букв и числом точек, умещающихся по горизонтали (например, 640 точек) и по вертикали (360- 380, в зависимости от типа монитора). Тогда первая строка (назовем ее числом 10) имеет вид:

10 CLS: SCREEN 9, 1, 0

Здесь знак ² : ² означает разделение двух разных операций (вместо двоеточия можно поставить новую строку). Цифра 9- означает функциональный тип экрана, а 1 и 0 означает, что на черном фоне будут белые линии (буквы).

В следующей (20- ой) строке сделаем ввод в ЭВМ начальных данных условий для расчета моделей популяционного взрыва. Начальные условия вводятся оператором INPUT (ввод) и к ним относятся: коэффициент скорости прироста численности А; начальная численность популяции Х0; интервал дискретизации времени DT(чем он меньше тем точнее расчет) и общее число шагов счета K, которое связано с реальным текущим временем T по формуле

T=I*DT, Т конечное = K* DТ.

Итак вводим начальные данные:

20 INPUT²A=²,A: INPUT²X0=²,X0: INPUT ²DT=², DT: INPUT ²K=²,K

Внимание! Очень внимательно относитесь к знакам препинания! Далее рассчитаем значение XS из (4), считая, что XN=XS, а XS=X0, т. е.

30 XS=X0+A*X0*DT,

т. е. мы сделали первую итерацию.

Для дальнейшего счета нужно организовать цикл с переменными индексами, например:

40 FOR I=2 TO K

50 XN=XS+A*XS*DT: T=DT*I+100

При этом вычисляемые значения XN надо наносить на график в виде точек, где ось аргументов представляет Т, а ось ординат- XN. Для этого мы введем, отступив на 100 точек вправо, реальное время Т (его можно масштабировать), а построение по вертикали- задача немного сложней. Дело в том, что отсчет на экране монитора производится не снизу вверх, а наоборот. Поэтому нам надо опуститься вниз (например на 200 точек) и потом от этого значения вычитать XN, что реально будет соответствовать привычному подъему графика функции X=X(T).

Тогда имеем реальное некоторое U, представляющее искомое X:

60 Y= 200-XN : PSET (T,Y), 14

Здесь оператор PSET устанавливает на экране некоторую точку цветом 14 (желтый цвет) с координатами Т и U. Множество таких точек образуют сплошную линию- график функции C=C(T).

Для расчета в цикле нам надо каждый раз очищать старую ячейку памяти XS и туда заносить новые значения XN, полученные в каждой итерации, т. е.

70 XS=XN

После этого мы требуем смены индекса I (оператор NEXT) и процедура повторяется много раз, до тех пор пока станет I=K, тогда счет остановится сам или надо записать оператор STOP, т. е.

80 NEXT I

¼¼¼¼¼¼¼¼

120 STOP

Для того, что бы график имел классический вид надо начертить оси координат C и T и подписать их. Делается это оператором LINE и LOCATE, т. е.:

100 LINE (100, 200)- (100,10), 12 :LINE (100,200)-(500, 200),12

110 LOCATE 3,4 : PRINT ²X=X(T)² :

LOCATE 23, 62 : PRINT ²реальное время T²

Итак Вы должны набрать все 120 строк последовательно, записать их в память ЭВМ и запустить программу нажатием клавиши F5 (run). Давайте будем брать значения Х0=4 (особям); DT=0.01; A=0.1 или 0.01 (сравните графики для этих 2-х разных А!) и K=50000. Обратите внимание, что уменьшая DT мы должны увеличивать K! Иначе график получится очень короткий на экране монитора.

Таким образом Вы можете моделировать процесс экспоненциального роста численности популяции Х во времени и посмотреть, как меняется эта численность в зависимости от условий существования вида Х.

Задание 1.

1. Наберите программу расчета Х=Х(T) на ЭВМ;

2. Введите указанные значения А, DT, K, X0 последовательно и зарисуйте с экрана монитора полученные графики;

3. Сделайте анализ и вывод о зависимости кривой от значений Х0 (Х0=4 и Х0=2) и коэффициента А;

4. Какая из популяций будет иметь большую численность в момент времени Т=100, если у первой Х0= 4 и А= 0,05,а у второй Х0= 2, но А= 0,08? (Ответ проиллюстрируйте на ЭВМ.)