Сердечно- сосудистой системы (ссс) человека.
Цель работы:
1. Обучающийся должен знать: биологическую и математическую трактовку понятия покоя биологических динамических систем (БДС), основные методы идентификации стационарных режимов динамических систем (метод наименьших квадратов, метод минимальной реализации - ММР), основные методы определения параметров ССС (частота пульса, САД и ДАД, скорость пульсовой волны).
2. Обучающийся должен уметь: измерять параметры ССС с помощью лабораторной установки, строить модели системы регуляции пульса с помощью ЭВМ и программы.
Практическое значение работы:
Стационарные режимы БДС (удержание параметров биологической системы в фиксированных значениях)- весьма важный режим их функционирования. Особое значение при этом имеет проблема идентификации БДС в режиме "черного ящика", когда внешние (наблюдаемые) параметры БДС как бы не меняются, но внутри система может испытывать существенные структурные перестройки, которые в ряде случаев могут закончиться гибелью БДС (вспомним синдром внезапной смерти при дезритмии в ССС). В этой связи использование методов идентификации БДС позволяет предсказывать изменение порядка модельной системы, возникновение бифуркаций или даже хаоса в ней. Одному из методов (ММР) идентификации моделей БДС и посвящена данная работа
Бюджет времени: на изучение теории (самоподготовка)- 4 часа, выполнение работы- 2 часа, лекции- 2 часа.
Литература
1. Анохин П.К.
2. Амосов Н.М., Бендет Я.А. Физическая активность и сердце.- Киев, 1989г.,214 с.
3. Еськов В.М., Филатова О.Е. Компьютерная идентификация респираторных нейронных сетей. Пущино., 1994. 94 с.
4. Косицкий Г.И. Цивилизация и сердце. Москва 1977 г., 183 с.
5. Скупченко В.В., Милюдин Е.С. Фазотонный гомеостаз и врачевание.- Самара, 1994 г. 256с.
6. Судаков К.В., Надирашвили С.А., Швыркова Н.А. и др. Теория системогенеза, Москва 1997 г., 566 с.
7. Сливинских В., Шимоните В. Минимальная реализация и формантный анализ динамических систем и сигналов. Вильнюс: Мошлас,1990. 230 с.
8. Чазов Е.И. Руководство по кардиологии. Москва 1982, 4 т.
9. Kalman R.E. On minimal partial realization of linear input/output map in aspects of network and system theory//Kalman R.E. and Claris N.D., Holt, Rinehart and Winstont. New York, 1971.
10. Lindquist A., Gragg W.B. On the partial realization problem.// Linear Algebra Appl. 1983. 50. p.277- 319.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ
“Самоподготовка”
I. Перед изучением работы необходимо повторить понятия модели и математической модели (ММ), понятия вектора состояния, дифференциальные и разностные уравнения, метод наименьших квадратов, основные элементы регуляции ССС (симпатическая и парасимпатическая регуляция сердца, роль гормонов), понятия работы и мощности, выполняемой человеком в результате физических упражнений.
II. Для самоконтроля новых знаний необходимо ответить на следующие вопросы:
1. Как измеряется систолическое и диастолическое давления, какова их природа?
2. Что такое быстрая и медленные компоненты в регуляции частоты сердечных сокращений (ЧСС) ?
3. За счет чего изменяется АД и ЧСС в результате короткой физической нагрузки?
4. В чем сущность метода "черного ящика"- основы метода минимальной реализации (ММР)?
5. Как правильно выполнить измерения и идентификацию БДС в данной исследовательской работе?
6. Охарактеризуйте основные типы реакции ССС в ответ на дозированные нагрузки.
7. Что такое дистонический и ступенчатый тип реакции? Можно ли их идентифицировать с помощью ММР?
8. Как характеризуют собственные значения матрицы линейного приближения изучаемую БДС?
9. Что такое Перронов корень и как он характеризует БДС?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО II ЭТАПУ:
“Выполнение лабораторной работы”
1. Перед началом опытов у испытуемого измеряют ЧСС, САД, ДАД.
2. Испытуемый выполняет 30 приседаний (если абсолютно здоров) за 30 сек или (если имеется легкое недомогание, девушки) за 1 мин по метроному. Затем каждые 30 сек (или 1 мин) измеряют ЧСС, САД, ДАД и заносят их в таблицу. Желательно измерения провести не меньше 16 раз (8 раз во втором случае) за восстановительный период. Существенно, что бы нагрузка не ощущалась как предельная, в противном случае испытания следует прекратить. Желательно испытания проводить на спортсменах.
3. Полученную таблицу данных сравнивают с исходными (до нагрузки – испытаний) данными и разницу между полученными и исходными результатами заносят как марковские параметры (поочередно для ЧСС, ДАД, САД) в ЭВМ (во 2-м разделе mra.exe). С помощью ЭВМ вычисляют матрицу А, С и собственные значения матрицы А. Результаты вносят в таблицу 2 (таблица 1- результаты измерений). Делают выводы о значениях собственных значений А и о наличии Перронова корня (или отсутствии!)
Таблица 1
| ЧСС | dx | САД | dy | ДАД | dz | |
| Исходн. | ||||||
| 1 мин | ||||||
| 2 мин | ||||||
| ¼ | ||||||
| 8 мин |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО III ЭТАПУ:
“Получение зачета по лабораторной работе”
Перед выполнением работы обучающийся должен изучить все методические указания, ответить на вопросы и решить задачи из раздела “Самоподготовка”.
После выполнения II этапа необходимо оформить протокол работы и подписать у преподавателя, а затем приступить к оформлению работы в тетради.
Работа считается зачтенной после сдачи преподавателю отчета по теоретическому и практическому разделам работы.
Блок информации
Стационарные режимы функциональных систем организма.
Организм человека – это совокупность многих функциональных систем. Эти системы испытывают постоянные возмущения со стороны внешней и внутренней среды. Центральная нервная система (ЦНС) обеспечивает некоторую стабильность работы всех этих функциональных систем. Например, работа сердца, частота дыхания в норме приблизительно находятся около некоторого стационарного состояния. Математически это выглядит так, что скорости изменения параметров x этих систем (dx/dt) приблизительно равны нулю (т. е. dx/dt=0 или x=const).
Однако внешние возмущения приводят к dx/dt¹0. Возникает вопрос: как оценить момент, когда мы переходим от x=const к x=x(t), т.е. x¹const? Ответ на этот вопрос представлен в данной работе.
1. Понятие динамических систем в живой и неживой природе.
Любая техническая или биологическая система может быть описана некоторыми переменными величинами, которые можно трактовать как координаты некоторого вектора состояния х данной БДС, т.е.
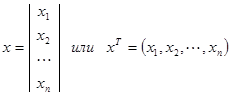 ,
,
где х – вектор-столбец, хт – вектор-строка, xi = xi(t).
Координаты xi(i=1,2, ... ,n) такого вектора могут иметь различный смысл. Например, для движущегося механизма xi- это его координаты в пространстве (X,Y,Z) и во времени t, а так же величины изменения переменных (x,y,z) во времени, т.е. скорости dx/dt = Vx, dy/dt= Vy, dz/dt= Vz. Зная эти семь переменных мы можем характеризовать полностью движение любого тела в пространстве.
Отметим, что в этом примере x1=x, x2=y, x3=z, x4=Vx, x5=Vy, x6=Vz являются функциями (переменными) от аргумента t, т.е. вектор x=(x1,x2,...,x6) состоит из 6-ти компонент. Его можно представить в виде вектора в 6-ти мерном пространстве, но графически это сделать трудно. Тем не менее мы будем говорить в дальнейшем о задании любого вектора x состояния БДС в n-мерном пространстве, которое будем называть фазовым пространством. Например, если мы имеем дело с функциональной системой (ФС) организма (по П. К. Анохину ФС – это комплекс взаимодействующих компонентов для получения полезного для организма результата), то она описывается своими переменными величинами. Одной из основных ФС человека является кардио-респираторная система (КРС), которая обеспечивает адаптивную реакцию организма на увеличение физической нагрузки или при эмоциональных стрессах. В этих случаях компонентами вектора состояния x ФС будут величины частоты сердечных сокращений (ЧСС), систолическое (САД) и диастолическое (ДАД) артериальное давление (АД), показатели электрокардиографии (ЭКГ), частоты и глубины дыхания и т.д. Все эти компоненты xi характеризуют КРС как в покое, так и при нагрузках. Понятно, что в покое xi»const, т.е. dx/dt»0 [3].
2. Стационарные режимы биологических динамических систем (БДС).
Их классификация.
Описание динамики поведения ФС может быть представлено в виде системы дифференциальных или разностных уравнений (ДУ и РУ), например, в виде
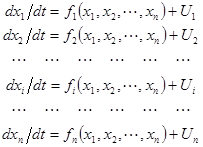 , (1)
, (1)
где fi(x1, x2, ..., xn)- некоторые функции, а Ui– учитывает внешние воздействия на ФС.
Отметим, что (1) можно записать в векторной форме dx/dt=Ax+U, где A является некоторой матрицей, элементы aij, которой представляют величины воздействия j-й компоненты вектора x на i-й компоненту. Например, модель вида
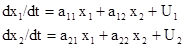 (2)
(2)
имеет матрицу 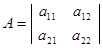 , вектор xТ=(x1,x2), вектор UТ=(U1, U2). Она может описывать реципрокные взаимодействия в ЦНС или мышечной системе (между мышцами- агонистами, т.е. флексорами-экстензорами). Модель (2) использовалась Н.Рашевским для моделирования поведения водителя за рулем автомобиля. Важно отметить, что в стационарном состоянии (dx/dt=0) система (1) переходит в систему обыкновенных (алгебраических) уравнений, из которой можно определить координаты (x0i) точки покоя (ТП) x0.
, вектор xТ=(x1,x2), вектор UТ=(U1, U2). Она может описывать реципрокные взаимодействия в ЦНС или мышечной системе (между мышцами- агонистами, т.е. флексорами-экстензорами). Модель (2) использовалась Н.Рашевским для моделирования поведения водителя за рулем автомобиля. Важно отметить, что в стационарном состоянии (dx/dt=0) система (1) переходит в систему обыкновенных (алгебраических) уравнений, из которой можно определить координаты (x0i) точки покоя (ТП) x0.
Очевидно, что в биологии может быть x0=0 (полный покой, если внешние возмущения Ui=0) или x0>0. Например, если человек не испытывает нагрузки, то ЧСС (n) и АД (P) могут быть (x1=n, x2=P) постоянными, т.е. x01=C1, x02=C2.
Итак, возможны нулевые и ненулевые значения x0. Для модели (2) x0>0 всегда, если U>0 (докажите!). Это значит, что для открытых (с внешним драйвом) систем их стационарные состояния ненулевые. Полное описание точек покоя модели (2) и их представление на фазовой плоскости (возможны ТП типа узла, фокуса, седла и др.) представлено в приложении 1 и демонстрируется в специальном файле TPF.exe. Важно отметить, что эти ТП могут быть устойчивыми и неустойчивыми. В первом случае внешние возмущения в БДС выводят её из состояния равновесия, в которое БДС возвращается спустя некоторое время (например, устойчивый фокус). Во втором случае траектория на фазовой плоскости с течением времени уходит в бесконечность- система неустойчива.
3. Методы идентификации БДС в стационарных режимах (СР).
Итак, в стационарных режимах БДС имеет значение вектора состояний x0=const, что очень легко идентифицировать по наблюдениям компонент x, т.е. величин xi. Однако сама БДС может находиться в разных (внутренних) состояниях, которые можно исследовать путем предъявления на вход БДС некоторых внешних (возмущающих) стимулов (например, Ui=Ui(t)). Мы будем использовать подход "черный ящик", когда по анализу входных (Ui) и выходных (y) величин для неизвестной БДС можно построить некоторую адекватную математическую модель вида (1) или (3):
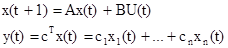 (3)
(3)
Модель (3)- это модель в виде разностных уравнений, где U(t)- величина входных воздействий, B- вектор оценки U(t), cТ- вектор- строка вклада (влияния) переменных xi(t) на величину выхода БДС- y(t), а x(t+1) и x(t)- последующие и предыдущие значения вектора x, взятые через шаг (и интервал времени) равный 1.
В настоящей работе используется метод минимальной реализации (ММР), когда находятся модели (1) или (3) с минимальным порядком (размером вектора х) n и минимальной погрешностью P (в процентах, практически, мы требуем P < 5%). Последнее означает, что отклонение теоретических значений yi (вычисленных из (1) или (3)) не должно превышать 5% от полученных на практике у (фактически, набор выходных величин yi), которые называются марковскими параметрами. Используется разработанная программа, реализующая ММР для данной БДС, которая находится в линейном (или квазилинейном) состоянии. Проверить такое состояние легко. Для этого надо кратно увеличить входной стимул U и убедиться, что так же кратно увеличился сигнал y(t). Во многих случаях линейность БДС можно просто постулировать. Например, мы можем считать, что ССС в покое является линейной системой. Тогда даем нагрузку испытуемому (например, 30 приседаний за 30 сек!) и наблюдаем ответную реакцию (изменение ЧСС, АД) в течение 6 минут, регистрируя каждые 30 сек измеряемые величины. Полученные yi (12 измерений) и будут марковскими параметрами, используя которые можно построить модели (1) или (3), т.е. получить адекватную математическую модель исследуемого "черного ящика".
Итак, установив соотношение между входными (U) и выходными (yi) величинами, мы получаем метод изучения БДС в СР с использованием ММР [2,3]. Динамика поведения БДС после возмущающего воздействия при условии исходного нахождения в стационарном режиме может исследоваться и методом наименьших квадратов, когда находится не ДУ, а сразу выходная функция у=у(х). Метод наименьших квадратов подробно описан в работе [3].
Остановимся более подробно на особенностях выполнения работы. В качестве конкретных БДС выбираем ССС (тест описан выше) и респираторную систему (РС) [2]. Для последней в качестве Ui задаем гиперкапический стимул (дыхание 1% смесью CO2 и воздуха- в течение 10 сек- 5 вздохов). Наблюдаемые yi-это ЧСС, АД (max и min), частота дыхания. По регистрируемым yi строится модель ССС и РС в виде дифференциальных уравнений и производится сравнение результатов вычисления собственных значений матрицы A линейных приближений для разных испытуемых [1]. Делается вывод об идентичности или различии в системах регуляции ЧСС, АД и РС для разных моделей.
Желательно обследовать пять человек по методике представленной выше. В качестве примера приведем результаты опытов с испытуемым N. После нагрузки в период восстановления ЧСС были получены данные (см. табл.2), которые обрабатывались с использованием программы ММР. Конкретный пример такой обработки приведен в таблице 3.
Анализ результатов производился с учетом следующих замечаний: реакцию на пробу определяют по самочувствию пациента, ЧСС, АД, дыханию и данным ЭКГ как во время нагрузки, так и в восстановительный период. В институте сердечно-сосудистой хирургии АМН СССР выделены следующие типы реакции АД и ЧСС при фиксированной физической нагрузке (см. табл. 4).
Нормальной реакцией считается увеличение систолического АД на 15-30% и уменьшение диастолического АД на 10-30% или его неизменность по сравнению с исходным. Увеличение пульсового давления должно быть в тех же пределах, что и ускорение пульса. Уменьшение пульсового давления считается неадекватной реакцией АД на физическую нагрузку.
Таблица 4
| ТИП РЕАКЦИИ | ИЗМЕНЕНИЯ ЧСС И АД |
| НОРМОТОНИЧЕСКИЙ | Увеличение ЧСС соответствует приросту пульсового давления, при этом диастолическое АД не меняется. |
| ГИПОТОНИЧЕСКИЙ | Увеличение ЧСС может достигать 120-150%, а пульсовое давление возрастает лишь на 12-25% или уменьшается |
| ГИПЕРТОНИЧЕСКИЙ | Резкое повышение систолического АД до 160-180 мм рт.ст., диастолического АД до 90-100 мм рт.ст., увеличение ЧСС |
| ДИСТОНИЧЕСКИЙ | Большие сдвиги систолического и диастолического АД (появление "бесконечного тона"), резкое увеличение ЧСС |
| СТУПЕНЧАТЫЙ | На 2-3-й минуте восстановительного периода систолическое АД выше, чем на 1-й минуте |
Таким образом, тест с 30-ю приседаниями является наиболее простым, физиологичным, доступным для обследуемых любого возраста и любой трудоспособности. Он не требует специальных навыков, дорогостоящего оборудования, его интенсивность легко регулируется скоростью приседаний.
В группу лиц с повышенным АД входят дети с САД или ДАД, превышающими значения 95% от исходных точек распределения (о тенденции можно говорить при значениях выше 50-75%), в группу с пониженным АД-с САД, попадающим в нижние 5% кривой распределения (тенденция- ниже 25%). Отметим, что в норме на плечевых артериях разница АД не должна быть более 10 мм рт.ст.; на ногах АД на 20-30 мм рт. ст. выше, чем на руках.
Восстановительный период после физической нагрузки оценивают по времени и характеру восстановления ЧСС и АД. У здоровых детей пульс должен восстановиться на 5-7-й минуте, систолическое АД– на 4-5-й минуте, диастолическое АД- на 2-4-й минуте. По комплексу показателей выделяют типы реакции: а) хорошая (адекватная)- без жалоб на изменения ЧСС и АД, восстановительный период до 5 мин; б) удовлетворительная (неадекватная)- возрастание ЧСС и АД выше допустимого уровня, увеличение числа дыханий, восстановительный период до 7 мин; в)неудовлетворительная (патологическая) -выраженные отклонения ЧСС и АД, тахипноэ, ишемические изменения на ЭКГ, жалобы, восстановительный период до 10 мин и больше.
Исследования в рамках National Health Examination [2] показали, что важное прогностическое значение в отношении повышения АД у взрослых имеет масса тела в детстве (Harlan W. et al.,1979). Авторы приходят к выводу, что снижение массы тела в детстве может обеспечить надежное и эффективное предупреждение гипертензии у взрослых [2].
Многофакторный анализ, проведенный на основании данных Международного кооперативного исследования по ювениальной артериальной гипертонии, показал, что длина, масса тела и ЧСС являются наиболее значимыми независимыми переменными, вносящими вклад около 20% в вариацию уровня САД как у мальчиков, так и у девочек.
Анализируя экспериментальные данные можно наблюдать изменения в СР ССС и РС у одних и тех же людей в зависимости от эмоционального состояние или динамики рабочего дня.
Приложение 1
Для изучения устойчивости стационарных состояний без оценки в явном виде функциональных зависимостей измеряемых величин от времени широко применяется изображение зависимостей вход-выход на фазовой плоскости (ФП). Записывают функциональную зависимость от времени измеряемых величин, а потом проводят преобразование уравнений с целью получения прямых зависимостей входных величин от выходных, например, разделив одно уравнение на другое. Если первоначально мы имели пару уравнений
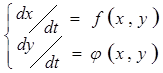
то после деления, мы получим уравнение 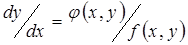 . Такая обработка особенно удобна, когда приходится анализировать зависимости, выраженные нелинейными дифференциальными уравнениями.
. Такая обработка особенно удобна, когда приходится анализировать зависимости, выраженные нелинейными дифференциальными уравнениями.
Состоянию системы соответствует точка на фазовой плоскости, которую называют изображающей. Любая динамическая система может быть приведена в состояние покоя, в котором она может находиться достаточно продолжительное время; тогда на фазовой плоскости ей соответствует особая точка. Процесс движения на фазовой плоскости изображается фазовой траекторией. Вопрос при исследовании ОТ обычно ставится так: насколько состояние покоя устойчиво и естественно для этой системы. Если существует сколь угодно малая окрестность точки покоя, что бы в ответ на возмущения в системе запускались процессы возвращающие систему в точку покоя, говорят об устойчивой точке покоя (фазовые траектории входят в особую точку). Наоборот, если при сколь угодно малых отклонениях все процессы в системе приводят у увеличению этих отклонений, то точка неустойчива (фазовые траектории выходят из особой точки).
Все процессы на фазовой плоскости могут изображаться следующими траекториями, в зависимости от значения собственных значений матрицы для данной системы.
1. Узел. Собственные значения вещественны и имеют один знак: если они положительны, то узел неустойчивый, если отрицательны- узел устойчивый. Если имеем пару равных корней, то говорят о звездообразных узлах. Фазовые траектории в общем случае представляют собой кривые входящие или выходящие из особой точки, звездообразные узлы составляются пересечением двух прямых.
Таблица 5
Особые точки и траектории на фазовой плоскости
| Тип точки | Собственные значения I1,2=A1,2+iB1,2 | Фазовая траектория | |||
| A1 | B1 | A2 | B2 | ||
| Неустойчивый узел | + | + |  | ||
| Устойчивый узел | - | - |  | ||
| Седловая точка | + | - | 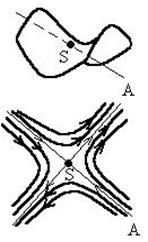 | ||
| - | + | ||||
| Устойчивый фокус | - | + | - | - | 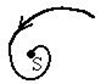 |
| Неустойчивый фокус | + | + | + | - | 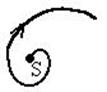 |
| Центр | + | - | 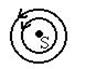 |
2. Седло. Собственные значения вещественны, но имеют различные знаки. Фазовые траектории представляют собой гиперболические кривые с двумя асимптотами, проходящими через особую точку. Асимптоты называют сепаратрисами фазовой плоскости. При движении вдоль одной из сепаратрис (АS) изображающая точка будет возвращаться в особую, все другие траектории будут уводить систему от особой точки. В таблице 5 показана трехмерная оболочка, соответствующая процессу и траектории на плоскости.
3. Фокус. Собственные значения комплексные, т.е. имеют вид I=A±iB. Если А<0, то фокус устойчивый; если А>0, то фокус неустойчивый. Фазовые траектории представляют собой спирали начинающиеся (неустойчивый) или заканчивающиеся (устойчивый) в особой точке.
4. Центр. Если корни чисто мнимые (I= ±iB), то фазовые траектории представляют собой замкнутые кривые окружающие особую точку. Движение почти устойчиво, воздействие переводит изображающую точку на соседнюю траекторию, по которой она может двигаться устойчиво до следующего воздействия.
Типы особых точек и характеристики порождающих их собственных значений перечислены в таблице 5.
Лабораторная работа № 1.3
