Е 873 Еськов В.М., Папшев В.А., Цейтлин В.А. Биофизика: Учебное пособие.

Книга предназначена для студентов биологических и медицинских факультетов университетов, изучающих курс биофизики с использованием лабораторно-практических занятий. Содержит основные разделы биофизики сложных систем и молекулярной биофизики. Может быть использована как учебное пособие для учителей школ при разработке элективных курсов биологии и физики в двенадцатилетней школе.

Рецензенты: д.п.н., профессор З.Ф. Мазур

д.б.н., профессор В.И. Попченко

ã Еськов В.М., Папшев В.А., Цейтлин В.А., 2002

ЛАБОРАТОРНАЯ РАБОТА № 1.1

БИОФИЗИКА СЛОЖНЫХ СИСТЕМ.

МОДЕЛИРОВАНИЕ ДИНАМИКИ РОСТА И РАЗВИТИЯ

ОРГАНИЗМА ЧЕЛОВЕКА – ПРИМЕР ОБРАТНЫХ СВЯЗЕЙ В ПРИРОДЕ

Цель работы:

1. Обучающийся должен знать: процессы ассимиляции и диссимиляции в клетке, примеры таких процессов в природе, вид уравнений, описывающих лимитирование процессов роста и развития, программы на ЭВМ, реализующие решения этих уравнений.

2. Обучающийся должен уметь: записать уравнение лимитирования развития популяции и динамики изменения массы отдельной сферической клетки и организма человека в целом, составить модель на ЭВМ и проанализировать получаемые результаты, уметь масштабировать графики, представляющие динамику процессов.

Практическое значение работы:

Практически все процессы в живой природе имеют лимитирующие факторы (возбуждение в нейронных сетях, численность популяций и т.д.). Каковы механизмы такого лимитирования, что такое отрицательная и положительная связь, каковы основные закономерности динамики таких процессов. Ответы на эти вопросы находятся в данной работе. Этот формализованный подход должен знать каждый биолог и медик, независимо от профиля будущей специальности, ибо это общие законы живой природы, а конкретные механизмы отрицательных обратных связей – это объект изучения исследователей в области медицины и биологии.

Оборудование:ЭВМ с принтером, карандаши, бумага

Бюджет времени:выполнение практической работы - 2 часа, самоподготовка- 2 часа, лекция- 2 часа.

ЛИТЕРАТУРА

1. Зотин А.И. Количественные теории роста.// Количественные аспекты роста.- М.: Наука, 1975.- С.267- 272.

2. Зотина Р.С., Зотин А.И. Объединенные уравнения роста.// Журнал общей биологии.- 1973.- Т. 34, №4.- С. 606- 616.

3. Рубин А.Б. Биофизика.- М.: Высшая школа.- 1987.

4. Еськов В.М., Филатова О.Е., Рачковская В.А. Лекции по экологии.- Сургут, 2000.

5. Ханин М.А. и др. Экстремальные принципы в биологии и физиологии. М.: Наука, 1978.- С.128- 146.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ

“САМОПОДГОТОВКА”

Цель этапа: 1. Повторить исходную информацию, необходимую для понимания изучаемой темы.

2. Проверить качество усвоения новой информации перед выполнением работы.

I. Исходный уровень знаний.

Для изучения темы необходимо повторить понятие лимитирования в биосистемах, основные закономерности роста и развития организмов в онто- и филогенезе, понятие математических моделей процессов, происходящих в развивающихся биологических системах.

II. Изучив блок информации и учебную литературу, обучаемый должен ответить на следующие вопросы и решить задачи:

1. Приведите пример ассимиляции в клетке (химическая реакция).

2. Приведите пример процесса диссимиляции (глюкозы, АТФ).

3. Опишите количественно процессы ассимиляции и диссимиляции веществ и объясните уравнение изменения массы клетки.

4. Приведите примеры лимитирования в природе (например, в экологии).

5. Поясните программу расчета динамики популяции с лимитированием.

6. Как осуществляется масштабирование графиков в этой работе?

7. Исходный организм (яйцо) имел размеры R= 3 см (сфера). После деления клеток при той же массе (r= 1,1 г/см³) средний размер клеток стал R= 0,01 мм. На сколько увеличилась поверхностная энергия такого организма после деления клеток, если s= 73×10³ Н/м.

Методические указания по II этапу:

“Выполнение работы”

1. Наберите представленную программу на ЭВМ. Задайте следующие начальные условия: Z0= 25 (допустимая ошибка модели); d2= 0.0001 (начальное приближение параметра лимитирования); S=20- 50 (масштаб ось у, растяжка графика на экране); DT=0.01 (масштаб времени, ось х); K=20000 (параметр цикла).

2. Определите для себя значения параметров Н0,…,НМ, с помощью программы HEIGH1.BAS идентифицируйте параметры А и В модели динамики собственного роста. Пронаблюдайте процесс построения графиков последовательного приближения, итоговый график срисуйте в тетрадь. Убедитесь в возможностях масштабирования по осям X и Y вашего графика.

Методические указания по III этапу:

“Получение зачета по лабораторной работе”.

До получения зачета по работе обучаемый должен изучить все методические указания, ответить на вопросы и решить задачи из раздела “Самоподготовка”.

После выполнения второго этапа необходимо оформить протокол работы и подписать его у преподавателя, а затем приступить к оформлению отчета в тетради.

Лабораторная работа считается зачтенной после сдачи преподавателю отчета по теоретическому и практическому разделам работы. Особое внимание следует обратить на теоретическое объяснение результатов исследований.

Блок информации

Мальтус формально был прав в 1798 году, когда говорил о возможности перенаселения планеты Земля. Однако в природе всегда существует масса лимитирующих (ограничивающих) факторов. На это еще в 19-м веке указывали ученые Ферхюльст и Пирл, предложив функциональную зависимость коэффициента скорости роста A численности X от переменной X, т.е. A=A(X). Известно, что любую функцию можно разложить в ряд по аргументу X и (если ограничиться линейным членом) получим в нашем случае A=A0–ВX (знак "-"соответствует отрицательной обратной связи). Тогда простейшая модель экспоненциального роста вида

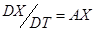(1)

примет вид:

DX/DТ=(A0-BX)X (2)

Легко видеть, что с ростом X величина A убывает и при A0-BX^*=0 или C^*=A0/B имеем DX/DT=0, т.е. скорость прироста численности равна "0". В этом случае численность популяции стабилизируется за счет отрицательных обратных связей вблизи значения X^* .

В природе роль этих обратных связей играют трофические взаимоотношения (мало пищи и A уменьшается). В популяции человека такое бывает только в слаборазвитых странах, где гибнут дети от голода и болезней в раннем возрасте. В более развитых странах роли лимитирующих факторов играют социальные условия. К ним относятся: законы государства, ограничивающие рождаемость (например, Китай); социально не престижно иметь много детей, феминистское движение, когда женщины вступают в брак и не желают иметь детей. В целом, сейчас в обществе существует масса лимитирующих факторов, обеспечивающих появление "- BX" в моделях численности популяции человека, поэтому в реальной ситуации теория Мальтуса неверна и кривая роста численности популяции человека будет иметь вид кривой с насыщением (рис.1).

Это так называемая логистическая кривая Ферхюльста- Пирла, причем для планеты Земля C^* @ 9 млрд.человек. Получить этот график Вы можете на ЭВМ, если положить в (2) DX=XN-XS и тогда

XN=XS+(A0–B*XS)*XS*DT, (3)

где знак "*" означает умножение, а XN выражается через предыдущие (старые) значения численности XS из уравнения (3). В приложении 1 приводится программа для построения и исследования графика (рис.1) зависимости Х = Х(Т) в случае действия лимитирующих факторов внешней среды.

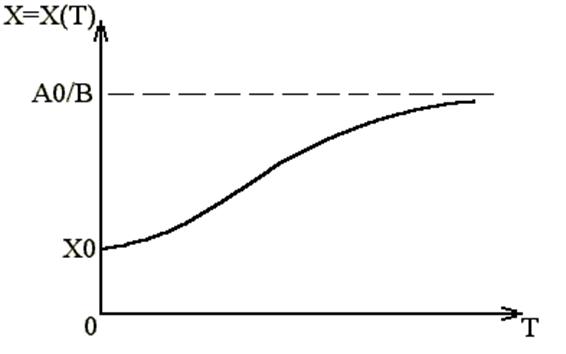
Рис. 1. Модель динамики популяции с лимитированием.

Важно отметить, что аналогичные механизмы отрицательной обратной связи функционируют и в организме человека. Действительно, человек это совокупность клеток, численность которых может быть лимитирована генетически или трофически. Следует подчеркнуть, что механизмы отрицательной обратной связи работают уже на клеточном уровне, т.к. они не дают клетке возможности расти неограниченно. Рассмотрим самый простейший случай со сферической клеткой. Известно, что поступление питательных веществ в клетку (ассимиляция веществ) происходит через её поверхность 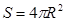, где R- радиус клетки. Ассимиляция этих веществ способствует росту клетки, увеличению её массы (и объёма) М. Одновременно с ассимиляцией происходит диссимиляция (распад) веществ. Этот процесс протекает внутри объёма клетки 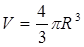и он способствует уменьшению массы вещества, т.к. побочные продукты выводятся через мембрану клетки наружу.

Таким образом динамика изменения массы (и объёма соответственно) системы зависит от двух взаимно противоположных процессов- ассимиляции и диссимиляции, т.е. можно представить, что скорость изменения М зависит от R следующим образом

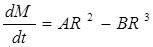. (4)

Если вспомнить, что 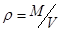(r- средняя плотность клетки, r»const), то

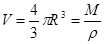и 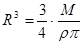. Тогда окончательно имеем, что 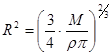и с точностью до постоянных получим

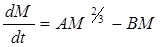. (5)

Уравнение (5) доказывает, что накопление (прибавка массы М) должно зависеть от М меньшей степени, чем диссипация (убыль массы М). Это же уравнение обосновывает и правомочность применения уравнения (2) для описания динамики массы человека, т.е.

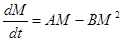. (6)

Легко видеть, что показатель степени 2/3 перешел в 1, а 1- в 2. Изменив количественно показатели, мы не изменили качественно динамику процесса- диссипация более быстрый процесс, чем ассимиляция!

Отметим, что с возрастом В может увеличиваться (постепенно), т.е. процесс распада усиливается и точка покоя М^* (dM/dt=0) уравнения (6) может уменьшить свою величину. Такая модель описывает процесс развития и старения организма человека. Отметим, что в среднем рост человека и его масса связаны приблизительно линейно (М~Н), поэтому модель для роста имеет вид уравнения (6).

В настоящей работе Вам необходимо, используя уже готовую программу, произвести идентификацию модели (найти параметры А и В) своего собственного развития. Для этого, например, надо ввести начальный рост (при рождении) Н0 (спросите у родителей), Н05 (рост в 5 лет), Н10 (рост в 10 лет), Н15 (рост в 15 лет) и НМ (текущее значение роста). Отмеченная связь роста и веса позволяет моделировать процесс исходя из величин веса в соответствующем возрасте. Рост вводим в сантиметрах, вес в килограммах. Если точной информации нет, введите данные приблизительно. Программа реализует итерационный подбор параметров модели, исходя из первичного приближения d2 (параметр лимитирования), пока расхождение между модельными данными и точками Н0,…,НМ не станет меньше ошибки Z0.

Приложение 1.

Для системы с лимитированием, описываемой уравнением

DX / DT= (A0-BX) X, (см.(3))

можно получить рекуррентное соотношение

XN = XS +(AO- B* XS)* XS* DT (7)

Программа на ЭВМ, реализующая подбор параметров этого уравнения, будет иметь вид:

CLS : SCREEN 9, 1, 0

INPUT "H0=", H0

INPUT "H05=", H10

INPUT "H10=", H20

INPUT "H15=", H30

INPUT "HM=", HM

INPUT "Z0=", Z0

INPUT "d2=", d2

INPUT "S=", S

INPUT "K=", K

INPUT "DT=", DT

CLS : LINE (40, 250)-(40, 30), 15: LINE (40, 250)-(600, 250), 15

LOCATE 3, 4: PRINT "H"

LOCATE 19, 62: PRINT "Реальное время";

10 d1 = d2 * HM

HS = H0 + (d1 - d2 * H0) * H0 * DT

FOR i = 1 TO K

HN = HS + (d1 - d2 * HS) * HS * DT

T1 = DT * i

T = 40 + i * DT * S

Y = 250 - HN * .5

PSET (T, Y), 14

IF T1 = 10 THEN P = HN

IF T1 = 20 THEN Q = HN

IF T1 = 30 THEN O = HN

IF K = 19999 THEN GOTO 100

HS = HN

NEXT i

100 Z1 = (P - H10) ^ 2 + (Q - H20) ^ 2 + (O - H30) ^ 2

Z = SQR(Z1)

IF Z > Z0 THEN d2 = d2 + .0001: GOTO 10

200 LOCATE 21, 15

PRINT "Окончательные параметры модели"

LOCATE 22, 15

PRINT "d2=", d2

LOCATE 23, 15

PRINT "d1=", d1

Программа реализует итерационный процесс расчета значений из модели и сравнения их с реальными точками Н0, Н05, Н10, Н15, НМ. Сначала задается приближение параметра лимитирования d2 достаточно малым и рассчитываются модельные результаты. В строчке 100 происходит расчет отклонения модельных данных от реального значения и сравнение с допустимой ошибкой Z0. Если отклонение больше ошибки, происходит увеличение d2 и данные рассчитываются заново с последующим сравнением; процесс идет до тех пор, пока ошибка Z0 не превысит отклонение модели. Тогда на экран выдаются параметры модели d1 (аналог А) и d2 (аналог В).

ЛАБОРАТОРНАЯ РАБОТА №1.2