В. М. Еськов, В. А. Папшев, В.А. Цейтлин

В. М. Еськов, В. А. Папшев, В.А. Цейтлин

БИОФИЗИКА

Учебное пособие для студентов заочной и очной формы обучения биологических и медицинских факультетов университетов к лабораторно-практическим занятиям

(часть 1)

Сургут, 2002 г.

УДК 376.5

ББК 74.212

Е 873

Е 873 Еськов В.М., Папшев В.А., Цейтлин В.А. Биофизика: Учебное пособие.

Книга предназначена для студентов биологических и медицинских факультетов университетов, изучающих курс биофизики с использованием лабораторно-практических занятий. Содержит основные разделы биофизики сложных систем и молекулярной биофизики. Может быть использована как учебное пособие для учителей школ при разработке элективных курсов биологии и физики в двенадцатилетней школе.

Рецензенты: д.п.н., профессор З.Ф. Мазур

д.б.н., профессор В.И. Попченко

ã Еськов В.М., Папшев В.А., Цейтлин В.А., 2002

ЛАБОРАТОРНАЯ РАБОТА № 1.1

БИОФИЗИКА СЛОЖНЫХ СИСТЕМ.

МОДЕЛИРОВАНИЕ ДИНАМИКИ РОСТА И РАЗВИТИЯ

ОРГАНИЗМА ЧЕЛОВЕКА – ПРИМЕР ОБРАТНЫХ СВЯЗЕЙ В ПРИРОДЕ

Цель работы:

1. Обучающийся должен знать: процессы ассимиляции и диссимиляции в клетке, примеры таких процессов в природе, вид уравнений, описывающих лимитирование процессов роста и развития, программы на ЭВМ, реализующие решения этих уравнений.

2. Обучающийся должен уметь: записать уравнение лимитирования развития популяции и динамики изменения массы отдельной сферической клетки и организма человека в целом, составить модель на ЭВМ и проанализировать получаемые результаты, уметь масштабировать графики, представляющие динамику процессов.

Практическое значение работы:

Практически все процессы в живой природе имеют лимитирующие факторы (возбуждение в нейронных сетях, численность популяций и т.д.). Каковы механизмы такого лимитирования, что такое отрицательная и положительная связь, каковы основные закономерности динамики таких процессов. Ответы на эти вопросы находятся в данной работе. Этот формализованный подход должен знать каждый биолог и медик, независимо от профиля будущей специальности, ибо это общие законы живой природы, а конкретные механизмы отрицательных обратных связей – это объект изучения исследователей в области медицины и биологии.

Оборудование:ЭВМ с принтером, карандаши, бумага

Бюджет времени:выполнение практической работы - 2 часа, самоподготовка- 2 часа, лекция- 2 часа.

ЛИТЕРАТУРА

1. Зотин А.И. Количественные теории роста.// Количественные аспекты роста.- М.: Наука, 1975.- С.267- 272.

2. Зотина Р.С., Зотин А.И. Объединенные уравнения роста.// Журнал общей биологии.- 1973.- Т. 34, №4.- С. 606- 616.

3. Рубин А.Б. Биофизика.- М.: Высшая школа.- 1987.

4. Еськов В.М., Филатова О.Е., Рачковская В.А. Лекции по экологии.- Сургут, 2000.

5. Ханин М.А. и др. Экстремальные принципы в биологии и физиологии. М.: Наука, 1978.- С.128- 146.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ

“САМОПОДГОТОВКА”

Цель этапа: 1. Повторить исходную информацию, необходимую для понимания изучаемой темы.

2. Проверить качество усвоения новой информации перед выполнением работы.

I. Исходный уровень знаний.

Для изучения темы необходимо повторить понятие лимитирования в биосистемах, основные закономерности роста и развития организмов в онто- и филогенезе, понятие математических моделей процессов, происходящих в развивающихся биологических системах.

II. Изучив блок информации и учебную литературу, обучаемый должен ответить на следующие вопросы и решить задачи:

1. Приведите пример ассимиляции в клетке (химическая реакция).

2. Приведите пример процесса диссимиляции (глюкозы, АТФ).

3. Опишите количественно процессы ассимиляции и диссимиляции веществ и объясните уравнение изменения массы клетки.

4. Приведите примеры лимитирования в природе (например, в экологии).

5. Поясните программу расчета динамики популяции с лимитированием.

6. Как осуществляется масштабирование графиков в этой работе?

7. Исходный организм (яйцо) имел размеры R= 3 см (сфера). После деления клеток при той же массе (r= 1,1 г/см³) средний размер клеток стал R= 0,01 мм. На сколько увеличилась поверхностная энергия такого организма после деления клеток, если s= 73×10³ Н/м.

Методические указания по II этапу:

“Выполнение работы”

1. Наберите представленную программу на ЭВМ. Задайте следующие начальные условия: Z0= 25 (допустимая ошибка модели); d2= 0.0001 (начальное приближение параметра лимитирования); S=20- 50 (масштаб ось у, растяжка графика на экране); DT=0.01 (масштаб времени, ось х); K=20000 (параметр цикла).

2. Определите для себя значения параметров Н0,…,НМ, с помощью программы HEIGH1.BAS идентифицируйте параметры А и В модели динамики собственного роста. Пронаблюдайте процесс построения графиков последовательного приближения, итоговый график срисуйте в тетрадь. Убедитесь в возможностях масштабирования по осям X и Y вашего графика.

Методические указания по III этапу:

“Получение зачета по лабораторной работе”.

До получения зачета по работе обучаемый должен изучить все методические указания, ответить на вопросы и решить задачи из раздела “Самоподготовка”.

После выполнения второго этапа необходимо оформить протокол работы и подписать его у преподавателя, а затем приступить к оформлению отчета в тетради.

Лабораторная работа считается зачтенной после сдачи преподавателю отчета по теоретическому и практическому разделам работы. Особое внимание следует обратить на теоретическое объяснение результатов исследований.

Блок информации

Мальтус формально был прав в 1798 году, когда говорил о возможности перенаселения планеты Земля. Однако в природе всегда существует масса лимитирующих (ограничивающих) факторов. На это еще в 19-м веке указывали ученые Ферхюльст и Пирл, предложив функциональную зависимость коэффициента скорости роста A численности X от переменной X, т.е. A=A(X). Известно, что любую функцию можно разложить в ряд по аргументу X и (если ограничиться линейным членом) получим в нашем случае A=A0–ВX (знак "-"соответствует отрицательной обратной связи). Тогда простейшая модель экспоненциального роста вида

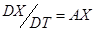(1)

примет вид:

DX/DТ=(A0-BX)X (2)

Легко видеть, что с ростом X величина A убывает и при A0-BX^*=0 или C^*=A0/B имеем DX/DT=0, т.е. скорость прироста численности равна "0". В этом случае численность популяции стабилизируется за счет отрицательных обратных связей вблизи значения X^* .

В природе роль этих обратных связей играют трофические взаимоотношения (мало пищи и A уменьшается). В популяции человека такое бывает только в слаборазвитых странах, где гибнут дети от голода и болезней в раннем возрасте. В более развитых странах роли лимитирующих факторов играют социальные условия. К ним относятся: законы государства, ограничивающие рождаемость (например, Китай); социально не престижно иметь много детей, феминистское движение, когда женщины вступают в брак и не желают иметь детей. В целом, сейчас в обществе существует масса лимитирующих факторов, обеспечивающих появление "- BX" в моделях численности популяции человека, поэтому в реальной ситуации теория Мальтуса неверна и кривая роста численности популяции человека будет иметь вид кривой с насыщением (рис.1).

Это так называемая логистическая кривая Ферхюльста- Пирла, причем для планеты Земля C^* @ 9 млрд.человек. Получить этот график Вы можете на ЭВМ, если положить в (2) DX=XN-XS и тогда

XN=XS+(A0–B*XS)*XS*DT, (3)

где знак "*" означает умножение, а XN выражается через предыдущие (старые) значения численности XS из уравнения (3). В приложении 1 приводится программа для построения и исследования графика (рис.1) зависимости Х = Х(Т) в случае действия лимитирующих факторов внешней среды.

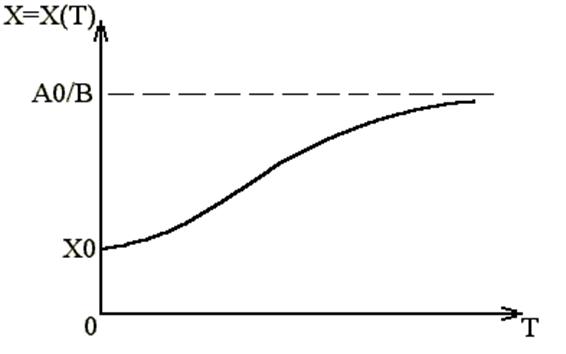
Рис. 1. Модель динамики популяции с лимитированием.

Важно отметить, что аналогичные механизмы отрицательной обратной связи функционируют и в организме человека. Действительно, человек это совокупность клеток, численность которых может быть лимитирована генетически или трофически. Следует подчеркнуть, что механизмы отрицательной обратной связи работают уже на клеточном уровне, т.к. они не дают клетке возможности расти неограниченно. Рассмотрим самый простейший случай со сферической клеткой. Известно, что поступление питательных веществ в клетку (ассимиляция веществ) происходит через её поверхность 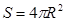, где R- радиус клетки. Ассимиляция этих веществ способствует росту клетки, увеличению её массы (и объёма) М. Одновременно с ассимиляцией происходит диссимиляция (распад) веществ. Этот процесс протекает внутри объёма клетки 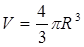и он способствует уменьшению массы вещества, т.к. побочные продукты выводятся через мембрану клетки наружу.

Таким образом динамика изменения массы (и объёма соответственно) системы зависит от двух взаимно противоположных процессов- ассимиляции и диссимиляции, т.е. можно представить, что скорость изменения М зависит от R следующим образом

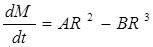. (4)

Если вспомнить, что 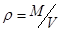(r- средняя плотность клетки, r»const), то

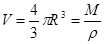и 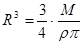. Тогда окончательно имеем, что 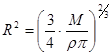и с точностью до постоянных получим

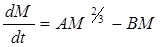. (5)

Уравнение (5) доказывает, что накопление (прибавка массы М) должно зависеть от М меньшей степени, чем диссипация (убыль массы М). Это же уравнение обосновывает и правомочность применения уравнения (2) для описания динамики массы человека, т.е.

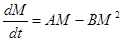. (6)

Легко видеть, что показатель степени 2/3 перешел в 1, а 1- в 2. Изменив количественно показатели, мы не изменили качественно динамику процесса- диссипация более быстрый процесс, чем ассимиляция!

Отметим, что с возрастом В может увеличиваться (постепенно), т.е. процесс распада усиливается и точка покоя М^* (dM/dt=0) уравнения (6) может уменьшить свою величину. Такая модель описывает процесс развития и старения организма человека. Отметим, что в среднем рост человека и его масса связаны приблизительно линейно (М~Н), поэтому модель для роста имеет вид уравнения (6).

В настоящей работе Вам необходимо, используя уже готовую программу, произвести идентификацию модели (найти параметры А и В) своего собственного развития. Для этого, например, надо ввести начальный рост (при рождении) Н0 (спросите у родителей), Н05 (рост в 5 лет), Н10 (рост в 10 лет), Н15 (рост в 15 лет) и НМ (текущее значение роста). Отмеченная связь роста и веса позволяет моделировать процесс исходя из величин веса в соответствующем возрасте. Рост вводим в сантиметрах, вес в килограммах. Если точной информации нет, введите данные приблизительно. Программа реализует итерационный подбор параметров модели, исходя из первичного приближения d2 (параметр лимитирования), пока расхождение между модельными данными и точками Н0,…,НМ не станет меньше ошибки Z0.

Приложение 1.

Для системы с лимитированием, описываемой уравнением

DX / DT= (A0-BX) X, (см.(3))

можно получить рекуррентное соотношение

XN = XS +(AO- B* XS)* XS* DT (7)

Программа на ЭВМ, реализующая подбор параметров этого уравнения, будет иметь вид:

CLS : SCREEN 9, 1, 0

INPUT "H0=", H0

INPUT "H05=", H10

INPUT "H10=", H20

INPUT "H15=", H30

INPUT "HM=", HM

INPUT "Z0=", Z0

INPUT "d2=", d2

INPUT "S=", S

INPUT "K=", K

INPUT "DT=", DT

CLS : LINE (40, 250)-(40, 30), 15: LINE (40, 250)-(600, 250), 15

LOCATE 3, 4: PRINT "H"

LOCATE 19, 62: PRINT "Реальное время";

10 d1 = d2 * HM

HS = H0 + (d1 - d2 * H0) * H0 * DT

FOR i = 1 TO K

HN = HS + (d1 - d2 * HS) * HS * DT

T1 = DT * i

T = 40 + i * DT * S

Y = 250 - HN * .5

PSET (T, Y), 14

IF T1 = 10 THEN P = HN

IF T1 = 20 THEN Q = HN

IF T1 = 30 THEN O = HN

IF K = 19999 THEN GOTO 100

HS = HN

NEXT i

100 Z1 = (P - H10) ^ 2 + (Q - H20) ^ 2 + (O - H30) ^ 2

Z = SQR(Z1)

IF Z > Z0 THEN d2 = d2 + .0001: GOTO 10

200 LOCATE 21, 15

PRINT "Окончательные параметры модели"

LOCATE 22, 15

PRINT "d2=", d2

LOCATE 23, 15

PRINT "d1=", d1

Программа реализует итерационный процесс расчета значений из модели и сравнения их с реальными точками Н0, Н05, Н10, Н15, НМ. Сначала задается приближение параметра лимитирования d2 достаточно малым и рассчитываются модельные результаты. В строчке 100 происходит расчет отклонения модельных данных от реального значения и сравнение с допустимой ошибкой Z0. Если отклонение больше ошибки, происходит увеличение d2 и данные рассчитываются заново с последующим сравнением; процесс идет до тех пор, пока ошибка Z0 не превысит отклонение модели. Тогда на экран выдаются параметры модели d1 (аналог А) и d2 (аналог В).

ЛАБОРАТОРНАЯ РАБОТА №1.2

Блок информации

Стационарные режимы функциональных систем организма.

Организм человека – это совокупность многих функциональных систем. Эти системы испытывают постоянные возмущения со стороны внешней и внутренней среды. Центральная нервная система (ЦНС) обеспечивает некоторую стабильность работы всех этих функциональных систем. Например, работа сердца, частота дыхания в норме приблизительно находятся около некоторого стационарного состояния. Математически это выглядит так, что скорости изменения параметров x этих систем (dx/dt) приблизительно равны нулю (т. е. dx/dt=0 или x=const).

Однако внешние возмущения приводят к dx/dt¹0. Возникает вопрос: как оценить момент, когда мы переходим от x=const к x=x(t), т.е. x¹const? Ответ на этот вопрос представлен в данной работе.

1. Понятие динамических систем в живой и неживой природе.

Любая техническая или биологическая система может быть описана некоторыми переменными величинами, которые можно трактовать как координаты некоторого вектора состояния х данной БДС, т.е.

,

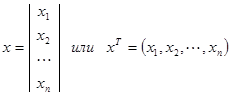где х – вектор-столбец, х^т – вектор-строка, x_i = x_i(t).

Координаты x_i(i=1,2, ... ,n) такого вектора могут иметь различный смысл. Например, для движущегося механизма x_i- это его координаты в пространстве (X,Y,Z) и во времени t, а так же величины изменения переменных (x,y,z) во времени, т.е. скорости dx/dt = V_x, dy/dt= V_y, dz/dt= V_z. Зная эти семь переменных мы можем характеризовать полностью движение любого тела в пространстве.

Отметим, что в этом примере x₁=x, x₂=y, x₃=z, x₄=V_x, x₅=V_y, x₆=V_z являются функциями (переменными) от аргумента t, т.е. вектор x=(x₁,x₂,...,x₆) состоит из 6-ти компонент. Его можно представить в виде вектора в 6-ти мерном пространстве, но графически это сделать трудно. Тем не менее мы будем говорить в дальнейшем о задании любого вектора x состояния БДС в n-мерном пространстве, которое будем называть фазовым пространством. Например, если мы имеем дело с функциональной системой (ФС) организма (по П. К. Анохину ФС – это комплекс взаимодействующих компонентов для получения полезного для организма результата), то она описывается своими переменными величинами. Одной из основных ФС человека является кардио-респираторная система (КРС), которая обеспечивает адаптивную реакцию организма на увеличение физической нагрузки или при эмоциональных стрессах. В этих случаях компонентами вектора состояния x ФС будут величины частоты сердечных сокращений (ЧСС), систолическое (САД) и диастолическое (ДАД) артериальное давление (АД), показатели электрокардиографии (ЭКГ), частоты и глубины дыхания и т.д. Все эти компоненты x_i характеризуют КРС как в покое, так и при нагрузках. Понятно, что в покое x_i»const, т.е. dx/dt»0 [3].

2. Стационарные режимы биологических динамических систем (БДС).

Их классификация.

Описание динамики поведения ФС может быть представлено в виде системы дифференциальных или разностных уравнений (ДУ и РУ), например, в виде

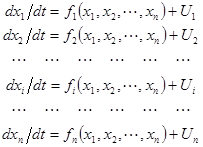, (1)

где f_i(x₁, x₂, ..., x_n)- некоторые функции, а U_i– учитывает внешние воздействия на ФС.

Отметим, что (1) можно записать в векторной форме dx/dt=Ax+U, где A является некоторой матрицей, элементы a_ij, которой представляют величины воздействия j-й компоненты вектора x на i-й компоненту. Например, модель вида

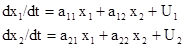(2)

имеет матрицу 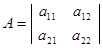, вектор x^Т=(x₁,x₂), вектор U^Т=(U₁, U₂). Она может описывать реципрокные взаимодействия в ЦНС или мышечной системе (между мышцами- агонистами, т.е. флексорами-экстензорами). Модель (2) использовалась Н.Рашевским для моделирования поведения водителя за рулем автомобиля. Важно отметить, что в стационарном состоянии (dx/dt=0) система (1) переходит в систему обыкновенных (алгебраических) уравнений, из которой можно определить координаты (x_0i) точки покоя (ТП) x₀.

Очевидно, что в биологии может быть x₀=0 (полный покой, если внешние возмущения U_i=0) или x₀>0. Например, если человек не испытывает нагрузки, то ЧСС (n) и АД (P) могут быть (x₁=n, x₂=P) постоянными, т.е. x₀₁=C₁, x₀₂=C₂.

Итак, возможны нулевые и ненулевые значения x₀. Для модели (2) x₀>0 всегда, если U>0 (докажите!). Это значит, что для открытых (с внешним драйвом) систем их стационарные состояния ненулевые. Полное описание точек покоя модели (2) и их представление на фазовой плоскости (возможны ТП типа узла, фокуса, седла и др.) представлено в приложении 1 и демонстрируется в специальном файле TPF.exe. Важно отметить, что эти ТП могут быть устойчивыми и неустойчивыми. В первом случае внешние возмущения в БДС выводят её из состояния равновесия, в которое БДС возвращается спустя некоторое время (например, устойчивый фокус). Во втором случае траектория на фазовой плоскости с течением времени уходит в бесконечность- система неустойчива.

3. Методы идентификации БДС в стационарных режимах (СР).

Итак, в стационарных режимах БДС имеет значение вектора состояний x₀=const, что очень легко идентифицировать по наблюдениям компонент x, т.е. величин x_i. Однако сама БДС может находиться в разных (внутренних) состояниях, которые можно исследовать путем предъявления на вход БДС некоторых внешних (возмущающих) стимулов (например, U_i=U_i(t)). Мы будем использовать подход "черный ящик", когда по анализу входных (U_i) и выходных (y) величин для неизвестной БДС можно построить некоторую адекватную математическую модель вида (1) или 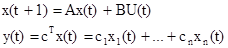(3):

(3)

Модель (3)- это модель в виде разностных уравнений, где U(t)- величина входных воздействий, B- вектор оценки U(t), c^Т- вектор- строка вклада (влияния) переменных x_i(t) на величину выхода БДС- y(t), а x(t+1) и x(t)- последующие и предыдущие значения вектора x, взятые через шаг (и интервал времени) равный 1.

В настоящей работе используется метод минимальной реализации (ММР), когда находятся модели (1) или (3) с минимальным порядком (размером вектора х) n и минимальной погрешностью P (в процентах, практически, мы требуем P < 5%). Последнее означает, что отклонение теоретических значений y_i (вычисленных из (1) или (3)) не должно превышать 5% от полученных на практике у (фактически, набор выходных величин y_i), которые называются марковскими параметрами. Используется разработанная программа, реализующая ММР для данной БДС, которая находится в линейном (или квазилинейном) состоянии. Проверить такое состояние легко. Для этого надо кратно увеличить входной стимул U и убедиться, что так же кратно увеличился сигнал y(t). Во многих случаях линейность БДС можно просто постулировать. Например, мы можем считать, что ССС в покое является линейной системой. Тогда даем нагрузку испытуемому (например, 30 приседаний за 30 сек!) и наблюдаем ответную реакцию (изменение ЧСС, АД) в течение 6 минут, регистрируя каждые 30 сек измеряемые величины. Полученные y_i (12 измерений) и будут марковскими параметрами, используя которые можно построить модели (1) или (3), т.е. получить адекватную математическую модель исследуемого "черного ящика".

Итак, установив соотношение между входными (U) и выходными (y_i) величинами, мы получаем метод изучения БДС в СР с использованием ММР [2,3]. Динамика поведения БДС после возмущающего воздействия при условии исходного нахождения в стационарном режиме может исследоваться и методом наименьших квадратов, когда находится не ДУ, а сразу выходная функция у=у(х). Метод наименьших квадратов подробно описан в работе [3].

Остановимся более подробно на особенностях выполнения работы. В качестве конкретных БДС выбираем ССС (тест описан выше) и респираторную систему (РС) [2]. Для последней в качестве U_i задаем гиперкапический стимул (дыхание 1% смесью CO₂ и воздуха- в течение 10 сек- 5 вздохов). Наблюдаемые y_i-это ЧСС, АД (max и min), частота дыхания. По регистрируемым y_i строится модель ССС и РС в виде дифференциальных уравнений и производится сравнение результатов вычисления собственных значений матрицы A линейных приближений для разных испытуемых [1]. Делается вывод об идентичности или различии в системах регуляции ЧСС, АД и РС для разных моделей.

Желательно обследовать пять человек по методике представленной выше. В качестве примера приведем результаты опытов с испытуемым N. После нагрузки в период восстановления ЧСС были получены данные (см. табл.2), которые обрабатывались с использованием программы ММР. Конкретный пример такой обработки приведен в таблице 3.

Анализ результатов производился с учетом следующих замечаний: реакцию на пробу определяют по самочувствию пациента, ЧСС, АД, дыханию и данным ЭКГ как во время нагрузки, так и в восстановительный период. В институте сердечно-сосудистой хирургии АМН СССР выделены следующие типы реакции АД и ЧСС при фиксированной физической нагрузке (см. табл. 4).

Нормальной реакцией считается увеличение систолического АД на 15-30% и уменьшение диастолического АД на 10-30% или его неизменность по сравнению с исходным. Увеличение пульсового давления должно быть в тех же пределах, что и ускорение пульса. Уменьшение пульсового давления считается неадекватной реакцией АД на физическую нагрузку.

Таблица 4

ТИП РЕАКЦИИ	ИЗМЕНЕНИЯ ЧСС И АД
НОРМОТОНИЧЕСКИЙ	Увеличение ЧСС соответствует приросту пульсового давления, при этом диастолическое АД не меняется.
ГИПОТОНИЧЕСКИЙ	Увеличение ЧСС может достигать 120-150%, а пульсовое давление возрастает лишь на 12-25% или уменьшается
ГИПЕРТОНИЧЕСКИЙ	Резкое повышение систолического АД до 160-180 мм рт.ст., диастолического АД до 90-100 мм рт.ст., увеличение ЧСС
ДИСТОНИЧЕСКИЙ	Большие сдвиги систолического и диастолического АД (появление "бесконечного тона"), резкое увеличение ЧСС
СТУПЕНЧАТЫЙ	На 2-3-й минуте восстановительного периода систолическое АД выше, чем на 1-й минуте

Таким образом, тест с 30-ю приседаниями является наиболее простым, физиологичным, доступным для обследуемых любого возраста и любой трудоспособности. Он не требует специальных навыков, дорогостоящего оборудования, его интенсивность легко регулируется скоростью приседаний.

В группу лиц с повышенным АД входят дети с САД или ДАД, превышающими значения 95% от исходных точек распределения (о тенденции можно говорить при значениях выше 50-75%), в группу с пониженным АД-с САД, попадающим в нижние 5% кривой распределения (тенденция- ниже 25%). Отметим, что в норме на плечевых артериях разница АД не должна быть более 10 мм рт.ст.; на ногах АД на 20-30 мм рт. ст. выше, чем на руках.

Восстановительный период после физической нагрузки оценивают по времени и характеру восстановления ЧСС и АД. У здоровых детей пульс должен восстановиться на 5-7-й минуте, систолическое АД– на 4-5-й минуте, диастолическое АД- на 2-4-й минуте. По комплексу показателей выделяют типы реакции: а) хорошая (адекватная)- без жалоб на изменения ЧСС и АД, восстановительный период до 5 мин; б) удовлетворительная (неадекватная)- возрастание ЧСС и АД выше допустимого уровня, увеличение числа дыханий, восстановительный период до 7 мин; в)неудовлетворительная (патологическая) -выраженные отклонения ЧСС и АД, тахипноэ, ишемические изменения на ЭКГ, жалобы, восстановительный период до 10 мин и больше.

Исследования в рамках National Health Examination [2] показали, что важное прогностическое значение в отношении повышения АД у взрослых имеет масса тела в детстве (Harlan W. et al.,1979). Авторы приходят к выводу, что снижение массы тела в детстве может обеспечить надежное и эффективное предупреждение гипертензии у взрослых [2].

Многофакторный анализ, проведенный на основании данных Международного кооперативного исследования по ювениальной артериальной гипертонии, показал, что длина, масса тела и ЧСС являются наиболее значимыми независимыми переменными, вносящими вклад около 20% в вариацию уровня САД как у мальчиков, так и у девочек.

Анализируя экспериментальные данные можно наблюдать изменения в СР ССС и РС у одних и тех же людей в зависимости от эмоционального состояние или динамики рабочего дня.

Приложение 1

Для изучения устойчивости стационарных состояний без оценки в явном виде функциональных зависимостей измеряемых величин от времени широко применяется изображение зависимостей вход-выход на фазовой плоскости (ФП). Записывают функциональную зависимость от времени измеряемых величин, а потом проводят преобразование уравнений с целью получения прямых зависимостей входных величин от выходных, например, разделив одно уравнение на другое. Если первоначально мы имели пару уравнений

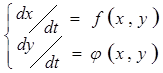
то после деления, мы получим уравнение 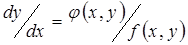. Такая обработка особенно удобна, когда приходится анализировать зависимости, выраженные нелинейными дифференциальными уравнениями.

Состоянию системы соответствует точка на фазовой плоскости, которую называют изображающей. Любая динамическая система может быть приведена в состояние покоя, в котором она может находиться достаточно продолжительное время; тогда на фазовой плоскости ей соответствует особая точка. Процесс движения на фазовой плоскости изображается фазовой траекторией. Вопрос при исследовании ОТ обычно ставится так: насколько состояние покоя устойчиво и естественно для этой системы. Если существует сколь угодно малая окрестность точки покоя, что бы в ответ на возмущения в системе запускались процессы возвращающие систему в точку покоя, говорят об устойчивой точке покоя (фазовые траектории входят в особую точку). Наоборот, если при сколь угодно малых отклонениях все процессы в системе приводят у увеличению этих отклонений, то точка неустойчива (фазовые траектории выходят из особой точки).

Все процессы на фазовой плоскости могут изображаться следующими траекториями, в зависимости от значения собственных значений матрицы для данной системы.

1. Узел. Собственные значения вещественны и имеют один знак: если они положительны, то узел неустойчивый, если отрицательны- узел устойчивый. Если имеем пару равных корней, то говорят о звездообразных узлах. Фазовые траектории в общем случае представляют собой кривые входящие или выходящие из особой точки, звездообразные узлы составляются пересечением двух прямых.

Таблица 5

Особые точки и траектории на фазовой плоскости

Тип точки	Собственные значения I1,2=A1,2+iB1,2	Фазовая траектория
A1	B1	A2	B2
Неустойчивый узел	+		+
Устойчивый узел	-		-
Седловая точка	+		-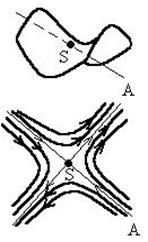
-		+
Устойчивый фокус	-	+	-	-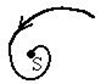
Неустойчивый фокус	+	+	+	-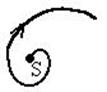
Центр		+		-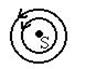

2. Седло. Собственные значения вещественны, но имеют различные знаки. Фазовые траектории представляют собой гиперболические кривые с двумя асимптотами, проходящими через особую точку. Асимптоты называют сепаратрисами фазовой плоскости. При движении вдоль одной из сепаратрис (АS) изображающая точка будет возвращаться в особую, все другие траектории будут уводить систему от особой точки. В таблице 5 показана трехмерная оболочка, соответствующая процессу и траектории на плоскости.

3. Фокус. Собственные значения комплексные, т.е. имеют вид I=A±iB. Если А<0, то фокус устойчивый; если А>0, то фокус неустойчивый. Фазовые траектории представляют собой спирали начинающиеся (неустойчивый) или заканчивающиеся (устойчивый) в особой точке.

4. Центр. Если корни чисто мнимые (I= ±iB), то фазовые траектории представляют собой замкнутые кривые окружающие особую точку. Движение почти устойчиво, воздействие переводит изображающую точку на соседнюю траекторию, по которой она может двигаться устойчиво до следующего воздействия.

Типы особых точек и характеристики порождающих их собственных значений перечислены в таблице 5.

Лабораторная работа № 1.3

Блок информации

Исследование природных экосистем- длительная и трудоемкая работа. Ее сложность еще заключается и в том, что ставить эксперименты на экосистемах опасная задача с возможностью очень тяжелых последствий для природы. Один из таких экспериментов ставит сейчас все человечество и результаты пока весьма плачевны. Вместе с тем имеется возможность реализовать желания любого исследователя- эколога не затрагивая природу. Это реализуется с помощью ЭВМ и математических моделей. В этой связи компьютерное моделирование-это весьма перспективное и безопасное направление в экспериментальной экологии и биофизике.

В рамках такого подхода уже решены многие задачи оптимального сбора урожая (отстрела животных и т. д.) в эксплуатируемых экосистемах; задачи устойчивости экосистем к неблагоприятным антропогенным воздействиям, устойчивости экологических сообществ к эпизоотиям и многие другие задачи устойчивости прикладного характера. В целом, математическая экология и теория эпидемий- весьма перспективное направление теоретической и экспериментальной биофизики популяций, а знакомство с ее методами и возможностями- необходимый элемент познания биофизики и экологии в целом.

Вместе с тем математическая экология (МЭ)- это отдельная наука со своим аппаратом, методами и обеспечением, которая использует все биологические понятия из экологии, но дает им свою специфическую трактовку. Фактически МЭ- это популяционная биофизика (ПБ) по методам исследования.

Наука начинается там, где есть математика- этот афоризм весьма уместен здесь, при изучении ПБ или математической экологии. Рассмотрение этой науки начнем с ряда задач.

1. Модель популяционного взрыва.

В природе известны эффекты резкого возрастания численности отдельных популяций, приводящие к глобальным изменениям не только экосистем, но и эколандшафтов с геологическими изменениями. Это примеры популяционных взрывов численностей леммингов на севере Скандинавии, саранчи в Африке, кроликов в Австралии и, наконец, фантастическая ситуация с “вечным хлебом” у писателя Беляева в его известном произведении. Как протекают эти процессы и каковы их закономерности? Попробуем ответить на эти вопросы с помощью математических моделей.

Пусть численность некоторого вида описывается функцией времени C=C(Т). Тогда, если предположить, что скорость DX/DT прироста численности особей X= X(T) будет зависеть от численности особей X(T) в данный момент времени, т.е.

DX/DT=AХ, (1)

где A - коэффициент скорости прироста численности особей X(T), то динамика процесса опишется функцией:

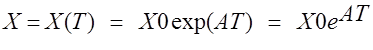, (2)

где X0- начальная численность популяции в момент времени T=T(0). Это означает экспоненциальный рост численности X со временем, т.е. X является показательной функцией от T. Посмотреть график этой зависимости на экране монитора ЭВМ Вы сможете очень просто, если воспользуетесь методом Эйлера, т.е. надо взять в качестве прироста численности DX=XN-XS (разность между наращенным (новым) значением- XN и старым значением- XS). Тогда получим рекуррентное соотношение, по которому мы вычислим последующее значение численности популяции (XN) через предыдущее значение (XS). Отметим, что это приращение DX происходит за время DT. Таким образом, если "заставить" ЭВМ выполнить в цикле последовательные итерации (расчет новых значений через старые XS) и наносить получаемые точки на экран монитора, то мы увидим зависимость X(T) в виде графика (экспоненциальной кривой), на который и указывал Мальтус в своей работе. В приложении 1 дается подробное описание программы расчета X(T) на ЭВМ в Basic, которую Вам необходимо набрать и исследовать эту зависимость для разных начальных условий (к ним относится начальная численность X и константа скорости прироста популяции A). Внешний вид этой зависимости приведен на рис.1. Из рисунка видно, что, имея меньшую начальную численность (X0₂), но большую скорость роста (A₂ ), можно быстро догнать (и перегнать) в численности другую популяцию (X0₁). В любом случае численность нарастает неограниченно и быстро.

Процессы такого вида имеют место и при росте числа раковых клеток, когда их численность в организме ничем не ограничивается и динамика процесса будет определяться только величиной коэффициента А. Облучение опухоли может резко изменить А и даже сделать А®0, что ограничит процесс развития опухоли. При этом хирургические операции могут только снизить X(T), что представляется моделью:

DX/DT = AX – M (3)

Очевидно, что при оперировании опухоли важно сделать X0=0, т.е. удалить все раковые клетки.

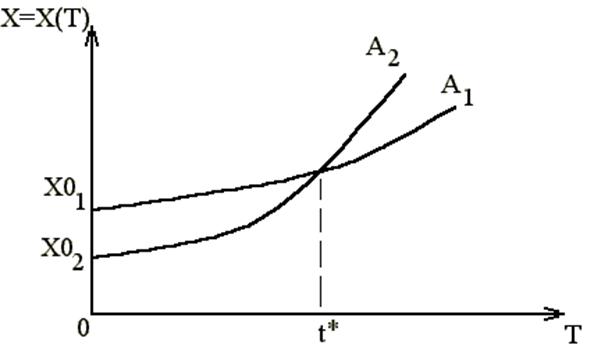
Рис. 1.Модель популяционного взрыва

Приложение 1.

В соответствии с формулой DX/DT=AX имеем, что приращение численности DX за интервал времени DT равно

DX=XN-XS=A*XS*DT (4)

Отсюда новое значение численности ХN определяется через предыдущее значение XS по формуле

XN=XS+A*XS*DT, (5)

где знак ²* ² означает умножение.

Всю программу расчета мы представим с описанием в Qbasik, при этом мы специально будем нумеровать строчки (хотя это делать и не обязательно).Итак вначале используем оператор очистки линий экрана CLS (clean line screen) и выберем тип экрана, что связано с размерами букв и числом точек, умещающихся по горизонтали (например, 640 точек) и по вертикали (360- 380, в зависимости от типа монитора). Тогда первая строка (назовем ее числом 10) имеет вид:

10 CLS: SCREEN 9, 1, 0

Здесь знак ² : ² означает разделение двух разных операций (вместо двоеточия можно поставить новую строку). Цифра 9- означает функциональный тип экрана, а 1 и 0 означает, что на черном фоне будут белые линии (буквы).

В следующей (20- ой) строке сделаем ввод в ЭВМ начальных данных условий для расчета моделей популяционного вз