Генетико-автоматические процессы в популяциях

Сопряженный дрейф генов и генетический груз.

Генетическая структура популяции может изменяться в силу случайных генетико-автоматических процессов, или дрейфа генов, которые ограничивают действие закона Харди-Вайнберга в сравнительно небольших популяциях, где всегда находятся случайные факторы, вызывающие нарушение стабильности частот аллелей, передаваемых из поколения в поколение. Величина этих нарушений находится в обратной зависимости от размера популяции, т. е., чем меньше популяция, тем сильнее проявляются отклонения фактических частот генов от ожидаемых по закону Харди-Вайнберга.

Дрейф генов ─ это изменение частоты генов в популяции в направленной или ненаправленной форме, что ведет к увеличению или к уменьшению гомозигот или гетерозигот. Он чаще всего наблюдается в изолированных популяциях при ограниченной численности её членов. Чем меньше численность особей в популяции, тем больше нарушение численного равновесия. В малых популяциях может возрастать частота нежелательного аллеля, проявляющегося в результате спаривания родственных особей.

Генетический груз – это число летальных и других отрицательных мутаций в популяции, которые при переходе в гомозиготное состояние вызывают гибель особей или снижение их жизнеспособности. Он ведет к распространению в популяции скрытых рецессивных генов и подразделяется на мутационный, сегрегационный, сбалансированный и переходный.

Мутационный груз ─ это наличие в популяции вредных генов, а также генов, в которых произошли или постоянно происходят вредные мутации. Возникает мутирование доминантного аллеля в рецессивный, что ведет к насыщению популяции рецессивными аллелями.

Сегрегационный генетический груз формируется в результате расщепления и перекомбинации аллелей при скрещивании гетерозиготных носителей старых мутаций.

Сбалансированный генетический груз обусловлен сохранением гетерозигот, что ведет к проявлению более высокой приспособленности к условиям среды.

Переходный генетический груз обусловлен тем, что адаптивный аллель утрачивает эти свойства в определенных условиях, а действие нового аллеля еще не достигло адаптивного уровня. Тогда генетический груз создается за счет присутствия исходного аллеля.

Генетический груз может играть положительную роль при искусственном отборе, т. к. является источником генетической изменчивости, способствует накоплению генотипов более приспособленных к новым факторам среды или сохранению отдельных генов за счет отбора. Генетический груз можно определить на основании фенотипического проявления мутаций в виде появляющихся уродов, врожденных аномалий и т. д,

Занятие 1. Применение закона Харди-Вайнберга.

Харди и Вайнберг провели математический анализ распределения аллелей в свободно размножающейся популяции и установили, что такая популяция находится в состоянии равновесия т.е. из поколения в поколение не изменяется и в ней сохраняется определенное соотношение генотипов, определяемое формулой.

p²AA+2pqAa+q²aa=1.

Используя приведенную выше формулу можно вычислить частоты аллелей и генотипов в тех случаях, когда доминантные гомозиготы (АА) фенотипически не отличимы от гетерозигот (Аа). С этой целью определяют процент гомозиготных по рецессивному признаку особей – q², например их оказалось 16%, после приведения к единице – 0,16. Если q²=0,16, то, можно определить q – частоту рецессивного гена – a. qa = 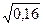=0,4. Отсюда рА=1-0,4=0,6.

На основании полученной концентрации генов определяем структуру популяции, которая равна 0,36АА + 0,48Аа + 0,16аа = 1 (р² = 0,6²; 2pq = 2 х 0,6 х 0,4; q² = 0,4²), а в процентах: 36%AA + 48%Aa + l6%aa = 100.

Определяем в популяции частоты доминантного (р) и рецессивного (q) гена.

р = 0,36 + 0,24 = 0,6

q = 0,24 + 0,16 = 0,4

Частоты аллелей остались прежними (p = 0,6; q = 0,4) и соотношение генотипов следующего поколения останется неизменным.

Далее рассмотрим, что произойдет с этой популяцией при отборе:

0,36АА + 0,48Аа + 0,16аа = 1

Бракуем особей с рецессивным признаком (0,16). Концентрация (частота) генов изменится:

р = 0,36 +0,24 = 0,6 q = 0,24 р + q = 0,6+0,24 = 0,84

Приводим концентрацию генов к единице:

0,6 : 0.84 = 0,714 0,24 : 0.84 = 0,286

Получаем следующую структуру популяции:

0,51AA + 0,408Aa +0,081aa = l

Частота доминантного аллеля в ней будет 0,714, рецессивного 0,286, то есть, структура популяции восстановится, если дальше не будем проводить, отбора.

Литература: 1,3,4.

Вид занятия: лабораторное

Место проведения –учебный класс.

Время: 2 часа.

Цель занятия: Приобрести навыки по анализу генетической структуры популяции.

Научиться определять частоты аллелей, генотипов и фенотипов в популяции.

Материальное обеспечение: таблицы, практикум, индивидуальные задания.

Содержание и методика проведения занятия.

Задание 1. Рассчитать структуру свободно размножающейся популяции при условии полного доминирования признака.

р²AA + 2pqAa +q²aa = l

Условие задачи:

q² =

q =

р = 1 – q

Задание 2. Установить, находится ли генетическая структура популяции в равновесном состоянии.

Задание 3. Определить динамику генетической структуры популяции после однократного отбора против генотипа «аа» при условии полного доминирования.

Условие задачи:

Контрольные вопросы:

1. Понятие о популяции и чистой линии.

2. Различия в эффективности отбора в популяциях и чистых линиях и их причина.

3. Генетические параметры характеризующие популяцию.

4. Генетическая структура свободно размножающейся популяции. Закон Харди-Вайнберга.

5. Закон стабилизирующего скрещивания Пирсона.

6. Основные факторы генетической эволюции в популяциях (мутации, отбор, миграции, дрейф генов, изоляция).

Подведение итогов 5 мин.