Вопрос № 17 Транспортная задача. Алгоритм метода потенциалов
Определение
Матрица С=(сij) (i= 1,m j =1,n) называется матрицей тарифов, а сами числа сij- тарифами
Определение
Планом транспортной задачи называется матрица вида Х=( хij) (i= 1,m j =1,n) в которой все элементы неотрицательные
Требуется найти значение переменных хij (i= 1,m j =1,n) обращающих в минимум целевую функцию
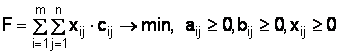
При ограничениях
Ограничения:
X11+ X12+ X1n=a1
X21+ X22+ X2n=a2 поставщика
Xm1+ Xm2+ Xmn=am
X11+ X12+ Xm1=b1
X21+ X22+ Xm2=b2 спрос потребителя
X1n+ X2n+ Xmn=bn
Xij≥0 i=1…m j=1…n
Решение:
1.Цель: минимизация расходов
2.Критерий эффективности величина расходов
3.Неуправляемые факторы: запасы поставщика и потребноть потребителя
Управляемые факторы: количество груза от поставщика к потребителю
Матрица вида Х=( хij) (i= 1,m j =1,n Называется планом транспортной задачи
4. Множество решений-множество матриц вида Х
5. ограничения по сроку потребителя и запасу поставщика
6.лпр- менеджер
Построение математической модели
Целевая функция :
Z=∑ ∑ aijxij→min 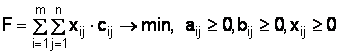
Ограничения:
X11+ X12+ X1n=a1
X21+ X22+ X2n=a2 поставщика
Xm1+ Xm2+ Xmn=am
X11+ X12+ Xm1=b1
X21+ X22+ Xm2=b2 спрос потребителя
X1n+ X2n+ Xmn=bn
Xij≥0 i=1…m j=1…n
Замечания: данная математическая модель составляется с учетом предположения что исходная задача является закрытой
Решение транспортной задачи:
Метод решения аналогичен синтетическому и представляет совокупность этапов.
1. построение опорного плана
2.проверка его на оптимальность
3.Переход от одного опорного плана к другому
Опорный план транспортной задачи.
Система ограничений вида (2) m+n уравнений и mn неизвестных → справедлива теорема:
Каждый опорный план транспортной задачи 1,2 содержит m+n базисную переменную и mn – (m+n+1) свободную переменную
Клетка соответствующая базисной переменной опорного плана называется ЗАГРУЖЕННОЙ, а клетка свободной переменной –СВОБОДНОЙ
АЛГОРИТМ:
Построение плана методом минимальной стоимости
1. загрузить в транспортную таблицу клетку с минимальным тарифом
2. исключить из рассматриваемых соответствующую поставку или потребность
3. в оставшиеся части транспортной таблицы загрузить клетку с минимальным тарифом
4. Повторить п. 2 и 3 до тех пор пока не будут исчерпаны запасы всех поставщиков , удовлетворен спрос всех потребителей
5. если в результате будет загружено m+n-1 клеток то опорный план построен. в противоположном случае все последующие клетки заполнить 0 чтобы число загруженных клеток стало (m+n-1)
Вопрос № 17 Транспортная задача. Алгоритм метода потенциалов.
Алгоритм решения транспортной задачи методом потенциалов
Алгоритм решения транспортной задачи
методом потенциалов
1. условие транспортной задачи представить в виде таблицы
2. сравнить суммарный запас всех поставщиков и Спрос всех потребителей и в случае необходимости ввести фиктивного поставщика или потребителя
3. построить опорный план методом минимальной стоимости
4. Найти потенциалы из системы уравнений ui + vj = cij, справедливых для занятых клеток. Так как занятых клеток m+n-1, то система будет состоять из m+n-1 уравнений с m+n неизвестными. Эта система имеет бесконечное множество решений. Для того чтобы найти частное решение системы, придадим одному из неизвестных любое числовое значение, например u1=0, и найдем значения остальных.
Потенциалы ui и vj записываем в столбце и в строке, которые добавляем к таблице.
5. Для всех свободных клеток найти оценки Dij= ui + vj - cij.
6. Проверка решения на оптимальность.
Если все Dij£0, то найденное решение оптимально.
Если среди оценок есть хотя бы одно положительное число, то найденное решение не оптимально и его надо улучшить.
7. Выбирается клетка с наибольшей положительной оценкой, и соответствующую переменную вводят в базис, для этого строят цикл для этой клетки.
ОПРЕДЕЛЕНИЕ:циклом называется набор клеток состоящий из2 и только 2 соседних клеток расположенных в 1-ой строке или столбце. При этом каждая клетка набора лежит в той же строке или столбце что и исходная. Среди всех клеток табл. ровно 1 клетка явл. свободной
Замечание. графиком изображения цикла является замкнутая ломаная звенья которой расположены только в строках или столбцах а все за исключением 1-ой расположены в загруженных клетках.
Алгоритм построения цикла
8 поставить в вершинах получившейся ломаной знаки + или – против часовой стрелки начиная с выбранной клетки.
9 выбрать загруженные клетки в которых стоит знак – и найти среди них наименьшее значение груза
изменить значение груза в вершинах цикла на величину l с учетом знака стоящего в клетке
повторить п.4-9
Замечание: если при отыскании оптимального планавсе оценки свободных клеток отрицательные то задача имеет единственное решение. если среди оценок свободных клеток есть хотя бы одна нулевая задача имеет бесконечное множество решений.
Замечания:
при решении транспортных задач могут возникать дополнительные условия:
· объем переходов между аi и bj заранее определен и равен а
· в этом случае вводится дополнительное ограничение xij≥a
· существует ограничение на пропускную способность т.е.объем перевозок ограничен величиной bв этом случае ограничения xij≤b
· не допускается перевозка груза из некого пункта Аi в bj в этом случае соответствующий тариф С=∞
Вопрос №18
Задача о назначениях
необходимо назначить m работников на n работ чтобы коэффициент выполнения был максимальный при условии что 1 работник выполняет только 1 работу и 1 работа может быть выполнена только 1 работником
эффективность выполнения представлена в виде таблицы.
| Работа/работники | n | |||
| а11 х11 | а12 х12 | а1n х1n | ||
| а21 х1 | а22 х2 | а2n х2n | ||
| m | аm1 хm1 | аm2 хm2 | аmn хmn |
структурирование операции:
1.цель:максимилизация суммарной эффективности всех видов работ
2.критерий эфф. величина суммарной эффективности всех видов работ
3.управляемые факторы: фактор назначения i работника на j работу
Xij=0 работник не назначен
Xij=1 работник назначен
неуправляемые факторы взаимооднозначное соответствие между количеством работников и работ
Х= (Xij)-макс закрепленных работников за работами
4.множество возможных решение –множество матриц вида Х
5.ограничения по взаимооднозначному соответствию
6. ЛПР-менеджер по управлению персоналом
Построение модели
целевая функция Z=∑ ∑ aij Xij→max (min)
max-для эффективности
min-для времени
ограничения:
X11+ X12+ X1n=1
X21+ X22+ X2n=1
Xm1+ Xm2+ Xmn=1
X11+ X21+ Xm1=1
X12+ X22+ Xm2=1
X1n+ X2n+ Xmn=1
Xij€{1,0]
