Вычисление критерия хи-квадрат

Класс

Наблюдаемые данные

Ожидаемые данные

(О – Е)

(О -- Е)2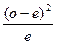

Доминантный 6023 6018 +5 25 0,0041

Рецессиный 2001 2006 —5 25 0,0124

∑=8024 ∑ = 8024 ∑=0,0165

При оценке согласия принято пользоваться тремя уровнями значимости: Р = 0,05; Р = 0,01 и Р= 0,001, для которых в приложении 2 приведены стандартные значе­ния хи-квадрат. Если вычисленное значение хи-квадрат больше стандартного, находящегося в графе Р = 0,01 и тем более в графе P=0,00l, то следует считать, что ги­потеза не согласуется с полученными в опыте данными. Если вычисленная величина хи-квадрат меньше таб­личной, находящейся в графе Р = 0,01, но больше той, которая находится в графе Р = 0,05, согласие наблюдае­мых данных с ожидаемыми является сомнительным. Од­нако это не дает права отбросить нулевую гипотезу. Ес­ли же вычисленная величина хи-квадрат меньше таб­личной графы Р = 0,05, то соответствие наблюдаемых данных с ожидаемыми считается установленным.

Величина хи-квадрат зависит от числа степеней сво­боды. Поэтому для каждого значения вероятности (Р) дано несколько значений χ², расположенных в приложе­нии 2 под определением уровнем значимости. В рас­сматриваемых нами примерах число степеней свободы (v) на единицу меньше числа классов. В опыте имеется два класса, число степеней свободы равно 1. Следовательно, для решения задачи нужно использовать изприложения 2 уровни «вероятности» и строку «v = l».

В этой строке стоят три значения хи-квадрат; 3,8; 6,6; 10,8. Вычисленное значение χ²-квадрат значительно мень­ше табличных. Следовательно, наблюдаемое в опыте расщепление соответствует ожидаемому, а поэтому ну­левая гипотеза, т. е. расщепление в соотношении 3:1, остается в силе.

Применение критерия хи-квадрат при сравнении двух эмпирических рядов.В таблице 13 приведен вариационный ряд жирномолоч­ности селекционного ядра коров белорусской черно-пестрой породы , а в ка­честве теоретических частот взят вариационный ряд пользовательного стада.