Пример расчетов при дисперсионном анализе однофакторных комплексов для малых групп

	Градации изучаемого фактора --типы конституций	Число градаций
грубый	нежный	плотный	рыхлый

Варианты 2 2 2 2

(число ягнят) 2 2 2 1

х 1 2 2 1

1 1 3 2

2 2 2 1

Число

вариант n_i 5 5 5 5 N = n_i=20

∑x_i 8 9 13 7 ∑x_ij=37

∑(x_i)² 64 81 169 49 ∑(∑x_i)=368

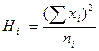12,8 16,2 38,8 9,8 ∑H_i=72,6

∑x² _I 14 17 35 11 ∑x² _I=77

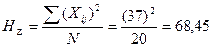
Для получения строки Hi производят деление чисел предыдущей строки на число вариант соответствующей градации 64:5=12,8,

81 :5 и т. д., после чего, суммируя их, получают сумму H_i-= 72,6. Для получения сумм квадратов вариант (∑x_i)² нужно поочередно возвести в квадрат H каждую варианту соответствующей града­ции и полученные квадраты суммировать ∑x²_I =2²+2²++1²+1² +2² =14 и т. д. Сложив числа этой строки, по­лучаем ∑x²_i.j Наконец, для вычисления H_∑ сумму ва­риант (Zx_ij) надо возвести в квадрат и разделить на общее число вариант.

Мерой разнообразия признака при однофакторном дисперсионном анализе используются дисперсии:

С_у — общая дисперсия — сумма квадратов центральных отклонений признака (плодовитости овец) вычисляется по формуле:

C_y=∑x²_ij — H_∑ (40)

C_{x --} факториальная (межгрупповая) дисперсия, харак­теризую-щая влияние изучаемого фактора (типа консти­туции овец), по формуле:

C_х=∑ Н_i — H_∑ (41)

С_∑ — случайная, остаточная (внутригрупповая) дисперсия, обусловленная влиянием всех других факторов, вычисляется по формуле:

C_∑=∑x²_{i j} — ∑H_i

Величины дисперсий составляют: С_у =77—68,45 =8,55; С_х=72,6 —68,45=4,15; С_∑ = 77—72,6 = 4,4.

Таким образом, показатель общего разнообразие (Су) разложен на два составляющих компонента: разнообразие, зависящее от изучаемого фактора (типа конституции овец — С_х), и разнообразие, зависящее от совокупности других факторов (С_∑). При этом, конечно, С_у=С_х+С_г. В данном примере 8,55 = 4,15+4,4 (целесообразно сделать подсчет для проверки правильности вычислений).

Для оценки доли общего разнообразия признака обусловленной изучаемым фактором (типом конституции овец), вычисляют отношение факториальной дисперсии к общей дисперсии. Это отношение обозначается символом η_х ².

η_х ² =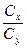

В разбираемом примере С_х : С_у = 4,15 : 8,55 = 0,49
Следовательно, типом конституции обусловлено 49% общего разнообразия плодовитости овец.

Дисперсионный анализ позволяет оценить достоверность
выводов. Для этого применяются три способа :вычисление средней ошибки силы влияния (т_η), вычисление показателя достоверности влияния по Фишеру (F)вычисление показателя Ө— (показатель достоверности влияния по Н. А. Плохинскому). Третий, наиболее простой способ заключается в следующем: по данным опыта вычисляют эмпирический показатель Ө и сравнивают его со стандартным значением этого показателя (Ө_st) свидетельствующим о достоверности вывода с вероятностью 0,95. Стандартные значения Ө_st приведены в приложении 3. Вычисление эмпирического показателя достоверности производится по формуле:

θ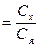

Чтобы найти стандартное значение Ө_st, нужно определить число степеней свободы (v). Для С_х число степеней свободы v = r-1 (на единицу меньше числа града­ций фактора х).

Для С_г число степеней свободы равно общему числу вариант, уменьшенному на число градаций фактора: V_{2 =} N—r. Стандартное значение Ө_st нужно найти в при­ложении 3 на перекрестке графы v_i и строки v₂.

В рассматриваемом примере эмпирическое значение Ө = C_X; С_z = 4,15: 4,4 = 0,94; степени свободы равны: v₁ = 5 -1=4; v₂ =20—5=15. По приложению 3 находим: Ө_st = 0,82 (среднее между 0,89 и 0,75). Эмпирическое значение Ө в данном случае выше стадартного, что сви­детельствует о его достоверности с вероятностью более 0,95.

Определение наследуемости в однофакторном дисперсионном комплексе. Требуется определить наследуемость жирномолочности в потомстве трех быков-производителей: Луча, Ветра, Алмаза. Для этого составляют однофакторный диспер­сионный комплекс (табл. 16), в градации которого за­писываются показатели жирномолочности дочерей бы­ков.

Подсчитывают сумму вариант ∑_х по графам таблицы, определяют средние арифметические величины в группе дочерей каждого быка Xi; 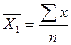и во всей выборке: . Затем определяем дисперсию — сумму квадратов: 1

генетическую дисперсию С_vС_x — межгрупповую Сумму квадратов – показатель генетического разнообразия жирномолочности родителей по формуле:

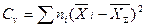(45)

Су = 5 (+0,25)² +5 (—0,05)² +5 (— 0,21)² = 0,5455;