Сравнение эмпирического и теоретического

Вариационных рядов методом хи-квадрат

Класс

Наблюдаемые данные (О)

Ожидаемые данные (Е)

(О – Е)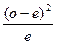

3,5 1} 3 -- 3 9:8=1,12

3,8 4} 5

4,1 5 10 -- 5 25:10=2,50

4,4 7 11 -- 4 16:11=1,45

4,7 10 9 + 1 1:9=0,11

5,0 17 7 +10 100:7=14,30

5,3 4} 3

5,6 2} 2 +1 1: 5=0,20

Итого 50 50 ∑ =19,63

Требуется определить, достоверны ли различия по жирномолочности кавказских буйволиц разных групп. В качестве нулевой гипотезы примем предположе­ние о том, что между селекционной и пользовательной частями стада различий не имеется. Если число наблю­дений в классах меньше 5, то такие частоты смежных классов объединяют. Таким образом, получено 6 клас­сов (l) χ²= 19,68. Находим число степеней свободы: v= = l—2 = 6—2 = 4. При v, равном 4, и Р, равном 0,01, стандартное значение хи-квадрат равно 13,3. Следова­тельно, нулевая гипотеза, т. е. предположение о том, что различий между пламенным ядром и пользовательным стадом нет, отвергается.

Применение критерия хи-квадрат при определении достоверности различиймежду двумя группами ж и тн ых. Предположим, что требуется оценить результат испытания нового препарата для предупреждения инфекционного заболевания кроликов.

Из 50 кроликов 20 получали профилактический препарат (опытная группа), а 30 не получали (контроль). В опытной группе заболело 7 особей, здоровыми остались 13. В контро-льной заболело 14 кроликов, остались здоровыми 16. Доказывают ли результаты опыта профилактическое действие препарата или различие в числе заболевших кроликов зависит не от введения препа­рата, а от случайных причин. Обработка материала приведена в таблице 14.

Расчет критерия хи-квадрат при определении достоверности