Сверху свободно снизу свободно

Вверх вниз влево вправо.

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

Сверху свободно снизу свободно

слева свободно справа свободно

A	B	C	D	E	F

Цикл

ПОКА < условие >

Последовательность команд

КОНЕЦ ПОКА

выполняется, пока условие истинно. В конструкции

ЕСЛИ < условие >

ТО команда1

ИНАЧЕ команда2

КОНЕЦ ЕСЛИ

выполняется команда1 (если условие истинно) или команда2 (если

условие ложно).

Если РОБОТ начнёт движение в сторону находящейся рядом с ним

стены, то он разрушится и программа прервётся.

Сколько клеток лабиринта соответствуют требованию, что, начав

движение в ней и выполнив предложенную программу, РОБОТ уцелеет

и остановится в закрашенной клетке (клетка F6)?

1) 8 2) 15 3) 24 4) 27

НАЧАЛО

ПОКА < справа свободно ИЛИ снизу свободно >

ПОКА < справа свободно >

Вправо

КОНЕЦ ПОКА

ПОКА < снизу свободно >

Вниз

КОНЕЦ ПОКА

КОНЕЦ ПОКА

КОНЕЦ

Решение:

1) обратим внимание, что в программе три цикла, причем два внутренних цикла вложены в один внешний

2) цикл

ПОКА < справа свободно >

Вправо

КОНЕЦ ПОКА

означает «двигаться вправо до упора», а цикл

ПОКА < снизу свободно >

Вниз

КОНЕЦ ПОКА

означает «двигаться вниз до упора»

3) тогда программу можно записать в свободном стиле так:

ПОКА не пришли в угол

Двигаться вправо до упора

Двигаться вниз до упора

КОНЕЦ ПОКА

где угол – это клетка, в которой есть стенки снизу и справа

4) за каждый шаг внешнего цикла Робот проходит путь в виде «сапога», двигаясь сначала вправо до упора, а затем – вниз до упора:

→	→	↓
		↓
		↓

клетка, выделенная красным фоном особая – в ней заканчивается один шаг внешнего цикла и начинается следующий:

а) Робот может попасть в эту клетку, двигаясь вниз из клетки, где справа – стенка

б) снизу есть стенка;

в) снизу стенка есть, справа – нет, поэтому будет выполнен еще один шаг внешнего цикла.

5) в клетку F6 (это угол, где Робот остановился), Робот мог придти за один шаг внешнего цикла (за один «сапог») только из отмеченных клеток:

→	→	→	→	→	↓
			→	→	↓
→	→	→	→	→
A	B	C	D	E	F

6) теперь отметим красным фоном особые клетки, которые удовлетворяют условиям а-в пункта 4 (см. выше), их всего 2:

→	→	→	→	→	↓
			→	→	↓
→	→	→	→	→
A	B	C	D	E	F

7) отметим все пути в форме «сапога», которые приводят в особые клетки:

→	→	↓
→	→	↓
→	→	→	→	→	↓
→	→	↓	→	→	↓
→	→	→	→	→
A	B	C	D	E	F

8) больше особых клеток (см. пункт 4) нет; всего отмечено 24 клетки (считая конечную клетку F6)

9) таким образом, правильный ответ – 3.

Возможные ловушки и проблемы: · нужно помнить, что внешний цикл может выполняться более одного раза; неучет этого обстоятельства приводит к неверному ответу 2 (15 клеток) · важен порядок выполнения внутренних циклов (в данном случае сначала Робот идет вправо, а затем – вниз); при изменении этого порядка изменится и результат, в частности, изменятся условия, определяющие особую клетку

Еще пример задания:

A	B	C	D	E	F

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:

Вверх вниз влево вправо.

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

Сверху свободно снизу свободно

слева свободно справа свободно

Цикл ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку. Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?

1) 1 2) 2 3) 3 4) 0

НАЧАЛО

ПОКА <снизу свободно> вниз

ПОКА <слева свободно> влево

ПОКА <сверху свободно> вверх

ПОКА <справа свободно> вправо

КОНЕЦ

Решение:

10) легко понять, что для того, чтобы исполнитель вернулся обратно в ту клетку, откуда он начал движения, четыре стенки должны быть расставлены так, чтобы он упирался в них сначала при движении вниз, затем – влево, вверх и, наконец, вправо:

на рисунке красная точка обозначает клетку, начав с которой РОБОТ вернется обратно;

11) кроме этих четырех стенок, необходимо, чтобы коридор, выделенный на рисунке справа зеленым фоном, был свободен для прохода

12) обратим внимание, что возможны еще «вырожденные» варианты, вроде таких:

13) итак, мы выяснили, что нужно рассматривать лишь те клетки, где есть стенка справа; отметим на исходной карте клетки-кандидаты:

		·			·
				·	·
					·
					·
	·				·
·					·
A	B	C	D	E	F

					·
					·
					·
					·
					·
					·
A	B	C	D	E	F

14) этих «подозрительных» клеток не так много, но можно еще сократить количество рассматриваемых вариантов: если РОБОТ начинает движение с любой клетки на вертикали F, он все равно приходит в клетку F4, которая удовлетворяет заданному условию, таким образом, одну клетку мы нашли, а остальные клетки вертикали F условию не удовлетворяют:

15) проверяем оставшиеся четыре клетки-кандидаты, но для каждой из них после выполнения алгоритма РОБОТ не приходит в ту клетку, откуда он стартовал:

		·
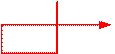A	B	C	D	E	F

	·
A	B	C	D	E	F

				·
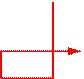A	B	C	D	E	F

·
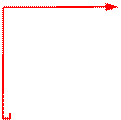A	B	C	D	E	F

16) итак, условию удовлетворяет только одна клетка – F4

17) таким образом, правильный ответ – 1.

Возможные ловушки и проблемы: · вариантов может быть достаточно много, важно не пропустить ни один из них · можно попытаться выполнить алгоритм для каждой клетки лабиринта, но это займет много времени; поэтому лучше ограничиться только клетками-кандидатами · нужно правильно определить свойства, по которым клетку можно считать «кандидатом» · можно не заметить стенку и таким образом получить лишнее решение

Еще пример задания:

A	B	C	D	E	F

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:

Вверх вниз влево вправо.

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

сверху свободно снизу свободно

слева свободно справа свободно

Цикл ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку. Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ уцелеет (не врежется в стену) и остановится в той же клетке, с которой он начал движение?

1) 1 2) 2 3) 3 4) 0

НАЧАЛО

ПОКА <слева свободно> вверх

ПОКА <сверху свободно> вправо

ПОКА <справа свободно> вниз

ПОКА <снизу свободно> влево

КОНЕЦ

Решение:

1) особенность этой задач в том, что РОБОТ проверяет стенку в одном направлении, а движется в другом

2) рассмотрим первый цикл:

ПОКА <слева свободно> вверх

понятно, что при движении вверх РОБОТ остановится в первой же клетке, где слева будет стена

3) рассуждая аналогично, находим, что во втором цикле при движении вправо РОБОТ останавливается в клетке, где есть стена сверху; в третьем цикле (движение вниз) РОБОТ останавливается в клетке, где есть стена справа;

4) наконец, в четвертом цикле РОБОТ останавливается в клетке, где есть стена снизу; при этом он должен попасть обратно в исходную клетку, обозначенную на рисунке красной точкой;

5) кроме этих четырех стенок, необходимо, чтобы коридор, выделенный на рисунке зеленым фоном, был свободен для прохода, иначе РОБОТ врежется в стенку

6) теперь отметим на карте все клетки-кандидаты, где снизу есть стена:

				·
	·
					·
		·
·	·	·	·	·	·
A	B	C	D	E	F

7) при движении из клеток B5, D1, E1, E6, F1 и F3 РОБОТ врежется в стенку, потому что слева стены нет и условие «слева свободно» всегда истинно:

				·
	·
					·
		·
·	·	·	·	·	·
A	B	C	D	E	F

8) начав движение с клетки A1, C1 или C2, РОБОТ также врезается в стенку и разрушается:

		·
·	·	·
A	B	C	D	E	F

9) и только путь, начатый в клетке B1, приводит РОБОТА обратно в точку старта:

	·
A	B	C	D	E	F

10) таким образом, только клетка B1 удовлетворяет условию задачи, поэтому …

11) правильный ответ – 1.

Еще пример задания:

В приведенном ниже фрагменте алгоритма, записанном на алгоритмическом языке, переменные a, b, c имеют тип «строка», а переменные i, k – тип «целое». Используются следующие функции:

Длина(a) – возвращает количество символов в строке a. (Тип «целое»)

Извлечь(a,i) – возвращает i-тый (слева) символ в строке a. (Тип «строка»)

Склеить(a,b) – возвращает строку, в которой записаны сначала все символы
строки a, а затем все символы строки b. (Тип «строка»)

Значения строк записываются в одинарных кавычках (Например, a:='дом'). Фрагмент алгоритма:

i := Длина(a)

k := 2

b := 'А'

пока i > 0

Нц

c := Извлечь(a,i)

b := Склеить(b,c)

i := i – k

Кц

b := Склеить(b,'Т')

Какое значение будет у переменной b после выполнения вышеприведенного фрагмента алгоритма, если значение переменной a было ‘ПОЕЗД’?

1) ‘АДЕПТ’ 2) ‘АДЗЕОП’ 3) ‘АДТЕТПТ’ 4) ‘АДЗОТ’

Решение:

1) эта задача более близка к классическому программированию, здесь выполняется обработка символьных строк; вся информация для успешного решения, вообще говоря, содержится в условии, но желательно иметь хотя бы небольшой опыт работы с символьными строками на Паскале (или другом языке)

2) заметим, что последняя команда алгоритма, b:=Склеить(b,'Т'), добавляет букву 'Т' в конец строки b, поэтому ответ 2 – явно неверный (строка должна оканчиваться на букву 'Т', а не на 'П')

3) для решения будем использовать ручную прокрутку; здесь пять переменных: a, b, c, i, k, для каждой из них выделим столбец, где будем записывать изменение ее значения

4) перед выполнением заданного фрагмента мы знаем только значение a, остальные неизвестны (обозначим их знаком вопроса):

	a	b	c	i	k
	'ПОЕЗД'	?	?	?	?

5) в первой команде длина строки a (она равна 5 символам) записывается в переменную i:

	a	b	c	i	k
	'ПОЕЗД'	?	?	?	?
i:=Длина(a)

6) следующие два оператора записывают начальные значения в k и b:

	a	b	c	i	k
	'ПОЕЗД'	?	?	?	?
i:=Длина(a)
k:=2
b:='А'		'A'

7) далее следует цикл пока с проверкой условия i>0 в начале цикла; сейчас i=5>0, то есть, условие выполняется, цикл начинает работать и выполняются все операторы в теле цикла:

	a	b	c	i	k
	'ПОЕЗД'	?	?	?	?
i:=Длина(a)
k:=2
b:='А'		'A'
i > 0?	да
c:=Извлечь(a,i)	i:=Длина(a)
b:=Cклеить(b,c)	k:=2
i:=i–k

· поскольку i=5, вызов функции Извлечь(a,i) выделяет из строки a символ с номером 5, это 'Д';

· следующей командой этот символ приписывается в «хвост» строки b, теперь в ней хранится цепочка 'АД';

· в команде i:=i-k значение переменной i уменьшается на k (то есть, на 2)

8) далее нужно перейти в начало цикла и снова проверить условие i>0, оно опять истинно, поэтому выполняется следующий шаг цикла, в котором к строке b добавляется 3-й символ строки a, то есть 'Е':

	a	b	c	i	k
...	'ПОЕЗД'	'АД'	…
i > 0?	да
c:=Извлечь(a,i)			'Е'
b:=Cклеить(b,c)		'АДЕ'
i:=i–k

9) условие i>0 истинно, поэтому тело цикла выполняется еще один раз, к строке b добавляется 1-й символ строки a, то есть 'П':

	a	b	c	i	k
...	'ПОЕЗД'	'АДЕ'	…
i > 0?	да
c:=Извлечь(a,i)			'П'
b:=Cклеить(b,c)		'АДЕП'
i:=i–k				–1

10) теперь i=-1, поэтому при очередной проверке условие i>0 в начале цикла оказывается ложным, выполнение цикла заканчивается, и исполнителю остается выполнить единственную строчку после цикла, которая дописывает в конец строки b букву 'Т':

	a	b	c	i	k
...	'ПОЕЗД'	'АДЕП'	…	–1
i > 0?	нет
b:=Склеить(b,'Т')		'АДЕПТ'

11) у нас получилось, что в конце выполнения фрагмента алгоритма в переменной b будет записана последовательность символов 'АДЕПТ'

12) таким образом, правильный ответ – 1.

Возможные проблемы: · таблица получилась достаточно громоздкая, однако она позволяет наиболее наглядно решить задачу

Еще пример задания[1]:

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:

Вверх вниз влево вправо.

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: