Краткие теоретические сведения. Многофакторный дисперсионный комплекс – это совокупность исходных наблюдений, позволяющих статистически оценить действие и взаимодействие нескольких изучаемых

Многофакторный дисперсионный комплекс – это совокупность исходных наблюдений, позволяющих статистически оценить действие и взаимодействие нескольких изучаемых факторов на изменчивость результативного признака. Эффект взаимодействия составляет ту часть общего варьирования, которая вызвана различным действием одного фактора при разных градациях другого. Специфическое действие сочетаний в эксперименте выявляется тогда, когда при одной градации первого фактора второй действует слабо или угнетающе, а при другой градации он проявляется сильно и стимулирует развитие результативного признака.

Дисперсионный анализ данных многофакторного комплекса проводится в два этапа. Первый этап – разложение общей вариации результативного признака на варьирование вариантов и остаточное: 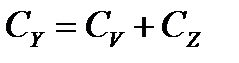. На втором этапе сумма квадратов отклонения для вариантов разлагается на компоненты, соответствующие источникам варьирования – главные эффекты изучаемых факторов и их взаимодействия.

В двухфакторном опыте:

.

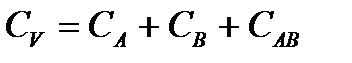В трехфакторном:

.

Дисперсионный анализ двухфакторного анализа по изучению градаций фактора А (число вариантов l_A) и градаций фактора В (число вариантов l_B), проведенного в n повторностях, осуществляется в следующие этапы:

1 Определяются суммы и средние по вариантам, общая сумма и средний урожай по опыту.

2 Вычисляются общая сумма квадратов отклонений, сумма квадратов для вариантов и остатка: ;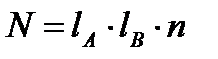

;

;

;

.

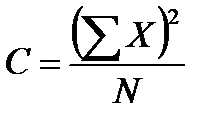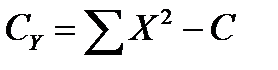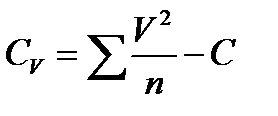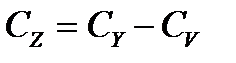Для вычисления сумм квадратов по факторам А, В и взаимодействию АВ составляется вспомогательная таблица, в которую записываются суммы по вариантам. Суммируя цифры, находятся суммы А, суммы В и вычисляются суммы квадратов отклонений для главных эффектов и взаимодействия.

Сумма квадратов для фактора А:

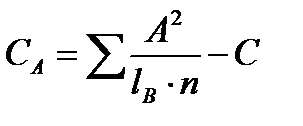при (l_А – 1) степенях свободы.

Сумма квадратов для фактора В:

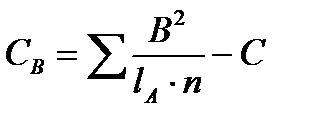при (l_В – 1) степенях свободы.

Сумма квадратов для взаимодействия АВ находится по разности:

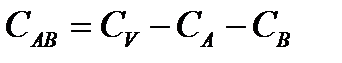при (l_А – 1)×(l_В – 1) степенях свободы.

При дисперсионном анализе ортогональных комплексов используются аддитивные свойства частных дисперсий (сумм квадратов центральных отклонений).

Если взять отношения частных сумм квадратов к общей:

;

.

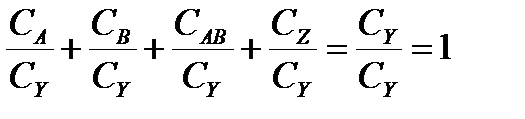Каждое из этих отношений будет показывать долю участия отдельной частной дисперсии в образовании общей дисперсии. А так как каждая частная сумма квадратов соответствует одному из частных влияний, то отношение частной суммы квадратов к общей измеряет долю данного влияния в общем суммарном статистическом влиянии всех факторов, определяющих развитие данного результативного признака.

Поэтому доля (выраженная в относительных единицах или в процентах) каждой частной дисперсии в общей их сумме может быть принята за показатель силы влияния, того влияния, которое характеризуется данной частной дисперсией – или одной из факториальных или случайной.

Таким образом, сила влияния фактора (факторов) в дисперсионном анализе измеряется отношением дисперсий частных к общей:

.

Так как этот показатель отражает основной закон разложения общих дисперсий и основное аддитивное свойство частных дисперсий, а также составлен из основных элементов дисперсионного анализа, то
отношение одной из факториальных дисперсий (С_V, С_А, С_B, С_АB) или случайной дисперсии (C_Z) к общей (С_Y) можно назвать основным показателем силы влияний факторов – организованных и неорганизованных.

Проведение анализа

На 12 опытных делянках проводились экспериментальные работы с посевом кормовых злаковых трав. Факторы a и b отражают объективную ситуацию в процессе проведения опыта (a – освещенность и b – увлажнение) или фактор среды (неорганизованный фактор). Факторы о и р – факторы влияния: о – фоновые, без внесения удобрений, р – с внесением (организованный фактор). Результативным признаком является урожайность. Исходные данные, представленные в таблице 13.1 использовались для выполнения двухфакторного дисперсионного анализа.

Следует отметить, что в проведении анализа в табличном редакторе MS Excel количество повторений (факторы о и р) должно быть одинаковым. В данном случае 3. Для выполнения подобного анализа в программном продукте Statistica 6 количество повторений может быть разновеликим.

Таблица 13.1 – Исходные данные

	a	b
o
o
o
p
p
p

Шаг 1. Откройте модуль Анализ данных выберите опцию Двухфакторный дисперсионный анализ с повторениями, после чего щелкните мышкой OK.

Шаг 2. В появившемся окне выполнить операции и установки, как показано на рисунке 13.1. Щелкнуть мышкой OK.

Шаг 3. Результат обработки появится в указанном поле (выходной интервал $D$1, таблицы 13.2, 13.3).

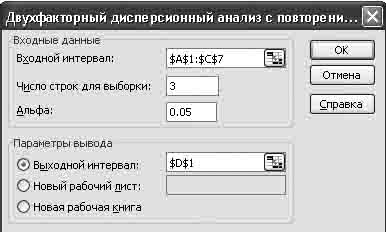
Рисунок 13.1 – Стартовая панель

Таблица 13.2 – Статистические параметры

	a	b	Итого
o
Счет
Сумма
Среднее	60,33	50,67	55,5
Дисперсия	510,33	14,33	237,9
p
Счет
Сумма
Среднее	69,33	77,67	73,5
Дисперсия	21,33	40,33	45,5
Итого
Счет
Сумма
Среднее	64,83	64,17
Дисперсия	236,97	240,57

Таблица 13.3 – Дисперсионный анализ

Источник вариации	SS	df	MS	F	P-значение	F крит.	Сила влияния, %
Выборка (2 фактор)				6,63	0,035	5,32	40,7
Столбцы (1 фактор)	1,33		1,33	0,0091	0,93	5,32	0,1
Взаимодействие				1,658	0,23	5,32	10,2
Внутри	1172,67		146,58				49,0
Итого

В рассмотренном примере F-критерий показывает, что нулевая гипотеза отвергается и различие между средними статистически значимо за счет влияния второго фактора (значимо на уровне 0,033, что не превышает критического уровня 0,05). Сила влияния этого фактора составляет около 41%. В свою очередь, по первому фактору и взаимодействию обоих факторов нулевая гипотеза о равенстве средних не отвергается, поскольку критерий Фишера меньше табличного значения и уровень значимости р > 0,05. Поэтому, в данном случае прибавка к урожаю обусловлена только организованным фактором.

Задания для выполнения

1 Введите в таблицу MS Excel исходные данные из Приложения Е (таблица Е1).

2 Выполните расчетные процедуры в соответствии с порядком операций, выполненных в настоящем разделе.

Получите результат и сделайте заключение.

Лабораторная работа 14
Многофакторный дисперсионный анализ (многофакторный комплекс в Statistica 6)

Цель работы: научиться выполнять многофакторный дисперсионный анализ в программном продукте Statistica 6.