Решение транспортной задачи линейного программирования в матричной постановке
Лабораторная работа № 7
Цель работы:
1) Познакомиться с моделью транспортной задачи линейного программирования.
2) Научиться составлять опорный план различными методами (минимального элемента, Фогеля, северо-западного угла).
3) Научиться получать оптимальное решение методом потенциалов.
Объем работы 2 часа
1.Общие сведения
Сущность транспортной задачи линейного программирования состоит в наивыгоднейшем прикреплении поставщиков однородного продукта ко многим потребителям этого продукта. На практике постоянно возникает необходимость решения таких задач, особенно когда количество пунктов отправления и получения грузов увеличивается.
Условие транспортной задачи обычно записывается в виде матрицы, в которой потребители однородного груза размещаются по столбцам, а поставщики - по строкам. В последнем столбце матрицы проставляют запас груза, имеющийся у каждого поставщика, а в последней строке - потребность в нем потребителей. На пересечении строк со столбцами (в клетках матрицы) записывают расстояние пробега по всем возможным маршрутам, время доставки груза, или затраты на перевозку единицы груза по этим маршрутам.
Математически транспортная задача по критерию стоимости формируется следующим образом. Имеется п потребителей и т поставщиков однородного груза. Мощность i-гo поставщика (i = 1,m) обозначим аi, спрос j-го потребителя (j = 1,п) bj. Затраты на перевозку одной тонны груза от i-гo поставщика до j-го потребителя обозначим сij. Размер поставки продукции поставщиком i потребителю j обозначим хij; общую сумму затрат на перевозку груза обозначим через F.
Запишем математическую модель задачи:
1) объем поставок i-гo поставщика должен равняться количеству имеющегося у него груза:
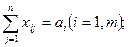
2) объем поставок j-му потребителю должен быть равен его спросу:
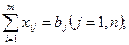
3) запас груза у поставщиков должен равняться суммарному спросу потребителей:
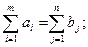
4) размер поставок должен выражаться неотрицательным числом:
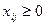
5) общая сумма затрат на перевозку груза должна быть минимальной:
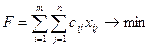
Поставленная в задаче цель может быть достигнута различными методами, например, распределительным методом или методом потенциалов.
Модель транспортной задачи линейного программирования может использоваться для планирования ряда операций, не связанных с перевозкой грузов. Так, с ее помощью решаются задачи по оптимизации размещения производства, топливно-энергетического баланса, планов загрузки оборудования распределения сельскохозяйственных культур по участкам различного плодородия
Построения начального опорного плана
Рассмотрим способы построения начального опорного плана. Составить опорный план можно различными способами. Однако для всех способов непременным является требование, чтобы в процессе заполнения распределительной таблицы в каждую загружаемую клетку вписывалась максимально возможная по величине поставка. В таком случае каждый раз будет либо исчерпываться весь запас груза у поставщика (мы будем говорить: "закрывается строка"), либо полностью удовлетворяться спрос потребителя ("закрывается столбец"). Соблюдение этого требования обеспечит заполнение именно m + n – 1 клеток.
Способ "северо-западного угла".Первой загружается клетка (1; 1). Если закрывается строка, то следующей загружается клетка (2; 1); если же закрывается столбец, то следующей загружается клетка (1; 2). Итак, каждый раз загружается клетка, соседняя либо по строке, либо по столбцу (в зависимости от конкретных данных задачи). Последней будет загружена клетка (т; п). В результате загруженные клетки расположатся вдоль диагонали (1; 1) — (т; п), поэтому способ "северо-западного угла" называют еще диагональным способом.
Существенным недостатком способа "северо-западного угла" является игнорирование при загрузке клеток тарифов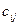 
, поэтому построенный опорный план обычно оказывается весьма далеким от оптимального.
Способ "минимального элемента". Первой в распределительной таблице загружается клетка с наименьшим тарифом. Далее загружается клетка той же строки (столбца) со следующим по величине тарифом и т. д.
Поскольку при заполнении таблицы учитываются величины тарифов, то, как правило, построенный план оказывается ближе к оптимальному, нежели построенный способом "северо-западного угла".