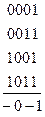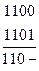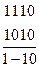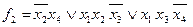Тупиковой ДНФ называется дизъюнкция всех импликант, составляющих приведенную систему.
Тупиковая ДНФ- выражение, полученное из сокращенной ДНФ, дальнейшее упрощение которого невозможно в рамках ДНФ.
Минимальной ДНФ называется тупиковая ДНФ, состоящая из наименьшего числа букв.
Одна и та же сокращенная ДНФ может иметь несколько тупиковых ДНФ и несколько минимальных ДНФ.
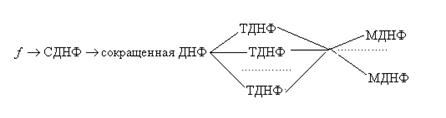
Процесс минимизации на первом этапе сводится к построению полной системы импликант, затем приведенной системы существенных импликант, из которых строится сокращенная ДНФ, затем строятся тупиковые ДНФ и затем уже выбирается минимальная ДНФ. Решение задачи осуществляется в соответствии со схемой
Получение сокращенной ДНФ (нахождение импликантов функции 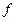 ).
).
Пример 1.
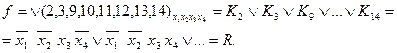
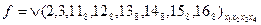
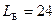
Получение сокращенной ДНФ основывается на законе склеивания 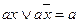 . Из него следует, что можно склеивать или объединять минтермы, отличающиеся только одним сомножителем. Будем склеивать не минтермы, а наборы. Выпишем все наборы переменных, соответствующие минтермам, входящим в разложение функции, в столбик, разбивая их на группы так, чтобы в каждую группу входили наборы с одинаковым числом единиц.
. Из него следует, что можно склеивать или объединять минтермы, отличающиеся только одним сомножителем. Будем склеивать не минтермы, а наборы. Выпишем все наборы переменных, соответствующие минтермам, входящим в разложение функции, в столбик, разбивая их на группы так, чтобы в каждую группу входили наборы с одинаковым числом единиц.
| N Груп пы | Наборы |  набора набора | |||||
| 0010 * | 2 * | 2,3 | 001– * | 2,3, .10,11 | –01– 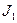 | ||
| 2,10 | –010 * | 2,10, 3,11 | –01– 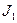 | ||||
| 0011 * | 3 * | 3,11 | –011 * | ||||
| 1001 * | ( 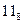 )9 * )9 * | 9,11 | 10–1 | 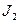 | |||
| 1010 * | 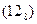 10 * 10 * | 9,13 | 1–01 | 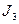 | |||
| 1100 * | ( 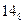 )12 * )12 * | 10,11 | 101– * | ||||
| 10,14 | 1–10 | 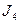 | |||||
| 12,13 | 110– | 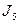 | |||||
| 12,14 | 11–0 | 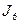 | |||||
| 1011 * | ( 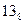 )11 * )11 * | ||||||
| 1101 * | ( 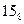 ) 13 * ) 13 * | ||||||
| 1110 * | 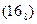 14 * 14 * | ||||||
 Проводим попарное склеивание наборов из соседних групп (для склеивания наборы должны отличаться на одну переменную). При склеивании общие элементы сохраняются, а элементы, которыми различаются наборы, заменяются чертой. Наборы, участвующие в склеивании, помечаются *. В результате образуется второй столбец, к которому также применяется операция склеивания. При этом склеивают наборы из соседних групп с одинаковым положением черточек. Далее образуется 3-й столбец и т.д. Процесс продолжается до тех пор, пока склеивание возможно.
Проводим попарное склеивание наборов из соседних групп (для склеивания наборы должны отличаться на одну переменную). При склеивании общие элементы сохраняются, а элементы, которыми различаются наборы, заменяются чертой. Наборы, участвующие в склеивании, помечаются *. В результате образуется второй столбец, к которому также применяется операция склеивания. При этом склеивают наборы из соседних групп с одинаковым положением черточек. Далее образуется 3-й столбец и т.д. Процесс продолжается до тех пор, пока склеивание возможно.
Импликантами функции 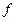 будут наборы во всех столбцах, не участвующие в склеивании (не помеченные).
будут наборы во всех столбцах, не участвующие в склеивании (не помеченные).
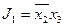 ,
, 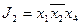 ,
, 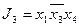 ,
, 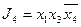 ,
, 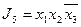 ,
, 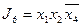 .
.
Сокращенная ДНФ 
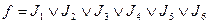 , ее длина составляет 17 букв
, ее длина составляет 17 букв

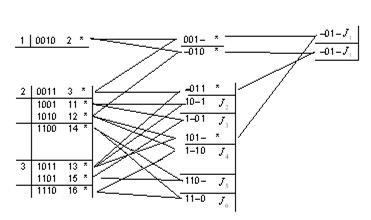
На рис. изображены импликанты и склеиваемые наборы переменных.
Отметим, что на рисунке номера наборов приведены в восьмеричной системе счисления.
2. Следующий этап – построение тупиковой ДНФ. Для этого нужно составить импликантную таблицу. Строки этой таблицы обозначены импликантами функции, а столбцы минтермами функции. Каждая импликанта является частью какого-нибудь дизъюнктивного члена в СДНФ и обращается в единицу на том же наборе, что и соответствующий минтерм. На пересечении строки, в которой записана импликанта, и столбцов соответствующих минтермов, частью которых является импликанта, поставим крестики. Тупиковые формы являются дизъюнкциями тех импликантов, которые накрывают все минтермы, т.е. в таблице нужно выбрать такие строки, чтобы во всех столбцах был как минимум один плюс.
Чтобы построить тупиковую форму, нужно выбрать минимальное число строк, покрывающих крестиками все столбцы. Ясно, что в систему выбранных строк должны обязательно входить строки, содержащие плюсы, которые являются единственными в столбце. Такие строки называются базисными. Простые импликанты, стоящие в базисных строках, образуют ядро рассматриваемой функции. Обведем кружочками плюсы в строках, соответствующих этим импликантам. Из оставшихся импликант выбираем минимальное число таких, которые покрывают крестиками все свободные столбцы (т.е. те, которые не содержат  ).
).
Импликантная таблица
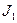 –01– –01– |  | 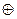 | + | + | ||||
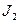 10–1 10–1 | + | + | ||||||
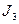 1–01 1–01 | + | + | ||||||
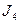 1–10 1–10 | + | + | ||||||
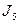 110– 110– | + | + | ||||||
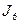 11–0 11–0 | + | + |
В тупиковую ДНФ обязательно должна входить 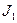 , иначе первые два столбца не накрываются. Следовательно, первая строка является базисной, а импликанта
, иначе первые два столбца не накрываются. Следовательно, первая строка является базисной, а импликанта 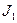 образует ядро функции. При таком выборе автоматически накрываются и еще два столбца . Тупиковыми импликантами являются
образует ядро функции. При таком выборе автоматически накрываются и еще два столбца . Тупиковыми импликантами являются
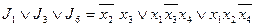 (
(  8)
8)
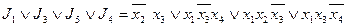 (
(  11)
11)
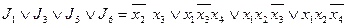 (
(  11)
11)
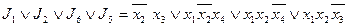 (
(  11)
11)
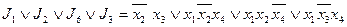 (
( 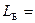 11)
11)
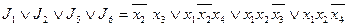 (
( 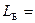 11)
11)
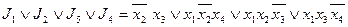 (
(  11)
11)
На рисунке изображены все тупиковые ДНФ:
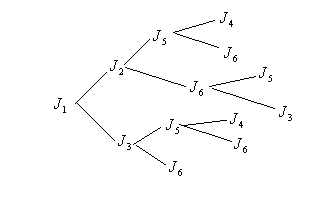
Среди всех тупиковых ДНФ выбираем ДНФ наименьшей длины:
МДНФ: 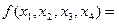
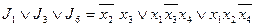
Матричный метод Карно. 
Матричный метод основан на некоторых геометрических построениях. Соотношение между двоичными переменными можно представить в наглядной геометрической форме.
Рассмотрим логическую функцию двух переменных. Все четыре конъюнкции двух двоичных переменных (члены СДНФ) могут быть изображены на плоскости в виде точек с координатами 00,01,10,11, где первая цифра соответствует переменной 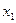 , а вторая – переменной
, а вторая – переменной 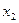 . Эти точки можно соединить линиями и полученный в результате квадрат будет наглядно изображать члены СДНФ двух переменных.
. Эти точки можно соединить линиями и полученный в результате квадрат будет наглядно изображать члены СДНФ двух переменных.
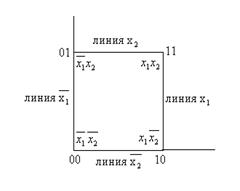
Координаты вершин квадрата, выраженные двоичными числами, соответствуют двоичным номерам конъюнкций.: 00 сответствует 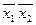 , 01 -
, 01 - 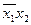 , 10 - , 11 -
, 10 - , 11 - 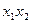 . Координаты соседних вершин отличаются только одним двоичным знаком и, следовательно, минтермы, соответствующие этим числам, отличаются только одной переменной. Если объединить члены, соответствующие двум различным вершинам, то эта переменная будет исключена. Например, сложив минтермы
. Координаты соседних вершин отличаются только одним двоичным знаком и, следовательно, минтермы, соответствующие этим числам, отличаются только одной переменной. Если объединить члены, соответствующие двум различным вершинам, то эта переменная будет исключена. Например, сложив минтермы 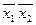 и
и 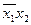 , изображаемые вершинами 00 и 01, получим
, изображаемые вершинами 00 и 01, получим 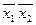
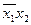 =
= 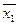 . Ту же операцию исключения переменной можно выполнить, сравнивая непосредственно два двоичных числа 00 и 01.В первом разряде двоичные знаки у обоих чисел одинаковы, поэтому в объединении ставим 0, во втором разряде знаки различны, поэтому во втором разряде ставим черту.
. Ту же операцию исключения переменной можно выполнить, сравнивая непосредственно два двоичных числа 00 и 01.В первом разряде двоичные знаки у обоих чисел одинаковы, поэтому в объединении ставим 0, во втором разряде знаки различны, поэтому во втором разряде ставим черту.
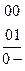
Число 0 соответствует переменной 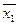 . Черта указывает, что исключена переменная
. Черта указывает, что исключена переменная 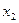 . Следовательно, если два двоичных числа отличаются двоичными цифрами только в одном разряде, то их можно заменить двоичным числом, у которого в этом разряде можно поставить черточку. Черточка указывает номер исключенной переменной. Линия, соединяющая вершины 00 и 01 может быть названа линией
. Следовательно, если два двоичных числа отличаются двоичными цифрами только в одном разряде, то их можно заменить двоичным числом, у которого в этом разряде можно поставить черточку. Черточка указывает номер исключенной переменной. Линия, соединяющая вершины 00 и 01 может быть названа линией 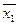 .
.
Геометрической моделью функции трех переменных может служить трехмерный куб, вершины которого соответствуют членам СДНФ. Координаты соседних вершин отличаются, как и в случае плоской модели, только одним двоичным знаком, а соответствующие члены только одной переменной. Вследствие этого линии, соединяющие соседние вершины куба можно обозначить двумя переменными, которые на этой линии не меняют свое значение, а грани куба – одной переменной.
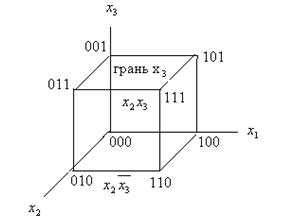
Соединение двух соседних вершин линией позволяет исключить одну переменную, причем это исключение можно выполнить, сравнив двоичные обозначения вершин. Например, сравнивая 011 и 111, получим 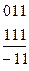 , что соответствует операции сложения конъюнкций
, что соответствует операции сложения конъюнкций 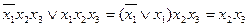
Точно также соединение линиями 4 вершин, лежащих на одной грани, позволяет исключить две переменные. Действительно, сравнив 011 с 111 и 001 с 101, получим
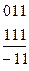
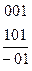
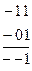
Вначале была исключена переменная 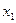 , а затем переменная
, а затем переменная 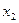 .
.
В результате осталась одна переменная 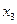 .
.
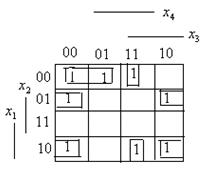
Для функции четырех переменных геометрической моделью является четырехмерный куб. Однако изобразить его на плоскости невозможно и использовать для минимизации сложно. Более удобной для минимизации является карта Карно. Карта Карно построена так, что два соседних столбца (строки) отличаются одним знаком. Любая конъюнкция четырех переменных изображается на карте одной клеткой, находящейся на пересечении строки и столбца, обозначения которых образуют двоичный номер конъюнкции. Конъюнкции, соответствующие соседним клеткам, отличаются только одной переменной. Соседними на карте Карно являются не только клетки, находящиеся внутри карты, но и на концах каждой строки и каждого столбца. Любая функция может быть задана на матрице единицами в клетках, соответствующих входящим в СДНФ конъюнкциям – минтермам, и нулями в остальных клетках, которые можно не записывать. Например, функция 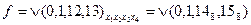 имеет единицы в клетках 0000, 0001,1100, 1101. Четыре минтерма можно сгруппировать по два, объединив для этого соседние минтермы. Объединенные минтермы обводятся замкнутыми линиями. В результате функция приводится к сумме двух конъюнкций трех переменных.
имеет единицы в клетках 0000, 0001,1100, 1101. Четыре минтерма можно сгруппировать по два, объединив для этого соседние минтермы. Объединенные минтермы обводятся замкнутыми линиями. В результате функция приводится к сумме двух конъюнкций трех переменных.
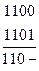
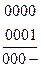
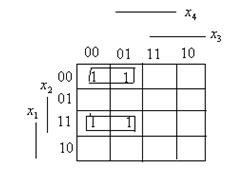
В результате минимизации получим функцию
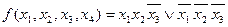 .
.
Преобразования, выполненные на карте Карно, соответствуют следующим алгебраическим преобразованиям
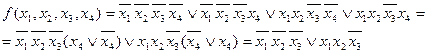 Будем называть конфигурации, образованные соседними заполненными клетками, подквадратами. Подквадрат – набор клеток, в которых одна или несколько переменных имеют постоянное значение. Так, по карте четырех переменных для двухклеточного квадрата характерно то, что в нем три переменные постоянны, а четвертая принимает оба своих значения. Для четырехклеточного подквадрата постоянны две переменные, а две другие принимают все четыре возможные комбинации значений. Объединяя две соседние клетки, мы тем самым будем исключать одну переменную, объединяя четыре соседних клетки, исключаем две переменных, объединяя восемь соседних клеток, - исключаем три переменных. (Это справедливо в том случае, когда форма подквадрата является прямоугольной или квадратной). В подквадраты можно объединять клетки, находящиеся на разных концах строки или столбца.
Будем называть конфигурации, образованные соседними заполненными клетками, подквадратами. Подквадрат – набор клеток, в которых одна или несколько переменных имеют постоянное значение. Так, по карте четырех переменных для двухклеточного квадрата характерно то, что в нем три переменные постоянны, а четвертая принимает оба своих значения. Для четырехклеточного подквадрата постоянны две переменные, а две другие принимают все четыре возможные комбинации значений. Объединяя две соседние клетки, мы тем самым будем исключать одну переменную, объединяя четыре соседних клетки, исключаем две переменных, объединяя восемь соседних клеток, - исключаем три переменных. (Это справедливо в том случае, когда форма подквадрата является прямоугольной или квадратной). В подквадраты можно объединять клетки, находящиеся на разных концах строки или столбца.
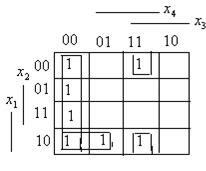
Пример. 2. Пусть функция 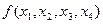 задана картой Карно.
задана картой Карно.
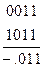
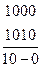

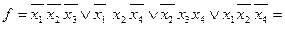
2.. Пусть функция 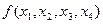 задана картой Карно.
задана картой Карно.
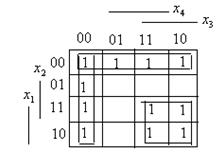
В результате минимизации получится функция
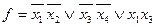
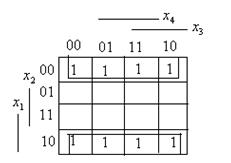
3.. Пусть функция 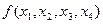 задана картой Карно.
задана картой Карно.
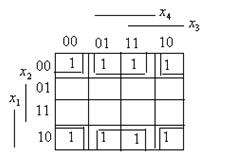
Здесь имеется два четырехклеточных подквадрата.
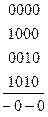
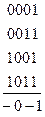
В результате получится функция
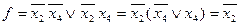
Эту задачу можно решить иначе, если рассматривать один восьмиклеточный подквадрат
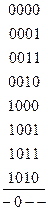 Отсюда сразу получается результат
Отсюда сразу получается результат 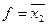 ,
,
Таким образом, задача минимизации сводится к геометрической задаче отыскания правильных конфигураций. При использовании карты Карно нужно стремиться объединить единичные клетки в подквадраты с возможно большим числом клеток, чтобы количество подквадратов было как можно меньше. При решении задачи таким способом могут получиться объединения клеток в одинаковое число подквадратов с одним и тем же числом клеток. Каждый из таких вариантов будет соответствовать одной из минимальных форм функции.
 Следует отметить, что не всегда матричный метод оказывается эффективным. Пусть, например нужно минимизировать функцию
Следует отметить, что не всегда матричный метод оказывается эффективным. Пусть, например нужно минимизировать функцию
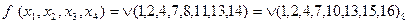
Карта Карно в этом случае имеет вид
Размещение единиц здесь таково, что их нельзя объединить в подквадраты. В то же время функцию легко минимизировать методом Блейка.
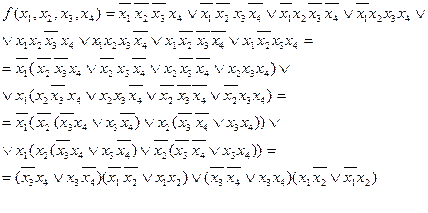
С помощью матрицы Карно можно найти минимальное выражение для функции не только в дизъюнктивной форме, но и в конъюктивной форме. Для этого в карте Карно необходимо выбирать подквадраты из нулей, а не из единиц и помнить о том, что в этом случае 0~x, а 1~ 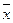 .
.
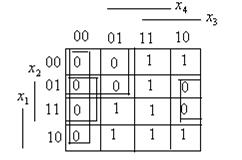
Пример. Найти минимальную функцию в к.н.ф, если 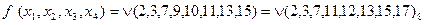 .
.
Составим 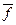 , она содержит в СДНФ конъюнкции, которых нет в СДНФ функции
, она содержит в СДНФ конъюнкции, которых нет в СДНФ функции 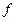 . Они соответствуют тем клеткам матрицы, которых стоит 0
. Они соответствуют тем клеткам матрицы, которых стоит 0
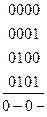 .
. 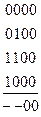
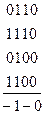
Отсюда получим 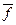 =
= 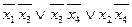 . Найдем теперь отрицание от левой и правой частей этого равенства. В результате получим
. Найдем теперь отрицание от левой и правой частей этого равенства. В результате получим 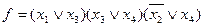
Полученное выражение является минимальной КНФ.
Матричный метод является наиболее эффективным при решении задачи минимизации функций четырех переменных. Для большего числа переменных его использовать затруднительно. При пяти и шести переменных приходится прибегать к некоторым преобразованиям функции для того, чтобы в дальнейшем можно было использовать матричный метод. Например, если имеется функция пяти переменных, то можно вынести за одну скобку некоторую переменную, а за вторую скобку ее отрицание. Тогда внутри скобок окажется функция четырех переменных, которую можно минимизировать матричным методом.
Пример.
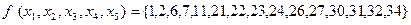
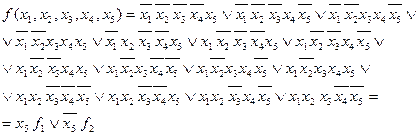
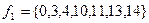
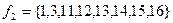
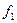
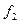
 :
: 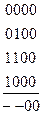
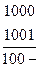
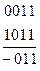
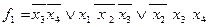
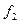 :
: