Распределительный метод решения транспортной задачи

Один из методов решения транспортной задачи – распределительный. Алгоритм этого метода:

1. Для данного базисного распределения поставок подбираем потенциалы строк и столбцов таблицы поставок так, чтобы коэффициенты затрат заполненных клеток стали равными нулю. Составляем матрицу оценок.
2. Если оценки всех свободных клеток неотрицательны, то найденное решение оптимально – решение закончено. Если среди оценок свободных клеток есть отрицательные, то выбираем одну из них для передачи в нее поставки (для определенности можно брать, например, одну из клеток с наименьшей оценкой).
3. Для избранной свободной клетки строится цикл пересчета. Поставка z, передаваемая поциклу, определяется как минимум среди поставок в клетках со знаком «-». Найденная поставка передвигается по циклу. При этом поставка в клетках цикла со знаком «+» увеличивается на z, а в клетках со знаком «-» уменьшается на z. Клетка, поставка в которой при этом станет равной нулю, будет считаться свободной, остальные клетки цикла – заполненными. Таким образом, получено новое базисное распределение поставок.
4. Переходим к пункту 1 алгоритма.

Пример

На заводах А₁,А₂,А₃ производится однородная продукция в количестве а₁,а₂,а₃ единиц. Себестоимость единицы продукции на заводе А_i составляет c_i ден.ед. Четырём потребителям В₁,В₂,В₃,В₄ требуется соответственно b₁,b₂,b₃,b₄ единиц готовой продукции. Расходы c_ij ден.ед. по перевозке единицы готовой продукции с завода А_i потребителю В_j заданы.

Необходимо найти план перевозок, минимизирующий общие затраты по изготовлению продукции на заводах А₁,А₂,А₃ и её доставке потребителям В₁,В₂,В₃,В₄.

Решение

1) Внесём числовые данные транспортной задачи в распределительную таблицу.

Поставщики	Себестоимость ед. продукции	Мощность поставщиков	Потребители и их спрос
b1	b2	b3	b4
А1
А2
А3

Обозначим через x_ij объём перевозок от i-го поставщика к j-му потребителю.

Заданные мощности поставщиков и спросы потребителей накладывают ограничения на значения неизвестных x_ij.

Так как мощность поставщика А_i ограничена а_i, получаем три ограничения по поставщикам:

х₁₁ + х₁₂ + х₁₃ + х₁₄ < 600,

х₂₁ + х₂₂ + х₂₃ + х₂₄ < 400, (1)

х₃₁ + х₃₂ + х₃₃ + х₃₄ < 700.

Аналогично, чтобы спрос каждого из потребителей был удовлетворен, получаем ограничения:

х₁₁ + х₂₁ + х₃₁ > 500,

х₁₂ + х₂₂ + х₃₂ > 300, (2)

х₁₃ + х₂₃ + х₃₃ > 800,

х₁₄ + х₂₄ + х₃₄ > 200.

Очевидно, что объём перевозимого груза не может быть отрицательным, поэтому следует дополнительно предположить, что x_ij > 0; i=1,2,3; j=1,2,3,4.

Суммарные затраты F на перевозку выражаются через коэффициенты затрат и поставки следующим образом:

F = 4х₁₁ + 2х₁₂ + 6х₁₃ + 8х₁₄ + 4х₂₁ + 3х₂₂ + 5х₂₃ + 7х₂₄ + 5х₃₁ + 8х₃₂ + 10х₃₃ + 4х₃₄ (3)

Так как общие затраты на производство продукции постоянны и равны 2*600+4*400+3*700=4900, то общие затраты по изготовлению и доставке продукции равны: f = F + 4900.

Математическая формулировка задачи: на множестве неотрицательных решений системы ограничений (1) и (2) найти такое решение X = (x₁₁, x₁₂ ,…, x₃₃, x₃₄), при котором линейная функция (3) принимает минимальное значение.

2) Так как в нашей задаче суммарный спрос потребителей больше, чем суммарная мощность поставщиков (500 + 300 + 800 + 200 = 1800 > 600 + 400 + 700 = 1700), то это транспортная задача открытого типа.

Для того чтобы привести ее к закрытой, введем "фиктивного поставщика" и в таблицу поставок добавим дополнительную строку. Мощность дополнительного поставщика примем равной 100 = 1800 - 1700. Коэффициенты затрат добавленной строки примем равными нулю.

В итоге системы ограничений (1) – (2) примут вид:

х₁₁ + х₁₂ + х₁₃ + х₁₄ = 600,

х₂₁ + х₂₂ + х₂₃ + х₂₄ = 400,

х₃₁ + х₃₂ + х₃₃ + х₃₄ = 700,

х₄₁ + х₄₂ + х₄₃ + х₄₄ = 100.

х₁₁ + х₂₁ + х₃₁ + х₄₁ = 500,

х₁₂ + х₂₂ + х₃₂ + х₄₂ = 300,

х₁₃ + х₂₃ + х₃₃ + х₄₃ = 800,

х₁₄ + х₂₄ + х₃₄ + х₄₄ = 200.

Целевая функция (3) не изменилась. ТЗ стала закрытого типа.

Построим исходный план перевозок по методу «северо-западного угла». Дадим переменной x₁₁ максимально возможное значение х₁₁ = 500; после этого спрос первого потребителя будет полностью удовлетворен, в результате чего первый столбец таблицы поставок выпадает из последующего рассмотрения (заполненные клетки будем перечеркивать сплошной линией; клетки, выпавшие из последующего рассмотрения, перечеркнуты пунктирной линией).

В таблице поставок найдем новый "северо-западный угол" – клетку (1,2) и дадим в нее максимально возможное значение. Учитывая, что 1 поставщик уже отдал 500 единиц груза, и у него осталось только 100 = 600 - 500 единиц груза, получаем, что х₁₂ = 100. После этого мощность первого поставщика полностью реализована и из рассмотрения выпадает первая строка таблицы поставок. В оставшейся таблице снова находим "северо-западный угол" и т.д. В результате получаем следующее исходное распределение поставок:

Таким образом, исходный план перевозок по методу "северо-западного угла" имеет вид:

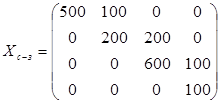
и f(X_c-з) = 4*500 + 2*100 + 3*200 + 5*200 + 10*600 + 4*100 + 0*100 + 4900 = 15100 ден. ед.

Построим исходный план перевозок по методу "минимального элемента".

Просмотрим таблицу тарифов и найдем клетку с минимальным значением тарифа (1,2). В эту клетку запишем максимально возможное значение поставки 300. Так как спрос второго потребителя полностью удовлетворен, второй столбец больше не рассматривается. В оставшейся таблице снова находим клетку с минимальным тарифом (1,1) и в эту клетку записываем максимально возможное значение поставки х₁₁ = 300. После этого мощность первого поставщика исчерпана полностью, и первую строку можно исключить из рассмотрения. В оставшейся таблице найдем клетку с минимальным тарифом (2,1) и запишем поставку х₂₁ = 200 и т.д. В результате получим следующее исходное распределение поставок:

Таким образом, исходный план перевозок по методу "минимального элемента" имеет вид

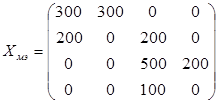
и f(Х_мэ) = 4*300 + 2*300 + 4*200 + 5*200 + 10*500 + 4*200 + 0*100 + 4900 = 14300 ден. ед.

Так как общие затраты меньше для плана Х_мэ на 800 ден.ед., то план Х_мэ лучше.

3) Проверим этот план на оптимальность. Так как на каждом шаге заполнения таблицы по методу "минимальных затрат" возникает одна заполненная клетка, причем из рассмотрения выпадает либо одна строка, либо один столбец, то полученное решение можно принять за базисное.

Базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.

Для того, чтобы найти оценки свободных клеток, надо к коэффициентам затрат таблицы поставок в каждой строке и столбце прибавить такие числа (потенциалы), чтобы коэффициенты затрат в заполненных клетках стали равными нулю. Полученные при этом коэффициенты затрат свободных клеток равны оценкам этих клеток.

Начнем с первого столбца. Пусть потенциал этого столбца равен -4. Рядом с потенциалом в скобках записываем номер шага (поставки опускаем).

После прибавления этого потенциала к коэффициентам затрат первого столбца коэффициенты затрат заполненных клеток (1,1) и (2,1) стали равными нулю; чтобы полученный после сложения коэффициент равнялся нулю, потенциал первой строки должен быть равен 0; для обнуления коэффициента затрат в клетке (2;1) потенциал второй строки должен быть равным 0 и т.д.

				0(2)
				0(3)
				-5(6)
				+5(8)

-4(1) –2(4) –5(5) +1(7)

Измененные коэффициенты затрат удобно выписать в виде отдельной матрицы оценок.

Элементы матрицы оценок, соответствующие свободным клеткам таблицы поставок, равны оценкам этих свободных клеток.

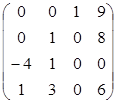
Так как есть клетки с отрицательной оценкой, то распределение поставок не оптимально.

4) Найдем оптимальное распределение поставок с помощью циклов пересчета в распределительной таблице.

Переведем поставку в клетку с наименьшей отрицательной оценкой (3,1). Получаем цикл для этой клетки

(2,1) (2,3)

(3,1) (3,3)

Поставка, передаваемая по циклу, равна x₃₁ = min{500, 200} = 200. Передвигая по циклу поставку, равную 200 единицам, приходим к следующему распределению поставок:

				-4(2)
				0(6)
				-5(4)
				+5(8)

0(1) +2(3) –5(5) +1(7)

Найдем оценки свободных клеток данного распределения

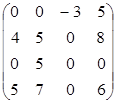
Так как есть клетки с отрицательной оценкой, то распределение поставок не оптимально.

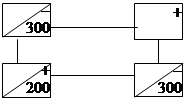
Переведем поставку в клетку (1,3).

Получаем цикл для этой клетки

(1,1) (1,3)

(3,1) (3,3)

Поставка, передаваемая по циклу, равна x₁₃ = min{300, 300} = 300. Передвигая по циклу поставку, равную 300 единицам, приходим к следующему распределению поставок:

				+1
				-4
				+6

–1 –2 –6 0

Найдем оценки свободных клеток данного распределения:

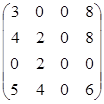
Так как оценки свободных клеток данного распределения неотрицательны, то распределение поставок оптимально. Так как оценка свободной клетки (3,3) равна нулю, то это решение не единственно.

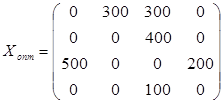
5) Согласно оптимальному плану, с завода А₁ нужно отправить 300 единиц продукции потребителю В₂ и 300 единиц потребителю В₃; с завода А₂ нужно отправить 400 единиц продукции потребителю В₃; с завода А₃ 500 единиц продукции потребителю В₁ и 200 единиц продукции потребителю В₄.

Таким образом, на заводах А₁, А₂, А₃ не останется нераспределенной продукции.

При этом потребитель В₃ не дополучит 100 единиц продукции.

Наименьшие общие затраты на производство продукции и доставку ее потребителям составят

f(Х_опт) = 4900 + 300*2 + 300*6 + 400*5 + 500*5 + 200*4 = 12600 ден.ед.