Уравнение прямолинейной регрессии

Прямолинейная корреляция отличается тем, что при этой форме связи каждому из одинаковых изменений первого признака соответствует вполне определенное и тоже одинаковое в среднем изменение другого признака, связанного с первым или зависящего от первого.

Та величина, на которую в среднем изменяется второй признак, при изменении первого на единицу измерения, называется коэффициентом регрессии. Рассчитывается он по формуле:

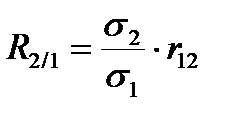, (11.14)

где R_2/1 – коэффициент регрессии второго признака по первому;

s₂ – стандартное отклонение второго признака, который изменяется в связи с изменением первого;

s₁ – стандартное отклонение первого признака, в связи с изменением которого изменяется второй признак;

r₁₂ – коэффициент корреляции между первым и вторым признаками.

Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на отношение сигм:

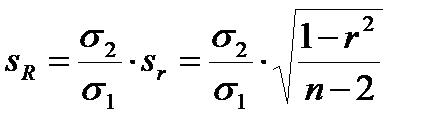(11.15)

Критерий достоверности коэффициента регрессии равен критерию достоверности коэффициента корреляции:

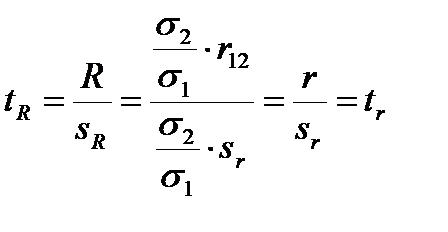, (11.16)

Пример

Для разработки способа определения веса лошадей без взвешивания по обхвату груди было взвешено 1618 лошадей и у каждой из них измерен обхват груди. Получены следующие показатели: х – обхват груди:

n= 1618, μ_х = 174 см, s_x= 7,9 см;

n = 1618, μ_y = 424 кг, s_y = 56,8 кг.

Коэффициент корреляции r_x/y = +0,89 ± 0,011.

Коэффициент регрессии массы по обхвату равен:

.

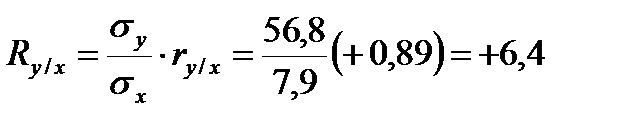Ошибка коэффициента регрессии массы лошадей по обхвату их груди равна:

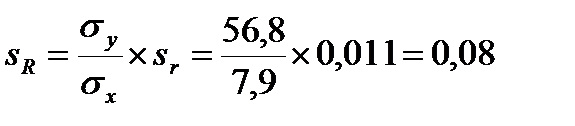
Достоверность этого коэффициента регрессии определяется следующим образом:

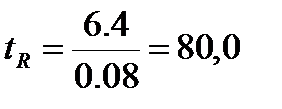, n = 1618–2 =1616, t_st = {2,0 – 2,6 – 3,3}

Возможная максимальная погрешность при прогнозе генерального параметра:

D = t_st × s_R = 2,0 × 0,08 = 0,16.

Доверительные границы:

.

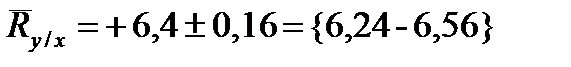Таким образом, можно ожидать, что при увеличении (или уменьшении) обхвата груди на 1 см вес лошадей увеличится (или уменьшится) в среднем на R = 6,4 кг при гарантированном минимуме изменения +6,24 кг и возможном максимуме +6,56 кг, если учитывать изменения признаков в обе стороны от их средней величины.

Коэффициент прямолинейной регрессии показывает, на сколько от своей средней отклоняется второй признак, если первый признак от своей средней отклонился на единицу измерения. Это можно выразить следующей формулой:

(X₂ – μ₂) = R_2/1 (X₁ – μ₁) (11.17)

Обозначая X₁ через х, X₂ через у, R_1/2 через b и произведя необходимые преобразования этого выражения, можно получить рабочую формулу прямолинейной регрессии:

y=a+bx (11.18)

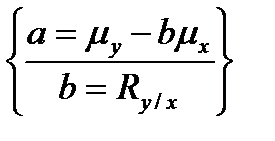. (11.19)

По этой формуле, зная значение х (аргумент), можно определить значение у (функция) без непосредственного его измерения: нужно аргумент х помножить на коэффициент регрессии и к полученному произведению прибавить (или отнять) свободный член а.

Для предыдущего примера (определение веса лошадей по обхвату груди) уравнение регрессии может быть выведено следующим образом:

а = μ_у–R_y/x×μ_x = 424–(+ 6,4) 174 = – 690,

b = R_y/x = + 6,4,

у = а + bх = –690 + 6,4x.

Следовательно, чтобы определить (без взвешивания живой вес лошади по этому способу, надо обхват груди лошади умножить на постоянный коэффициент 6,4 и из полученного произведения вычесть постоянное число – 690.

На основе уравнения прямолинейной регрессии можно заранее рассчитать значение функции для каждого значения аргумента.

По обхвату груди можно определить живой вес лошадей.

Если эти цифры нанести на график, по оси абсцисс которого отложить через равные интервалы значения аргумента (обхвата), а по оси ординат — значения функции (веса), то получится номограмма для определения веса лошадей без взвешивания и без вычислений.