Якою є ймовірність (р), якщо твердження про підвищення врожаю жита (в середньому на 14,2 ц/га) від внесення мікроелементів є статистично істотним?

Відповіді:

1. р = 0,95 4. р = 0,999

2. р = 0,80 5. р = 0,90.

3. р = 0,99

Задача 3. Чи можна вважати достовірним приріст урожаю пшениці під дією добрива А, якщо у великій серії дослідів було встановлено, що без внесення добрива врожай був 17 ± 2 ц, а з внесенням добрива – 20 ± 6 ц.

Який коефіцієнт потрібно використати?

Відповіді:

1. Приріст достовірний. Коефіцієнт F.

2. Приріст достовірний. Коефіцієнт С_v.

3. Приріст недостовірний. Коефецієнт t.

4. Приріст достовірний. Коефіцієнт t.

5. Приріст недостовірний. Коефіцієнт F.

Задача 4. Доліджувався вплив передпосівного опромінення на-сіння на час достигання помідорів. Висіяно 28 помідорів без попереднього опромінення і 36 помідорів з попереднім опроміненням насіння. Час дозрівання опромінених помідорів прискорився, в середньому, на 21 день при стандартній похибці 7,5 днів.

З якою ймовірністю доведено, що прискорення часу дозрівання опромінених помідорів є статистично істотним?

Відповіді:

1. p=0, 950 4. p=0,750

2. p=0,989 5. p=0,995.

3. p=0,900

Задача 5. За даними попередніх досліджень встановлено, що середня довжина тіла окуня виду А дорівнює 150±7 мм (50 обстежень). Проведені нами 40 вимірів засвідчили, що середня довжина тіла окунів цього самого виду дорівнює 139±5 мм.

Яка ймовірність того, що між нашими й даними інших досліджень є достовірна різниця?

Відповіді:

1. p= 0, 92 4. p=0, 95

2. p=0, 80 5. p=0, 50.

3. p=0, 99

Задача 6. У роботі студента стверджується, що середній вміст вітаміну D в печінці становить 652±18 мкг%, а за науковими даними він становить 710±26 мкг%. В обох випадках проведено по 36 дослідів.

Чому дорівнює коефіцієнт Стьюдента для різниці між даними студента і науковими даними?

Відповіді:

1. t=3,0 4. t=1,8

2. t=2,7 5. t=2,4.

3. t=4,7

Задача 7. Між контрольною і дослідною серією експериментів (в обох серіях поставлено по 50 аналізів) різниця в середніх величинах становить 16 одиниць, а стандартна похибка цієї різниці – 6,7 одиниці.

Яка ймовірність статистичної істотності одержаної різниці між контролем і дослідом?

Відповіді:

1. р=0,95 4. р=0,50

2. р>0,99 5. р=0,90.

3. р=0,98

Задача 8. За даними наукової літератури середня величина біоелектричного потенціалу, відведеного від зорового нерва собаки в темряві (на основі шести дослідів), дорівнює 58±4 мв. В нашому експерименті середня величина потенціалу (на основі такої ж кількості дослідів) становила 53±6 мв.

Чи підтверджують наші дані літературні?

Відповіді:

1. Не підтверджують.

2. Підтверджують.

3. Не підтверджують, але суперечать незначно.

4. Для відповіді на це питання, потрібно продовжити дослід-ження.

5. Дати відповідь на поставлене запитання неможливо.

Задача 9. Між середніми значеннями контрольної та експериментальної серій дослідів простежується різниця в 15,5 одиниці при стандартній похибці цієї різниці 9,2 одиниці.

Який можна зробити висновок про цю різницю, якщо в обох серіях було поставлено по 30 дослідів?

Відповіді:

1. Різниця між контролем та дослідом недостовірна.

2. Різниця між контролем та дослідом визначена помилково.

3. Існує достовірна різниця між контролем та дослідом.

4. Різниця між контролем та дослідом недостатньо гарантована.

5. Нічого конкретного про цю різницю сказати не можна.

Задача 10. За науковими даними добова потреба в білках (у г/кг ваги) різна у хлопчиків і дівчаток і дорівнює відповідно 3,57 ± 0,17 та 1,85 ± 0,35 (n₁ = n ₂ = 20).

Яка ймовірність (p) твердження, що потреба в білках у хлопчиків і дівчаток є різною?

Відповіді:

1. р = 0,99 4. р < 0,50

2. р > 0,999 5. р = 0,90.

3. р = 0,95

Задача 11. Обчислити коефіцієнт Фішера, якщо дисперсія за показником x дорівнює 8,2, а дисперсія за показником y дорівнює 16,4.

Відповіді:

1. F = 1,28 4. F = 2,0

2. F = 12,80 5. F = 20,0.

3. F = 0,20

Задача 12. Чи доведена статистично різниця за мінливістю між показниками x і y (n_x=n_y=20), якщо s_x² =16 і s_y² =48?

Який коефіцієнт потрібно застосувати?

Відповіді:

1. Доведена, коефіцієнт Стьюдента t.

2. Доведена, коефіцієнт варіації C_v.

3. Не доведена, коефіцієнт Стьюдента t.

4. Не доведена, коефіцієнт Фішера F.

5. Доведена, коефіцієнт Фішера F.

Задача 13. У контрольній серії дослідів одержано дані, що вміст вітаміну В₁₂ в рубці корів дорівнює 160±25 мкг%. В умовах ультрафіолетового опромінення корів вміст вітаміну В₁₂ збільшився до 200 ± 40 мкг% (n₁=n₂=10).

Питання 1.Чи достовірне це збільшення, яка його ймовірність? Який коефіцієнт слід застосовувати, відповідаючи на це питання?

Відповіді:

1. Недостовірне, p=0,56. Коефіцієнт Фішера F.

2. Недостовірне, p=0,56. Коефіцієнт.Стьюдента t.

3. Достовірне, p=0,95. Коефіцієнт Стьюдента t.

4. Достовірне, p=0,95 . Коефіцієнт кореляції r.

5. Достовірне, p=0,95. Коефіцієнт Фішера F.

Питання 2. Чи різниця в мінливості між контролем і дослідом є статистично істотною? Який статистичний показник треба застосувати?

Відповіді:

1. Ні. Коефіцієнт Стьюдента t. 4. Так. Коефіцієнт Стьюдента t.

2. Ні. Коефіцієнт Фішера F. 5. Так. Коефіцієнт Фішера F.

3. Ні. Коефіцієнт варіації С_v.

Задача 14. Чи різниця за мінливістю між двома показниками x і y є статистично достовірною (р³0,95), якщо в 20 дослідах одержано такі дані: х – 25±8 од.; y – 42±11 од.

Який коефіцієнт потрібно застосувати?

Відповіді:

1. Так. Коефіцієнт Стьюдента t.

2. Так. Коефіцієнт варіації C_v.

3. Так. Коефіцієнт Фішера F.

4. Ні. Коефіцієнт Фішера F.

5. Ні. Коефіцієнт Стьюдента t.

Задача 15. Встановлено, що кількість цукру в крові зменшується при інтенсивній м’язовій роботі. Так, у нормі вона дорівнює 110 ± 3,2 мг%, а під час спортивних змагань – 70 ± 1,8 мг% (n₁ = n ₂ = 20).

Питання 1. Яка ймовірність статистичної істотності цього зменшення? Який треба застосувати показник, відповідаючи на це запитання?

Відповіді:

1. р = 0,95. Коефіцієнт t. 4. р > 0,999. Коефіцієнт С_v.

2. р = 0,95. Коефіцієнт F. 5. р > 0,999. Коефіцієнт t.

3. р > 0,999. Коефіцієнт F.

Питання 2. Чи можна стверджувати з імовірністю р ≥ 0,95 що різниця в мінливості цукру в крові в нормі і при м’язовій роботі є статистично достовірною?

Відповіді:

1. Так. Коефіцієнт F. 4. Ні. Коефіцієнт t.

2. Так. Коефіцієнт t. 5. Так. Коефіцієнт С_v.

3. Ні. Коефіцієнт t.

2.3. Задачі на обчислення коефіцієнта кореляції та визначення рівняння лінійної регресії для двох взаємозалежних ознак

Задача 1. При дослідженні тісноти взаємозв’язку між явищами х і у одержано коефіцієнт кореляції r = 1,86.

Що можна сказати про тісноту взаємозв’язку між досліджуваними явищами?

Відповіді:

1. Кореляція позитивна і тісна.

2. Кореляція негативна і тісна.

3. Кореляцію не доведено з достатньою достовірністю.

4. При обчисленні коефіцієнта кореляції допущено арифметичну помилку.

5. Кореляція позитивна, але слабка.

Задача 2. При попарному дослідженні взаємозв’язку між низкою показників одержано п’ять різних значень коефіцієнта кореляції.

Який з них засвідчує про на найбільшу тісноту взаємозв’язку між двома досліджуваними показниками?

Відповіді:

1. r = 0,72 r = – 0,95

2. r = 1,25 r = 2,00.

3. r = – 0,87

Задача 3. Досліджувався взаємозв’язок між двома показниками x i y. Коефіцієнти варіації для кожного з них були: C_vx=62%, C_vy=27%.

Чи наявний взаємозв’язок між цими показниками?

Відповіді:

1. Між показниками x і y наявний тісний взаємозв’язок.

2. Між показниками x і y наявний слабкий взаємозв’язок.

3. Для відповіді на поставлене запитання слід продовжити досліди.

4. Обчислені статистичні показники не дають відповіді на поставлене запитання.

5. Взаємозв’язок між двома показниками x і y недостатньо достовірний.

Задача 4. Досліджували, наскільки тісний зв’язок між двома показниками x і y на 12 біологічних об’єктах. Одержано коефіцієнт кореляції r = 0,611.

З якою ймовірністю доведено істотність кореляції між показниками x і y?

Відповіді:

1. р = 0,61 4. р = 0,94

2. р = 0,85 5. р = 0,90.

3. р = 0,96

Задача 5. При дослідженні взаємозв’язку між двома явищами x і y одержано коефіцієнт кореляції r = – 0,8917 на основі 16 аналізів.

Яка ймовірність того, що кореляція між x i y є статистично достовірною?

Відповіді:

1. р = 0,90 4. р = 0,95

2. р > 0,999 5. р = 0,36.

3. р = 0,68

Задача 6. Коефіцієнт кореляції між довжиною тіла і вагою у комах за даними 147 вимірів, становить 0,8692 .

Яка ймовірність його істотності?

Відповіді :

1. Понад p > 0,999 4. p = 0,86

2. Менше p < 0,99 5. p = 0,90.

3. Близько 0,95

Задача 7. Яка ймовірність істотності кореляційного зв’язку між озна-ками a і b, якщо коефіцієнт кореляції між ними, визначений на основі 16 дослідів, дорівнює 0,6527?

Відповіді :

1. p = 0,80 4. p = 0,76

2. p = 0,90 5. p = 0,99.

3. p = 0,95

Задача 8. На основі 120 досліджень зв’язку між довжиною тіла і масою тварин виду А одержано коефіцієнт кореляції r = 0,832.

Чи можна вважати цей зв’язок статистично достовірним, якщо ймовірність висновку р = 0,95?

Відповіді:

1. Так.

2. Мабуть, що так.

3. Треба провести додаткові досліди.

4. Ні.

5. З заданою ймовірністю відповідь дати не можна.

Задача 9. Вивчали взаємозалежність між частотою серцебиття і віком дітей. Було обстежено 12 дітей віком від одного до дванадцяти років. Одержали такі дані:

Вік, роки

Частота серцебиття, уд/хв

Що можна сказати про тісноту і характер кореляційного зв’язку між віком і частотою серцебиття у дітей?

Відповіді:

1. r = 0,09 4. r = 0,98

2. r = – 0,58 5. r = – 0,09.

3. r = – 0,98

Задача 10. Між довжиною тіла x (см) і масою y (г) ховрахів є позитив-на кореляція. Складене рівняння регресії зміни середньої маси у зв’язку із змі-ною довжини тіла має такий вигляд: y=90+3,0(х – 40).

Яке середнє значення y при x=20?

Відповіді:

1. y =10 4. y=40

2. y =20 5. y =50.

3. у=30

Задача 12. Досліджувана група тварин мала середній вік М_x= 60 місяців. Cередня швидкість пульсу у них була М_у =120 уд./хв. Відповідні значення середніх квадратичних відхилень були: 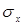= 10, 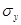= 60. Коефіціент кореляціі між ними r = 0,50.

Яким є рівняння регресії, що засвідчує середню зміну швидкості пульсу від віку (y/x)?

Відповіді:

1. y = 3x–60 4. y = 2x–40

2. y = 3x+60 5. y = 3x–120.

3. y = x–30

Задача 13. Вміст холестерину в крові (х) при захворюванні А на основі 36 визначень становить 260 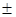25 мг%, а кров`яний тиск (у), відповідно, 180 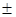20 мм рт.ст., коефіцієнт кореляціі між ними r =0,75.

Як змінюється, в середньому, тиск крові зі зміною вмісту холестерину в крові при захворюванні А?

Відповіді:

1. y = 0,6x+24 4. y = 3,2x–24

2. y = 0,6x+40 5. y = 0,6x–24.

3. y = 3,2x–40

Задача 14. Досліджувався зв`язок між кількістю гемоглобіну в крові (x) і кислотністю шлункового соку (y) у собак. Одержано такі цифрові дані на основі 16 визначень (в умовних одиницях) – середній вміст гемоглобіну х: 85 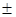11; середня кислотність соку y :162 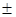45. Коефіцієнт кореляціі між ними: r =0,61.

Скласти рівняння регресіі y/x, яке показувало б як змінюється, в середньому, кислотність шлункового соку зі зміною вмісту гемоглобіну в крові.

Відповіді:

1. y=2,5x-2,5 4. y=2,5x-50

2. y=2,5x+25 5. y=3x-12.

3. y=12x+50

2.4. Задачі на обчислення критерію Пірсонаc²