Кратчайшие пути между всеми парами вершин в орграфе.
Маршрут, но не цепь.
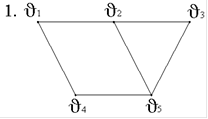
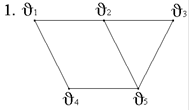
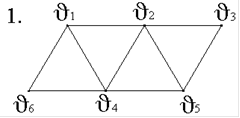
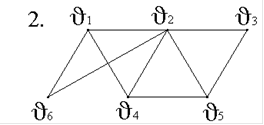
2. Задан граф G(V,E):
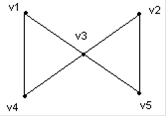
В графе G(V,E) маршрут (v1-v3-v5-v2-v3-v4) - это…
Цепь, но не простая.
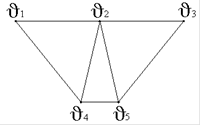
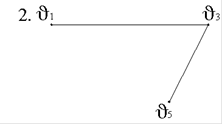
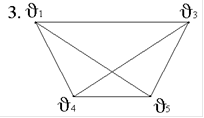
3. Задан граф G(V,E):

В графе G(V,E) маршрут (v1-v4-v3-v2-v5) - это…
Простая цепь.
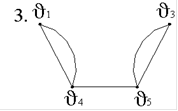
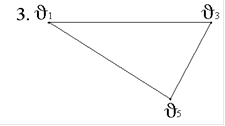
4. Задан граф G(V,E):

В графе G(V,E) маршрут (v1-v3-v5-v2-v3-v4-v1) - это…
Цикл, но не простой цикл.
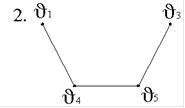
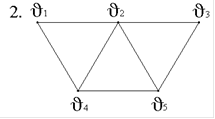
5. Задан граф G(V,E):

В графе G(V,E) маршрут (v1-v3-v4-v1) - это…
Простой цикл.
6. Длина кратчайшей цепи между вершинами u, v (<u,v>) называется…
Расстояние.
7. В графе G(V,E) наибольшая длина из кратчайших путей называется…
Диаметр.
8. Множество вершин, находящихся на одинаковом расстоянии от вершины называется…
Ярус.
9. Полным графом с р вершинами, обозначенным Кр и имеющим максимально возможное число рёбер является…
q(Кр)=p(p-1)/2.
10. Если в орграфе полустепень захода вершины d+(v)=0, то вершина v …
Источник.
11. Если степень вершины равна 1, то вершину называют…
Концевой.
12. Если в орграфе полустепень исхода вершины d-(v)=0, то вершина v …
Сток.
13. Заданы диаграммы графов:
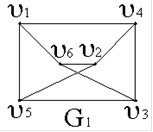

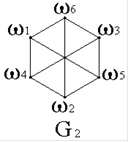

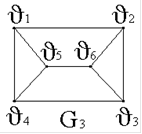
G1,G2.
14. Количество рёбер d(), инцидентных вершине , называется …
Степенью.
15. По теореме Эйлера сумма степеней вершин графа равна:
∑d(q) = 2q.
16. Задан граф G(V1,E1).
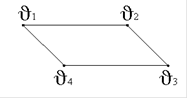
Дополнением G1(V1,E1) является граф …
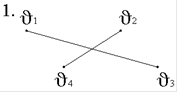
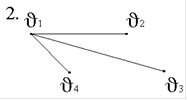
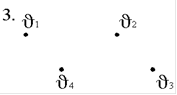
1.
17. Заданы графы G1(V1,E1), G2(V2,E2):
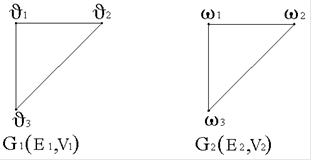
Объединением графов является граф G (V,E): G1(V1,E1) U G2(V2,E2) …
Правильный ответ не указан.
18. Дан граф G1(V1,E1) и граф G2(V2,E2):
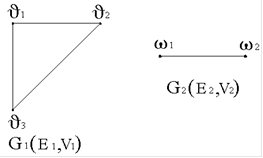
Соединением графов G1 и G2 является граф G(V,E) = G1(V1,E1) + G2(V2,E2) …
3
19. Дан граф G1(V1,E1):
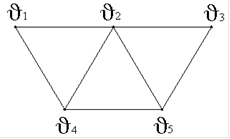
Удаление вершины 2 приводит к графу G(V,E) …
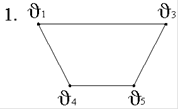
2
20. Дан граф G1(V1,E1):
Удаление ребра (2,4) приводит к графу G(V,E) …
1
21. Добавление ребра е в граф G1(V1,E1) даёт граф G2(V2,E2), где V2:=V1&E2=E1U {e}…
Нет верного ответа.
22. Если степень вершины равна нулю ,d(v)=0, то вершину называют…
Изолированной.
23. Дан граф G(V,E):
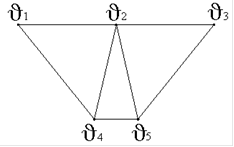
3
24.Дан граф G(V,E):
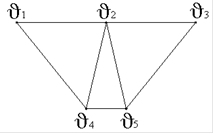
Размножение вершины V графа G1(V1,E1) даёт граф G2(V2,E2), где
V2 := V1 U{'} & E2 := E1 U {(, ')} U { e = (, ')| є F+ ()}
Нет верного ответа.
25. Дан граф G(V,E):
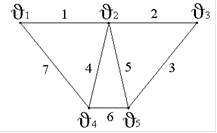
Матрицей смежности вершин является …
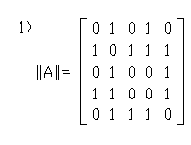
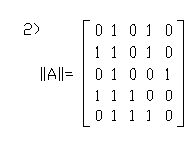
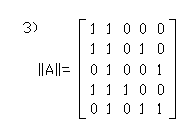
1
26. Матрицей смежности рёбер является …
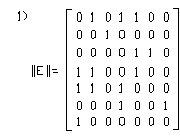
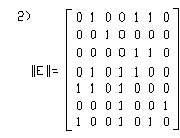
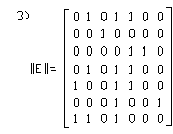
Нет верного ответа.
27. Матрицей инцидентности является …
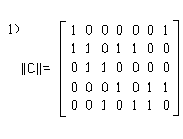
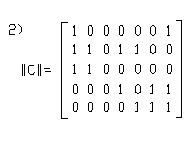
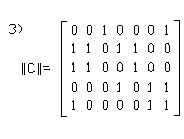
1
28. Если в графе G(V, E) удаление вершины Vi увеличивает число компонент связности, эту вершину называют …
Точка сочленения.
29. Пусть p - число вершин, q - число ребер, k - число компонент связности графов. Тогда справедливы следующие соотношения ...
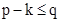
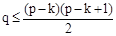
30. Если граф G состоит из одной компоненты связности K(G)= 1, то граф называется ...
Связным графом.
31. Ребро, удаление которого увеличивает число компонент связности, называют ...
Мостом.
32. Связный граф, не имеющий точек сочленения, называют ...
Блоком.
33. Количество рёбер инцидентных вершине v называют степенью d(v) или валентностью, где p - число вершин…
d(v) ≤ р-1.
d(v) ≥ 0.
34. Наименьшее число вершин, удаление которых приводит к несвязному тривиальному графу, называется:
Вершинной связностью.
35. Максимальное количество ресурса, которое может быть передано в единицу времени по заданному ребру, называется ...
Пропускной способностью.
36. Количество ресурса, передаваемого по заданному ребру в единицу времени, называется ...
Потоком по этому ребру.
37. Если граф G несвязный, тогда он имеет следующую характеристику вершинной связности:
λ(G) = 0.
38. Если на сети задан поток x ={xij}<cij, то ребро между вершиной i-й и j-й называется …
Ненасыщенным.
39. Если на сети задан поток x ={xij} и если поток xij по нему совпадает с пропускной способностью, то ребро называется …
Насыщенным.
40. Если задан орграф G (V, E), в котором дуги помечены числами, то эти числа называются …
Весами.
Пропускной способностью.
Длинами.
41. Алгоритм Флойда находит ...
кратчайшие пути между всеми парами вершин в орграфе.
42. Алгоритм Дейкстры находит:
