Сместиться на вектор (5,2)

Прибавь 3

Умножь на 4

Выполняя первую из них, Калькулятор прибавляет к числу на экране 3, а выполняя вторую, умножает его на 4. Запишите порядок команд в программе получения из числа 3 числа 57, содержащей не более 6 команд, указывая лишь номера команд.

(Например, программа 21211 это программа

Умножь на 4

Прибавь 3

Умножь на 4

Прибавь 3

Прибавь 3

которая преобразует число 2 в 50.)

Решение (вариант 1, «прямой ход»):

1) обратим внимание, что в условии ограничено число команд, поэтому неявно ставится задача написать самую короткую программу для решения задачи

2) начнем решать задачу, «отталкиваясь» от начального числа

3) на первом шаге с помощью имеющихся команд из числа 3 можно получить 6 или 12;

4) на втором шаге из 6 можно получить 9 и 12, а из 12 – 15 и 48, и т.д., получается такая схема (структура «дерево»), цифры около стрелок показывает номер выполненной команды:

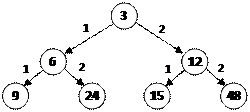
5) уже чувствуется, что дерево сильно разрастается, на следующем уровне будет уже 8 вариантов, потом – 16 и т.д. (на каждом следующем уровне – в 2 раза большем, чем на предыдущем)

6) нужно выбрать такой план дальнейшего перебора вариантов, который может быстрее всего привести к цели (числу 57)

7) видим, что после второй операции ближе всего к результату оказалось число 48, попробуем начать анализ с этой ветки; если не получится – возьмем число 24 и т.д.

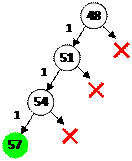
8) ветка дерева, начиная от числа 48, построена на рисунке справа; красный крестик показывает, что полученное значение превышает 57

9) итак, мы вышли на число 57 в результате такой последовательности команд: 22111, ее длина равна 5, что удовлетворяет условию задачи.

10) таким образом, правильный ответ – 22111.

Возможные ловушки и проблемы: · большую схему неудобно рисовать, в ней легко запутаться · не всегда можно сразу угадать нужную ветку «дерева», то есть, ту, которая быстрее всего приведет к успеху

Решение (вариант 2, «обратный ход»):

1) нам нужно увеличить число (с 3 до 57), для этого в большинстве случаев умножение эффективнее сложения, поэтому нужно постараться максимально использовать умножение, а сложение – только в крайних случаях

2) попробуем решить задачу «обратным ходом», начав с числа 57;

3) очевидно, что последней командой не может быть умножение на 4 (57 на 4 не делится), поэтому последняя команда – сложение (прибавь 3), над стрелкой записан номер команды:

4) число 54 также не делится на 4, поэтому предыдущая команда – тоже сложение:

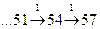
5) аналогично для числа 51:

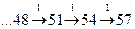
6) число 48 делится на 4, поэтому используем умножение:

7) наконец, добавив в начало программы еще одно умножение, получаем полную цепочку:

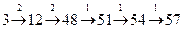
8) таким образом, правильный ответ – 22111, эта программа состоит из 5 команд.

Возможные ловушки и проблемы: · иногда может потребоваться «откат» назад, например, если исходное число – 6, то применив деление на 4 для 12 мы «проскакиваем» его (получаем 12/4=3<6), поэтому нужно возвращаться обратно к 12 и дважды применять сложение; в этом случае ответ будет такой: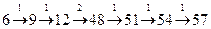

Почему здесь «обратный ход» лучше?: · обратим внимание, что когда мы «шли» в обратном направлении, от конечного числа к начальному, часто очередную операцию удавалось определить однозначно (когда число не делилось на 4) · это связано с тем, что среди допустимых команд есть «не всегда обратимая» операция – умножение: умножить целое число на 4 можно всегда, а разделить нацело – нет; в подобных случаях результат быстрее получается именно «обратным ходом», во время которого сразу отбрасываются невозможные варианты

Еще пример задания:

У исполнителя, который работает с положительными однобайтовыми двоичными числами, две команды, которым присвоены номера:

Сдвинь влево

Вычти 1

Выполняя первую из них, исполнитель сдвигает число на один двоичный разряд влево, а выполняя вторую, вычитает из него 1. Исполнитель начал вычисления с числа 104 и выполнил цепочку команд 11221. Запишите результат в десятичной системе.

Решение:

1) важно, что числа однобайтовые – на число отводится 1 байт или 8 бит

2) главная проблема в этой задаче – разобраться, что такое «сдвиг влево»; так называется операция, при которой все биты числа в ячейке (регистре) сдвигаются на 1 бит влево, в младший бит записывается нуль, а старший бит попадает в специальную ячейку – бит переноса:

?										= 45
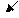										= 90

бит
переноса

можно доказать, что в большинстве случаев результат этой операции – умножение числа на 2, однако есть исключение: если в старшем (7-ом) бите исходного числа x была 1, она будет «выдавлена» в бит переноса, то есть потеряна[1], поэтому мы получим остаток от деления числа 2x на 2⁸=256

3) попутно заметим, что при сдвиге вправо[2] в старший бит записывается 0, а младший «уходит» в бит переноса; это равносильно делению на 2 и отбрасыванию остатка

4) таким образом, фактически команда сдвинь влево означает умножь на 2

5) поэтому последовательность команд 11221 выполняется следующим образом

Код команды	Действие	Результат	Примечание
	умножь на 2
	умножь на 2		остаток от деления 208*2 на 256
	вычти 1
	вычти 1
	умножь на 2		остаток от деления 158*2 на 256

6) правильный ответ – 60.

Еще пример задания:

Исполнитель Робот действует на клетчатой доске, между соседними клетками которой могут стоять стены. Робот передвигается по клеткам доски и может выполнять команды 1 (вверх), 2 (вниз), 3 (вправо) и 4 (влево), переходя на соседнюю клетку в направлении, указанном в скобках. Если в этом направлении между клетками стоит стена, то Робот разрушается. Робот успешно выполнил программу

Какую последовательность из трех команд должен выполнить Робот, чтобы вернуться в ту клетку, где он был перед началом выполнения программы, и не разрушиться вне зависимости от того, какие стены стоят на поле?

Решение:

1) фактически заданная программа движения Робота, которую он успешно выполнил, показывает нам свободный путь, на котором стенок нет

2) поэтому для того, чтобы не разрушиться на обратном пути, Робот должен идти точно по тому же пути в обратном направлении

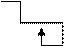
3) нарисуем путь Робота, который выполнил программу 3233241:

?	?	?	?	?	?
?			?	?	?
?	?				?
?	?	?			?
?	?	?	?	?	?

Робот начал движение из клетки, отмеченной красной точкой, и закончил в клетке, где стоит синяя точка

4) чтобы вернуться в исходную клетку (с красной точкой) по пройденному пути, Роботу нужно сделать шаг влево (команда 4), затем шаг вверх (команда 1) и еще один шаг влево (команда 4)

5) таким образом, ответ – 414.

Еще пример задания:

Исполнитель Робот ходит по клеткам бесконечной вертикальной клетчатой доски, переходя по одной из команд вверх, вниз, вправо, влево в соседнюю клетку в указанном направлении. Робот выполнил следующую программу:

Вправо

Вверх

Влево

Влево

Вниз

Вниз

Вправо

Вправо

Вправо

Вниз

Влево

Укажите наименьшее возможное число команд в программе, переводящей Робота из той же начальной клетки в ту же конечную.

Решение (способ 1, моделирование движения Робота):

1) отметим, что в условии ничего не говорится о стенках, то есть, молчаливо предполагаем, что их нет

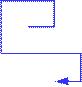
2) можно повторить все движения Робота на бумажке и посмотреть, куда он уйдет; на схеме исходная точка обозначена красной точкой, а конечная – синей, синяя линия показывает путь Робота:

3) поскольку Робот не может ходить по диагонали, для перехода из начальной точки в конечную кратчайшим путем ему нужно выполнить, например, такую программу (см. штриховые линии на рисунке):

вниз вниз вправо

4) есть и другие варианты (попробуйте их найти!), но все они содержат 3 команды: одну команду вправо и две команды вниз

5) таким образом, ответ – 3.

Решение (способ 2, анализ программы):

1) можно решить задачу без повторения движений Робота

2) обратим внимание, что пары команд «вперед-назад» и «влево-вправо» дают нулевой эффект, то есть, не перемещают Робота, поэтому все такие пары можно выкинуть из программы

3) поскольку стенок нет, все равно где стоят парные команды в программе, вычеркиваем их:

вправо

вверх

Влево

Влево

Вниз

Вниз

Вправо

Вправо

вправо

Вниз

Влево

4) смотрим, какие команды остались (они отмечены желтым маркером), их всего 3

5) таким образом, ответ – 3.

Еще пример задания:

Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 0. Система команд Кузнечика:

Вперед 4 – Кузнечик прыгает вперед на 4 единицы,

Назад 3 – Кузнечик прыгает назад на 3 единицы.

Какое наименьшее количество раз должна встретиться в программе команда «Назад 3», чтобы Кузнечик оказался в точке 27?

Решение (составление уравнения, подбор решения):

1) обозначим через 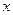количество команд «Вперед 4» в программе, а через 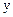– количество команд «Назад 3»

2) для того, чтобы КУЗНЕЧИК попал в точку 27 из точки 0, должно выполняться условие

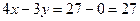
3) это уравнение называется диофантовым; поскольку числа 4 и 3 – взамнопростые (их наибольший общий делитель равен 1), оно имеет бесконечно много решений

4) из всех решений нас интересует такое, при котором – наименьшее возможное неотрицательное (!) число

5) представим уравнение в виде

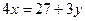
нужно подобрать минимальное неотрицательное , при котором правая часть делится на 4

6) дальше используем метод подбора (или перебора), начиная от 1; получаем

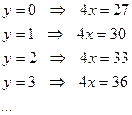
7) видим, что первое , при котором 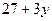делится на 4, это (при этом ).

8) таким образом, ответ – 3.

Задачи для тренировки[3]:

1) У исполнителя Утроитель две команды, которым присвоены номера:

Вычти 2

Умножь на три

Первая из них уменьшает число на экране на 2, вторая – утраивает его. Запишите порядок команд в программе получения из 11 числа 13, содержащей не более 5 команд, указывая лишь номера команд. (Например, 21211 – это программа:

Умножь на три

Вычти 2

Умножь на три

Вычти 2

Вычти 2,

которая преобразует число 2 в 8). (Если таких программ более одной, то запишите любую из них.)

2) У исполнителя Калькулятор две команды, которым присвоены номера:

Прибавь 2

Умножь на 3

Выполняя первую из них, Калькулятор прибавляет к числу на экране 2, а выполняя вторую, утраивает его. Запишите порядок команд в программе получения из 0 числа 28, содержащей не более 6 команд, указывая лишь номера команд. (Например, программа 21211 – это программа:

Умножь на 3

Прибавь 2

Умножь на 3

Прибавь 2

Прибавь 2,

которая преобразует число 1 в 19).

3) У исполнителя УТРОИТЕЛЬ две команды, которым присвоены номера:

Вычти 1

Умножь на 3

Первая из них уменьшает число на экране на 1, вторая – увеличивает его в три раза.

Запишите порядок команд в программе получения из числа 3 числа 16, содержащей не более 5 команд, указывая лишь номера команд.

(Например, программа 21211 это программа

Умножь на 3

Вычти 1

Умножь на 3

Вычти 1

Вычти 1

которая преобразует число 1 в 4.)

4) Имеется исполнитель Кузнечик, который живет на числовой оси. Система команд Кузнечика:

Вперед N (Кузнечик прыгает вперед на N единиц);

Назад M (Кузнечик прыгает назад на M единиц).

Переменные N и M могут принимать любые целые положительные значения. Известно, что Кузнечик выполнил программу из 50 команд, в которой команд “Назад 2” на 12 больше, чем команд “Вперед 3”. Других команд в программе не было. На какую одну команду можно заменить эту программу, чтобы Кузнечик оказался в той же точке, что и после выполнения программы?

5) Исполнитель КАЛЬКУЛЯТОР имеет только две команды, которым присвоены номера:

Умножь на 2

Вычти 2

Выполняя команду номер 1, КАЛЬКУЛЯТОР умножает число на экране на 2, а выполняя

команду номер 2, вычитает из числа на экране 2. Напишите программу, содержащую не

более 5 команд, которая из числа 7 получает число 44. Укажите лишь номера команд.

Например, программа 11221 – это программа:

Умножь на 2;

Умножь на 2;

Вычти 2;

Вычти 2;

Умножь на 2,

которая преобразует число 5 в число 32.

6) Исполнитель КАЛЬКУЛЯТОР имеет только две команды, которым присвоены номера:

Умножь на 3

Вычти 2

Выполняя команду номер 1, КАЛЬКУЛЯТОР умножает число на экране на 3, а выполняя

команду номер 2, вычитает из числа на экране 2. Напишите программу, содержащую не

более 5 команд, которая из числа 1 получает число 23. Укажите лишь номера команд.

Например, программа 11221 – это программа:

Умножь на 3

Умножь на 3

Вычти 2

Вычти 2

Умножь на 3,

которая преобразует число 1 в число 15.

7) Исполнитель КАЛЬКУЛЯТОР имеет только две команды, которым присвоены номера:

Вычти 3

Умножь на 2

Выполняя команду номер1, КАЛЬКУЛЯТОР вычитает из числа на экране 3, а выполняя

команду номер 2, умножает число на экране на 2. Напишите программу, содержащую не

более 5 команд, которая из числа 5 получает число 25. Укажите лишь номера команд.

Например, программа 22221 – это программа:

Умножь на 2

Умножь на 2

Умножь на 2

Умножь на 2

Вычти 3,

которая преобразует число 1 в число 13.

8) Исполнитель КАЛЬКУЛЯТОР имеет только две команды, которым присвоены номера:

Умножь на 2

Вычти 1

Выполняя команду номер 1, КАЛЬКУЛЯТОР умножает число на экране на 2, а выполняя

команду номер 2, вычитает из числа на экране 1. Напишите программу, содержащую не

более 4 команд, которая из числа 7 получает число 52. Укажите лишь номера команд.

Например, программа 12121 - это программа:

Умножь на 2

Вычти 1

Умножь на 2

Вычти 1

Умножь на 2

которая преобразует число 5 в число 34.

9) Исполнитель Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след в виде прямой линии. У исполнителя существуют следующие команды:

Сместиться на вектор (а, Ь) – исполнитель перемещается в точку, в которую можно попасть из данной, пройдя а единиц по горизонтали и b – по вертикали.

Запись: Повторить 5[ Команда 1 Команда 2] означает, что последовательность команд в квадратных скобках повторяется 5 раз.

Чертежник находится в начале координат. Чертежнику дан для исполнения следующий алгоритм:

Сместиться на вектор (5,2)