Расчетные нагрузки и их комбинации. Расчетные нагрузки для металлических конструкций пор­тальных кранов и их расчетные

Расчетные нагрузки для металлических конструкций пор­тальных кранов и их расчетные комбинации приведены в табл. 7.

Примечания к таблице:

1. Комбинации нагрузок предусматривают работу следующих механизмов: Ia и IIa – кран, поворотная часть и стреловое устрой­ство неподвижны, работает механизм подъема; Ib и IIb – кран с грузом, механизмы подъема, вращения и передвижения не ра­ботают, работает механизм изменения вылета; Ic и IIc – кран с грузом, механизмы подъема, изменения вылета и передвижения не работают, работает механизм вращения; Id и IId – кран без груза, поворотная часть и стреловое устройство неподвижны относительно портала, работает механизм передвижения. Кроме трех основных случаев нагрузок могут быть случаи особых нагру­зок (л.10).

2. Коэффициенты динамичности принимаются по табл. 8.

3. Углы отклонения канатов принимаются по табл. 9.

4. Коэффициенты толчков k_т'= 1,1 и k_т= 1,2.

5. P_К, P_ц, P_И, Р_п. При этом при расчетах на сопротивление усталости для P_К, P_И, Р_п пуски и тормо­жения считаются плавными, а при расчетах на прочность от по­стоянных нагрузок принимается резкий пуск (торможение) и t₁≥ 0,5τ, т. е. значения P_И и Р_пнадо считать вдвое большими.

6. P_вIII,определяется по ГОСТ 1451-77.

7. При расчетах на прочность для грейферных кранов по ком­бинации нагрузок IIa вместо Q принимается 1,1Q с учетом воз­можного переполнения грейфера. Для влажных, липких материа­лов рекомендуется принимать 1,25Q.

Для отыскания максимальных нагрузок на отдельные элементы крана необходимо рассмотреть их при различных вылетах и углах поворота в плане. Следует иметь в виду, что отдельные элементы конструкции могут иметь максимальные нагрузки при ненагру­женном кране. Вес портальных кранов G зависит главным образом от грузового момента QR на наибольшем вылете R. С увеличением QR снижается относительное значение веса портальных кранов g = G /(QR)на единицу грузового момента. Так, при QR = 100² кН·м g = 0,4 кН/(кН·м), а при QR = 2500 кН·м g = 0,6 кН/(кН·м) и при дальнейшем уменьшении величины QR g резко возрастает. Качественно такая же закономерность имеет место в отношении веса стрел портальных кранов. Вес порталов составляет 20-30 % от веса портального крана. Здесь больший процент относится к кранам малой, а меньший­ к кранам большой грузоподъемности. Эквивалентная величина груза для расчетов металлических конструкций портальных кpa­нов на сопротивление усталости, по данным ЛЗ ПТО им. С. М. Ки­рова: для крюковых кранов тяжелого режима работы Q_э = 0,85Q, а для грейферных – весьма тяжелого режима работы Q_э = Q. Иссле­дования величин эксплуатационных вылетов R портовых порталь­ных кранов показывают, что зона наиболее вероятных вылетов для груженого крана составляет (0,7÷0,9)R, а для крана без груза ­(0,3÷0,4)R. Грейферные и крюковые тяжелого режима порталь­ные краны следует рассчитывать на неограниченное сопротив­ление усталости, т. е. по числу циклов, равному базовому.

Особенности расчета

Прямые стрелы рассмотрены в гл. 18. Особенностью прямых стрел портальных кранов является то, что в общем случае со стре­лой связаны оттяжные канаты подвижного противовеса и тяга для изменения вылета, усилия в которых изменяются при качании стрелы и определяются при расчете механизма изменения вылета. При качании стрелы изменяются также углы наклона всех дейст­вующих на стрелу сил по отношению к ее продольной оси. Для расчета эти переменные величины удобнее задавать не в табличной, а в графической форме в зависимости от вылета стрелы.

Усилие в подъемных канатах зависит от расчетной комбинации нагрузок (см. табл.7). При угле отклонения канатов α_σ следует рассмотреть случаи отклонений канатов как в сторону наиболь­шего, так и в сторону наименьшего вылета. Вес стрелы G и каса­тельную силу инерции массы стрелы Р_к при пуске или торможе­нии механизма вращения рассматривают либо как распределен­ные по длине стрелы, либо как сосредоточенные силы.

При проверке общей устойчивости стрелы должна быть учтена переменность сечения по длине. Из-за трудности учета совмест­ного действия сжатия и изгиба при переменности поперечного се­чения стрел по длине вместо проверки общей устойчивости следует производить их расчет на прочность по схеме деформированной конструкции с учетом начальных несовершенств.

Расчет шарнирно сочлененных стрел при работе механизма вра­щения рассмотрен. Хобот является балкой на двух опорах. При стреле с гибкой оттяжкой такими опорами являются в плоскости стрелы – стрела и оттяжка, а в плоскости, перпендикулярной к стреле, – две опоры в оголовке стрелы. При стреле с жесткой оттяжкой опорами хобота в обеих плоскостях являются стрела и оттяжка.

В результате исследования хобота шпренгельной конструкции (см. рис. 93) установлено, что ее можно принимать за систему с двумя лишними неизвестными (два шарнирно укрепленных к балке и стойке подкоса) с учетом деформаций, обусловленных изгибающими моментами и нормальными силами (два члена фор­мулы Мора). Расчет хобота следует производить при максималь­ном вылете стрелы. За лишние неизвестные принимаются усилия в подкосах. Расчет в предположении а6солютно жестких узлов при присоединении подкосов к стойке и 6алке дает незначитель­ное уточнение значений напряжений, существенно усложняя рас­чет (шесть лишних неизвестных вместо двух). Учет переменности моментов инерции по длине балки, очень усложняя расчет по сравнению с расчетом в предположении постоянного момента инерции средней величины, уточняет расчетные напряжения незначительно, и этим можно пренебречь. С другой стороны, учет нормальных сил при определении коэффициентов канонических уравнений метода сил заметно уточняет расчетные напряжения и их необходимо учитывать. Так как для расчета хоботов сече­ниями его элементов приходится задаваться, можно делать это на основании предварительного расчета от действия только верти­кальной силы при стреле на максимальном вылете и без учета де­формаций, вызываемых нормальными силами в изгибаемых эле­ментах.

Колонны имеют листовую конструкцию и воспринимают усилия, как в плоскости, так и из плоскости качания стрелы. Расчет производится при крайних и среднем вылетах стрелы.

Расчет металлической конструкции порталов производится по нагрузкам, приведенным в табл. 7. Все нагрузки, передающиеся от поворотной части крана на портал (полупортал), можно свести к следующим системам сил (рис. 95): M_В – момент в вертикаль­ной плоскости, который можно разложить на моменты в плоско­стях вдоль и поперек подкранового пути; Н – горизонтальная сила, которую можно разложить на направления вдоль и поперек подкранового пути; М_г – момент в горизонтальной плоскости; N – вертикальная сила, действующая по оси вращения крана.

Рисунок 96 – Схема к определению опорных давлений портала

Рисунок 95 – Схема сил, действующих на портал

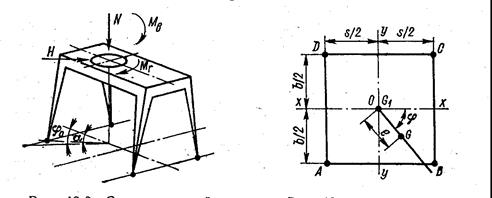
Силы, действующие на портал, уравновешиваются опорными реакциями. Определение давлений при четырех опорах является статически неопределимой задачей, так как имеются только три уравнения статики: ΣV = 0; ΣM_x = 0, ΣM_y = 0. Недостающее четвертое уравнение можно получить исходя из условий дефор­маций. Если предположить портал и его основание абсолютно жесткими, то задача становится статически определимой. Пусть (рис. 96) G – равнодействующая всех вертикальных сил, приложенных к поворотной части крана на расстоянии е,а G₁– вес неповоротной части. Тогда момент Gе разложится на М_х = Gе cos φ и М_у = Gе sin φ и опорные давления будут равны:

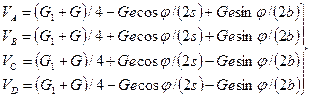(271)

Максимум наибольшего давления на опору В определяется из условия dV_B/dφ = 0, т. е. – sin φ₀ /s + cos φ₀/b = 0, откуда

tg φ₀ = s/b. (272)

В случае, когда угол φ₀ незначительно отличается от угла α(см. рис. 95), в целях упрощения расчетов можно принимать ось стрелы, проходящей через ось ноги портала.

Так как в реальной действительности имеет место суммарная погрешность изготовления портала и неровностей пути h, то при ненагруженной и невесомой конструкции на основание будут опираться только три опоры. Четвертая опора коснется рельса в результате деформации портала, причем при этом произойдет изменение опорных давлений, установленных формулой (271). Исследования показывают, что давление под любой из опор можно определить по формуле

R = R₀ ± ΔR = R₀ ± ch, (273)

где R₀ – опорное давление, определяемое по формулам (271); с – вертикальная жесткость портала с_п и основания с₀, причем

.

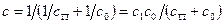Знак «минус» В формуле (273) действителен для двух диаго­нально расположенных опор, под одной из которых имеется за­зор, знак «плюс» – для двух других опор. Опорные давления от действия М_В и N вычисляются по формуле (273); опорные реакции от действия Н вдоль путей – приложенными к тормоз­ным колесам, от действия Н поперек пу­тей – распределенными на четыре опоры, от действия М_г– приложенными к двум по диагонали расположенным опорам и направленными поперек рельсов.

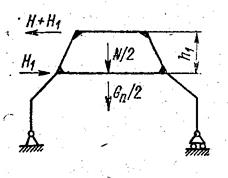
Рисунок 97 – Схема нагружения плоской рамы портала крана с вращающейся колонной

Так как распор, вызванный весом кра­на, исчезнет при перекатывании портала в процессе монтажа, колею портала следует изготовить уже номи­нала на величину деформации ног под действием веса крана. Наибольшая расчетная величина рас­пора Н может быть получена от веса груза, приложенного по оси вращения крана, и вертикальных нагрузок на одну сторону пор­тала, возникающих от действия момента М_В при направлении стрелы вдоль путей. В случае поворота стрелы у неподвижно стоя­щего крана на 180° возможно изменение вертикальных нагрузок на одну сторону портала от суммарного действия моментов, рав­ного 2М_В, что приведет к удвоению величины распора. Распор следует учитывать при комбинациях нагрузок Iа и IIa. Так как при наличии зазоров в ходовых частях величина распора у непод­вижно стоящего крана может уменьшиться практически до нуля, элементы портала, которые разгружаются при действии распора, рассчитываются без его учета.

Портал крана с вращающейся колонной (см. рис. 94, а)пред­ставляет собой пространственную конструкцию, состоящую из двух одинаковых рам, расположенных по диагоналям опорного контура и соединенных между собой в верхней части кольцевым оголовком, в средней – крестовиной и внизу – затяжками.

Момент М_В при положении стрелы вдоль рамы передается на нее в виде двух горизонтальных сил (рис. 97) H₁= M_B/h₁ (вторая рама находится почти под прямым углом к первой и при этом мо­мента М_В не воспринимает). На верхний ригель передается также сила Н (см. рис. 95). Момент М_г вызывает в портале малые на­пряжения, которые можно не учитывать. Сила N передается через опорный подшипник на крестовину и воспринимается поровну двумя рамами. Вес портала G_Π принимается приложенным по его оси.

В этой конструкции портала возможно полное выключение из работы одной из диагональных рам, что должно быть учтено путем условного нагружения диагональной рамы полным вертикальным давлением, действующим на портал, когда при этом он оказывается опирающимся фактически лишь на две опоры. Более опасным для рамы из-за наклона ног является случай отсутствия распора, по­этому рама рассчитывается как внешне статически определимая система. Моменты инерции расчетной рамы на прямых участках принимаются постоянными, равными среднему арифметическому моментов инерции на границах участков у изломов; кольцевой оголовок с моментом инерции сечения относительно горизонталь­ной оси J х в расчетной раме заменяется условной прямой балкой с моментом инерции J_хэк = 2J_x.

Основные преимущества двухстоечных порталов (см. рис. 94, б, в)состоят в меньшей вертикальной жесткости и, сле­довательно, в меньшей чувствительности к неровностям пути и большей технологичности изготовления. По сравнению с порта­лами (см. рис. 94, а)они имеют меньшую себестоимость. Пор­тальные краны должны иметь удобные входы с земли на портал и в кабину, а также к лестницам, расположенным выше портала. Должен быть обеспечен безопасный выход с лестницы портала на площадку, расположенную вокруг оголовка портала, при лю­бом положении поворотной части крана.

СТРЕЛЫ

Типы конструкций

В стреловых кранах, которые должны удовлетворять условиям устойчивости, масса стрел имеет большое значение, так как от нее зависит и масса противовеса. Поэтому стрелам стремятся при­давать форму бруса равного сопротивления. Применение алюминия для крановых конструкций началось со стрел. Шарнирно сочлененные стреловые устройства рассмотрены в л.13, а стрелы, испытывающие изгиб от перемещающегося груза, – в л.13. Стрелы делают листовыми и решетчатыми с прямолинейными и изогнутыми осями с переменным сечением по длине (рис.98). При небольших нагрузках и вылетах встречаются стрелы из одной трубы или из одного коробчатого сечения (рис. 98, а). Стрелы с прямолинейной осью – наиболее легкие и конструктивно простые. Однако они не позволяют на минимальном вылете так высоко поднимать громоздкие грузы, как в случае стрел с изогнутой осью. Недостатками стрел с изогнутой осью являются скручивание их от действия горизонтальных сил и изгиб.

Плоские стрелы применяются при таких типоразмерах, когда их гибкость может быть обеспечена в необходимых пределах (λ ≤ [λ]) и когда из условий устойчивости пояса стрелы не получаются чрезмерно тяжелыми. При этом рациональны трубчатые или коробчатые пояса, соединенные между собой стойками, а также пояса овального сечения, сваренные из гнутых профилей (рис. 98, б). Рациональность такой конструкции объясняется тем, что в горизонтальной плоскости длина l₀, на которой возможно выпучивание, может быть достаточно малой, а в вертикальной плоскости стрела может терять устойчивость на полной длине. В остальных случаях применяют пространственные решетчатые или листовые стрелы прямоугольного или треугольного сечения. Известные преимущества листовых конструкций привели к уменьшению применения решетчатых конструкций для стрел.

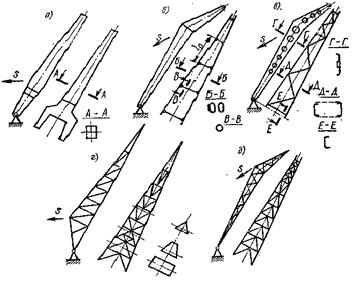
Рисунок 98 – Типы конструкций крановых стрел

В решетчатых конструкциях распространения схема решетки главных ферм стрелы состоит из раскосов, работающих только на растяжение (рис. 98, г). Система решетки горизонтальной фермы часто симметрична относительно продольной оси стрелы (рис. 98, г, д), так как решетка работает во взаимно противоположных направлениях. Поперечные рамы обычно выполняются безраскосными. При постановке в них раскосов применяют симметричные системы: ромбическую, полураскосную и крестовую. Для легко нагруженных стрел большой длины решетчатая конструкция из трубчатых элементов легче, чем из уголковых, вследствие лучшей работы труб на продольный изгиб и уменьшения ветрового давления из-за меньшей величины аэродинамического сопротивления. Применение труб облегчает переход от прямоугольного поперечного сечения стрелы к треугольному (рис. 98, г), которое, как показали исследования, выгоднее. Поскольку в стрелах элементы решетки обычно нагружены слабо, могут оказаться выгодными конструкции с поясами из низколегированных сталей и решеткой из стали 20 (бистальные конструкции). Анализ сечений стрелы для плавучего крана грузоподъемностью 250 т показал, что при трехгранной форме поперечного сечения возможно получить снижение массы на 8 – 10 % по отношению к четырехгранной форме. Стрела оптимальных очертаний по длине будет иметь переменную высоту сечения, уменьшающуюся на концах, и ширину, увеличивающуюся в корне. Если стрела работает на разных вылетах, то оптимальное очертание ее должно быть определено из рассмотрения нескольких вылетов.