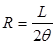Кинематика поворота автомобиля

Существуют следующие способы поворота колесной машины.

1) Поворот передних управляемых колес.

2) Совместный поворот передних и задних управляемых колес.

3) Поворот бортом без управляемых колес за счет отключения передачи вращающего момента на правые или левые неуправляемые колеса и торможение колес, внутренних по отношению к кривой поворота. Поворот без управляющих колес может быть осуществлен созданием разных скоростей вращения колес левого и правого бортов машины (по аналогии с гусеничной машиной).

4) Поворот путем комбинации рассмотренных выше способов.

5) Поворот за счет поворота передней части остова машины при сочлененной раме.

Третий способ поворота (бортом) имеет смысл использовать на машинах со всеми одинакового размера ведущими колесами большого диаметра. При этом упрощается привод к ведущим колесам и компоновка передних колес, однако, повышается износ шин.

На рис.8 схематически показан поворот колесной машины с управляемыми передними колесами (наиболее типичный вариант).

Мгновенный цент поворота О₁ находится в точке пересечения перпендикуляров к векторам скоростей движения колес. Расстояние от центра поворота О₁ до оси заднего моста автомобиля принято называть радиусом поворота R = L·ctg α. При повороте передних управляемых колес машины на одинаковый угол такое пересечение будет невозможно, так как перпендикуляры к векторам скоростей этих колес будут параллельны.

В этом случае движение на повороте сопровождалось бы скольжением управляемых колес вбок, управляемость машины ухудшалась бы, а износ шин и сопротивление движению возросли.

Как следует из рис.8, чистое качение управляемых колес машины без скольжения при движении на криволинейных участках возможно лишь в том случае, если между углами поворота внутреннего θ_в (ближнего к центру поворота) и внешнего θ_н (удаленного от центра поворота) колес будет следующее соотношение:

ctg θ_в = ОС/ВС; ctg θ_н = ОD/АD; разность этих выражений:

,

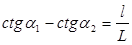где θ_в и θ_н – соответственно углы поворота внутреннего и внешнего управляемых колес;

l – расстояние между осями шкворней поворотных цапф (приближенно может быть принято равным ширине колеи В);

L – база машины.

Выполнение этого условия достигается с помощью шарнирного четырехзвенника, называемого рулевой трапецией, соединяющей между собой управляемые колеса. Подбирая соответствующие значения параметров рулевой трапеции, геометрию элементов и кинематику в целом, получают соотношение между углами θ_в и θ_н , близкое к теоретическому. Однако рулевая трапеция не может обеспечить точно заданное (теоретическое) соотношение между углами поворота колес при различных их величинах, в тех пределах, в которых это необходимо на автомобилях.

Отклонение от теоретических значений углов поворота друг от друга тем меньше, чем правильнее выбраны размеры звеньев, составляющих рулевую трапецию.

При крутых поворотах отклонение действительных углов поворота колес от теоретических – наибольшее. Однако и в этом случае по соображениям безопасности (надежности управления) оно не должно превосходить 1,5⁰.

Установим зависимость между радиусом поворота R, базой машины L и углом поворота управляемых колес α. Если пренебречь небольшим отличием углов поворота управляемых колес и считать, что θ_в = θ_н = θ, то, воспользовавшись схемой рис.8, можно записать следующую зависимость:

.

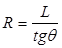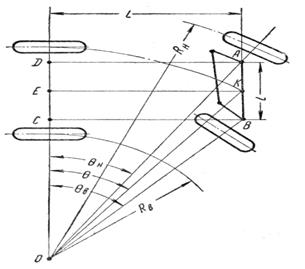
Рис.8. Схема поворота автомобиля с управляемыми передними колесами.

Следовательно, угол поворота колес при движении по кривой определяется радиусом её кривизны. Для малых значений угла α формула примет вид (tg θ ≈ θ):

,

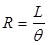где θ - средний угол поворота управляемых колес в радианах.

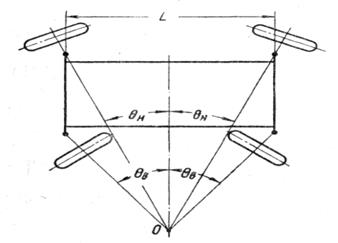
Рис.9. Схема поворота машины с задними и передними управляемыми колесами.

Уменьшение радиуса поворота может быть получено в том случае, если все колеса машины будут управляемы (второй способ поворота), тогда (рис.9):